Gladysheva-tv (1)

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ АЛТАЙСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ им. И. И. ПОЛЗУНОВА

И.Ю.Гладышева, И.П.Мурзина, Т.М. Степанюк

ТЕОРИЯ ВЕРОЯТНОСТЕЙ

Учебно-методическое пособие

Барнаул 2013

1

УДК 519.21(075.5)

Гладышева И.Ю., Мурзина И.П., Cтепанюк Т.М. Теория вероятностей. Учебнометодическое пособие для студентов технических специальностей / Алт. гос. техн. ун-т им. И.И.Ползунова. – Барнаул: 2013. – 98с.

Пособие включает в себя три раздела: Случайные события, Дискретные случайные величины и Непрерывные случайные величины.

Каждый раздел содержит необходимый теоретический материал, сопровождаемый примерами решения задач, и варианты индивидуальных заданий для самостоятельного решения. Задания удобны для рейтинговой оценки знаний студентов. Подобраны равносильные варианты задач, при этом в большинстве задач отсутствует стереотипность формулировок и решений. Приводится список контрольных вопросов по каждой теме для проверки теоретических знаний. Для более глубокого изучения материала приведён список литературы. Примерные варианты контрольных работ (с ответами) дают возможность произвести самоконтроль.

Пособие рассмотрено и одобрено на заседании кафедры высшей математики и математического моделирования.

Рецензент: Е.М.Жданова (к.ф.-м.н, доцент кафедры информационных технологий ААЭП)

2

Оглавление

3

Если при каждой реализации комплекса условий S, когда происходит событие A, происхо-

дит и событие B, то будем говорить, что A влечёт за собой B, и обозначать этот факт или

.

События A1, A2 ,K, An называются несовместными, если в результате одного опыта никакие два из них не могут произойти одновременно:

Примером полной группы несовместных событий является пространство элементарных событий. Другой характерный пример – пара двух противоположных событий: и . Например, выпадение герба и решки при однократном подбрасывании монеты, работоспособность компьютера и его неисправность в данный момент времени, попадание и непопадание в мишень при одном выстреле и т.д.

1.1. В урне 4 красных и 6 белых шаров. Все они пронумерованы от 1 до 10. Урны берут наудачу 1 шар. Событие – шар с чётным номером – обозначим через A, с номером, кратным 3, – через B, шар красного цвета – через C и шар белого цвета – через D. что представляют собой следующие события:

1.3. При каких условиях справедливы следующие соотношения:

1.4. Установите, какие из следующих соотношений верны:

1.6. На контрольной работе было 3 задачи. Событие – студент решил 1-ую задачу – обозначим через A, решил 2-ую задачу – через B и решил 3-ю задачу – через C. Найти выражения для следующих событий:

а) студент решил только 1-ую задачу; б) решил только одну задачу; в) решил только две задачи; г) решил все задачи;

д) решил, по крайней мере, одну задачу; е) решил не более двух задач.

1.2 Относительная частота и вероятность события

Пусть комплекс условий S воспроизводится n раз, причём событие A наступает m раз. Число m называется частотой события A, а число wn (A) = mn называется относительной частотой

события A при этих испытаниях.

Оказывается, что при n → ∞ относительная частота mn колеблется около некоторой посто-

янной P(A) , называемой вероятностью события A. Тогда относительную частоту можно рас-

сматривать как приближённое значение вероятности: P(A) ≈ mn .

События A1, A2 ,K, An называются равновозможными, если при данном комплексе условий S каждое из них имеет одинаковую возможность наступить.

Пусть пространство элементарных исходов Ω состоит из n равновозможных несовместных

n

событий A1, A2 ,K, An ( Ω = ∑Ai ). Исходы, в которых наступает событие A, называются благо-

i =1

приятствующими появлению события A.

Определение. Отношение числа m исходов, благоприятствующих появлению события A, к числу n всех равновозможных исходов опыта называется вероятностью события A:

Формула (1.1) называется классическим определением вероятности. Числовая функция

Пример 1.3. Из 5000 взятых наугад деталей 43 оказались бракованными. Найти относительную частоту бракованных деталей в данной партии.

Решение. В данной задаче событие A – появление бракованной детали. Произведено 5000 испытаний, причём событие A наступило 43раза. Поэтому искомая относитель-

ная частота

43

5000 0,0086.

6

Пример 1.4. В урне 2 белых, 3 зелёных и 5 красных шаров, не различимых на ощупь. Наугад вынимают один шар. Какова вероятность, что он красный?

1.3 Методы комбинаторики

Комбинаторика изучает количества комбинаций, подчинённых определённым условиям, которые можно составить из элементов, безразлично какой природы, заданного конечного множества. Пусть требуется выполнить одно за другим k действий. Если первое действие можно выполнить n1 способами, второе – n2 способами, третье – n3 способами и так до k-го дейст-

вия, которое можно выполнить nk способами, то все k действий можно выполнить n1 n2 K nk способами.

Рассмотрим опыт, состоящий в выборе наудачу одного за другим m шаров из n пронумерованных шаров, содержащихся в урне. Этот опыт будем называть выборкой с возвращением, если после каждого извлечения шар возвращается обратно и, следовательно, может участвовать в дальнейшем отборе. В противном случае мы имеем выборку без возвращения. Номера выбранных шаров образуют множество, состоящее из m натуральных чисел. Если важен порядок следования этих чисел в процессе отбора, то полученное множество называется упорядоченным. В противном случае – неупорядоченным.

Если из n пронумерованных шаров выбирают m с возвращением, то различных упорядоченных выборок будет nm . Если осуществляется выбор без возвращения, то при этом упорядоченное множество называется размещением из n элементов по m, их число обозначают Anm :

Пример 1.6. Наудачу взятый телефонный номер состоит из 6 цифр. Как велика вероятность, что в нём:

а) все цифры различные; б) все цифры нечётные?

Решение. а) На первом месте в шестизначном телефонном номере может стоять любая из цифр: 1, 2, 3, 4, 5, 6, 7, 8, 9, а на всех остальных местах может стоять любая из этих же цифр или ноль. Поэтому всего шестизначных номеров 9 · 10 (выборка с возвращением). Число номеров, у которых все цифры различные, найдем с помощью размещений. При этом учтём, что первая цифра в шестизначном телефонном номере не может быть нулём:

один напротив другого стоят два дивана, на каждом из которых по пять мест. Из десяти пассажиров четверо желают сидеть лицом к электровозу, а трое – спиной к нему. Чему равна вероятность, что данные два пассажира, которым безразлично, где сидеть, окажутся рядом?

Решение. Сначала найдем число всех возможных размещений пассажиров в купе. Пусть A, B, C – пассажиры, которым безразлично, где сидеть. Если A сядет лицом к электровозу, то на диване вместе с ним еще четверо пассажиров могут сесть 5! Способами (перестановки из пяти элементов). Остальные пассажиры на противоположном диване также могут сесть 5! Способами. Таким образом, если A выбрал первый диван, то все пассажиры могут сесть (5!)2 способами. Такое же число способов мы получим, если на первом диване будет не A, а B или C. Тогда число всех равновозможных исходов 3(5!)2.

Благоприятствовать наступлению интересующего нас события будут исходы, когда данные два пассажира, например A и B, будут сидеть рядом. Это возможно, только если A и B сидят спиной к электровозу. Таких случаев будет 5!·3!·2·4. поэтому искомая вероятность

1.7.Французский естествоиспытатель XVIII в. Ж. Л. Бюффон при экспериментальной проверке закона больших чисел подбросил монету 4040 раз, в результате чего герб выпал 2048 раз. Найти относительную частоту выпадения герба в данном эксперименте. (0,5069.)

1.8.Относительная частота родившихся мальчиков среди 2000 новорожденных равна 0,516. Сколько всего мальчиков? (1032.)

1.9.Считая выпадение любой из граней игральной кости одинаково вероятным, найти вероятность выпадения грани: а) с чётным числом очков; б) с числом очков, кратным трём. (а) 0,5;

б) 1/3.)

1.10.Какова вероятность, что в марте наугад названного года окажется 4 воскресенья? (4/7)

1.11.Из партии, в которой 32 детали без дефекта и 6 с дефектом, наудачу взяли 3 детали. Чему равны вероятности следующих событий: а) все 3 детали без дефекта; б) по крайней мере одна деталь без дефекта? (а) 65/124; б) 247/248.)

1.12.Брошены две игральные кости. Чему равна вероятность того, что: а) произведение выпавших очков окажется равным 12; б) сумма выпавших очков не меньше 7; в) произведение выпавших очков равно 12, а сумма равна 7? (. а) 1/9; б) 7/12; в) 1/18.)

8

1.13.Среди кандидатов в студенческий совет 3 первокурсника, 6 второкурсников и 7 третьекурсников. Из этого состава наугад выбираются 5 человек. Какова вероятность, будут выбраны: а) только второкурсники; б) 1 первокурсник, 2 второкурсника и 3 третьекурсника? (а) 0,0014; б) 0,216.)

1.14.Числа 1, 2, 3, 4, …, 9 записываются в случайном порядке. Какова вероятность, что: а) числа записаны в возрастающем порядке; б) числа 5 и 6 стоят рядом? (1/362880; б) 2/9)

1.15.Наугад названо трёхзначное число. Какова вероятность, что сумма цифр в записи числа не больше трёх? (10/27)

1.4 Геометрическая вероятность

Рассмотрим n-мерное вещественное пространство Rn . Пусть в какую-то ограниченную об-

ласть Ω Rn наудачу брошена точка. Слово «наудачу» означает, что все точки области Ω равновозможны. В этом случае вероятность попадания точки в какую-то подобласть A Ω определяется формулой

где m(A), m(Ω) – меры множеств A и Ω соответственно. Мерой m(A) множества A называется его длина l, если A R ; его площадь S, если A R2 и его объём V, если A R3 . В общем случае, если A Rn , то мерой множества называют его n-мерный объём. Элементарными исходами называются точки множества Ω (которое играет роль пространства элементарных исхо-

дов), а благоприятствующими исходами – точки множества A.

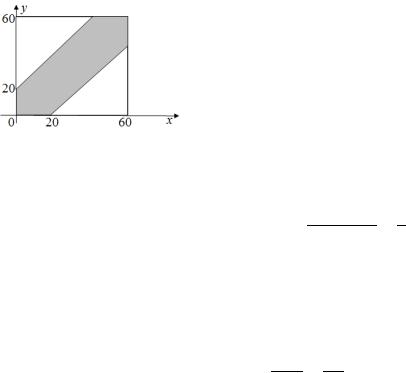
Пример 1.8. (Задача о встрече) Два лица A и B условились встретиться в определённом месте между 12 и 13 часами. Пришедший первым ждёт другого в течение 20 мин, после чего уходит. Чему равна вероятность встречи лиц A и B, если приход каждого из них может про-

единицы масштаба выберем минуту. Всевозможные исходы представляются точками квадрата со стороной 60, а благоприятствующие встрече – располагаются в заштри-

хованной области.

Рисунок 1.1 Искомая вероятность равна отношению площади заштрихованной фигуры к площади всего

в интервал (1,5;2,6)?

Решение. Здесь пространство элементарных исходов весь отрезок Ω=[1;3], а множество благоприятствующих исходов A=(1,5;2,6), при этом длины этих интервалов равны l(Ω)=2 и l(A)=1,1. Поэтому вероятность попадания брошенной точки в указанный интервал равна

1,1 Ω 2 0,55.

9

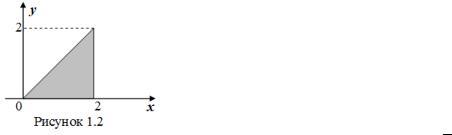
Пример 1.10. На отрезок [0;2] брошены наудачу поочерёдно две точки. Какова вероятность, что первая точка лежит правее второй точки?

Решение. Обозначим координаты точек через x и y. Элементарным исходом при таком бросании будет пара (x,y), а пространством элементарных исходов –

1.16.Два лица условились встретиться в определенном месте между 18 и 19 часами и договорились, что пришедший первым ожидает второго в течение 15 мин., после чего уходит. Найти вероятность их встречи, если приход каждого в течение указанного времени может произойти в любое время, и моменты прихода независимы. (0,4375)

1.17.Какова вероятность, что наудачу брошенная в круг точка окажется внутри вписанного

вкруг квадрата? (2/π≈0,637)

1.18.В шар вписан куб. Какова вероятность, что выбранная наугад внутри шара точка окажется внутри квадрата? (1,48)

1.19.Наугад названы два положительных числа, каждое из которых не превосходит едини-

цы. Какова вероятность, что их сумма больше единицы, а произведение не более 0,5? (≈0,35) 1.20. Наугад названы два положительных числа x и y, каждое из которых не превосходит

двух. Какова вероятность, что произведение xy не больше единицы, а частное y/x не более двух? (≈0,38)

1.5 Теоремы сложения и умножения вероятностей

Теорема сложения. Вероятность суммы двух совместных событий равна сумме вероятностей этих событий за вычетом вероятности произведения этих событий:

Пример 1.11. Найти вероятность того, что наудачу взятое двузначное число кратно либо 2, либо 3, либо тому и другому одновременно.

Решение. Рассмотрим события: A={ число кратно 2}, В={число кратно 3}. Нужно найти

. Т.к. A и B – события совместные, то

10