Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Алтайский государственный технический университет им. И.И.Ползунова

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Gladysheva-tv (1)

.pdf

Скачиваний:

Добавлен:

14.02.2015

Размер:

900.71 Кб

Скачать

☆

<<< < Предыдущая 1 2 3 4 56 / 106 7 8 9 10 > Следующая >>>

3.1. Закон распределения случайной величины задан таблицей.

–2

–1

0,1

0,2

0,3

0,1

Найти: а) неизвестную вероятность; б) функцию распределения

и построить её график;

в) математическое ожидание

дисперсию

и среднее квадратичное отклонение

. Чему

3.2. Даны независимые случайные величины

? (

0,1;

1,29;

1,14

равно значение функции распределения,

в точке

)

и .

X	1	2	3
p	0,1	0,3	0,6

Y	–2	–1	0
q	0,6	0,3	0,1

Найти закон распределения суммы								)	,	и произведения					случайных величин				и .
(	,	,		,	,	,	,	)	,	·	,	,	.			.
найти														убедиться, что:
Дискретная случайная величина								1может принимать только 2 значения:										, причём
3.3.2,5,		0,45,			1,5,			1может принимать только 2 значения:										, причём
. Известны					,		,	. Найдите закон распределения этой								случайной вели-
чины, если:				a)	,		,	. Найдите закон распределения этой									и
				b)		0,1,				3,9,			0,09;
(	3,	4	)			0,3,				3,7,			0,21.
3.4.	3,	4
		Вероятность изготовления нестандартного изделия при налаженном технологиче-

ском процессе постоянна и равна 0,1. Для проверки качества изготовляемых изделий отдел технического контроля (ОТК) берет из партии не более 4 деталей. При обнаружении нестандартного изделия вся партия задерживается. Написать закон распределения числа изделий, проверяемых ОТК в каждой партии. Найти математическое ожидание и дисперсию этой слу-

чайной величины. (

3,439,

1,020.)

3.4 Гипергеометрическое распределение

На практике часто встречается ситуация, которая описывается так называемой урновой моделью. Пусть изучаемая совокупность объёма N содержит элементы двух типов: M элементов первого типа и элементов второго типа. Это могут быть изделия, каждое из которых может быть годным или бракованным, семена, каждое из которых может быть всхожим или нет, и т. п. Эксперимент состоит в одновременном случайном отборе из всей совокупности n элементов. Вероятность появления того или иного события описывается следующей схемой: пусть в урне шаров, из них белых и чёрных. Наудачу из урны вынимают n шаров. Найти вероятность, что среди них будет m белых шаров.

Поскольку порядок элементов здесь не важен, число всех возможных выборок объёма n из

N элементов равен числу сочетаний из N по n: CNn =	N !	. Число опытов, которые благо-
	n! (N − n)!

приятны появлению m белых шаров и остальных	чёрных шаров, равно CMm CNn−−mM . Рас-

смотрим сл. в. X – число белых шаров среди n отобранных шаров. Тогда вероятность того, что случайная величина X примет значение m, находится по формуле

	m	n−m
P(X = m) =	CM CN −M		.	(3.8)
		CNn

Про такую случайную величину говорят, что она имеет гипергеометрическое распределение с параметрами , , . Её математическое ожидание и дисперсия определяются формулами

, 1 1 1 .

Пример 3.8. В аквариуме 10 рыбок, из них 3 рыбки золотые. Случайным образом отлавливают 5 рыбок. Составить закон и функцию распределения случайной величины – числа золотых рыбок среди пяти отловленных. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение.

Решение. Сл.в. – число золотых рыбок среди пяти отловленных. Сл.в. принимает значения 0, 1, 2, 3. Найдем вероятности этих значений:

= P( X = 0) =

C30C75

; p

= P( X =1) =

C31C74

105

;

C105

252

C105

252

= P( X = 2) =

C32C73

105

;

p4 = P( X = 3) =

C33C72

C105

252

C105

252

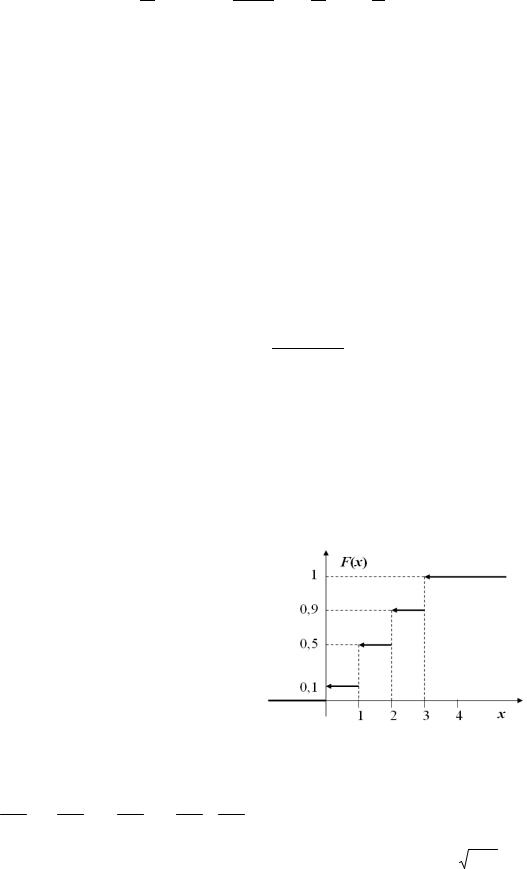
Запишем закон распределения в виде таблицы:

	X	0			1			2		3
	p		21			105			105		21
	p	252			252			252		252
		252			252			252		252
Найдём функцию распределения:
				0			при x ≤ 0,
							при0 < x ≤1,
				21/ 252			при0 < x ≤1,
		F(x) = 126 / 252 при1 < x ≤ 2,

				231/ 252 при2 < x ≤3,
				1			при x >3.

Для удобства построения графика функции распределения запишем рациональные дроби приближёнными десятичными:

0 при x ≤ 0,

0,1 при 0 < x ≤1, F(x) = 0,5 при1 < x ≤ 2,

0,9 при 2 < x ≤ 3,

1 при x > 3.

Рисунок 3.2

Вычислим математическое ожидание, дисперсию и среднее квадратичное отклонение по формулам (2.3), (2.5), (2.7).

MX =0 25221 +1 105252 + 2 105252 +3 25221 = 378252 =1,5.

DX =02	21	+12	105	+ 22	105	+32	21	−(1,5)2	=	714	− 2,25 ≈0,58.	σ = 0,58 ≈ 0,76.
	252		252		252		252			252

							52

3.5 Геометрический закон распределения

Пример 3.9. Производится стрельба по мишени до первого попадания без ограничения

числа выстрелов. Найти закон распределения случайной величины

– числа произведённых

выстрелов, если вероятность попадания при каждом выстреле одна и та же и равна

-ым.

Решение. Сначала найдём вероятность того, что стрельба окончится

выстре-

лом (при первых

выстрелах были промахи, а

-ый выстрел – попадание)1. Так как веро-

ятность произведения независимых событий равна

произведению их вероятностей, то искомая

вероятность

0,1,2,…

·сл.·в. ·

– ·число произведённых,

где

. Тогда

выстрелов – имеет закон

распределения, заданный таблицей:

Это так называемый геометрический закон распределения.

Теорема. Числовые характеристики случайной величины X, имеющей геометрический закон распределения, вычисляются по формулам:

MX =	1	,	DX =	q	.	(2.10)
	p
				p2

3.5. В ящике 2 белых и 3 черных шара. Наудачу извлекают 2 шара а) без возвращения; б) с возвращением. Сл.в. X – число извлечённых белых шаров. Составить закон распределения и

.)	,	.	(а)	0,8,	0,36;б	0,8,
функцию распределения сл.в. X, найти		.	(а)

0,48

3.6. Производится стрельба из орудия по удаленной цели. Вероятность попадания при первом выстреле равна 0,2. При каждом следующем выстреле вероятность увеличивается в 2 раза. Сл.в. X – число попаданий при трех выстрелах. Составить закон распределения, найти ,

,. (MX=1,4; DX=0,56.)

3.7.Студент пришел на зачет, зная 24 вопроса из 30. Преподаватель задает не более 3-х вопросов, но прекращает опрос и выставляет неудовлетворительную оценку, если студент не ответит на 2 вопроса подряд. Сл.в. X – число правильных ответов. Составить закон распределе-

ния, найти	,	. ( MX = 2	183	, DX =	67	.)
			494		120

3.6 Биномиальный закон распределения

Говорят, что дискретная случайная величина Х, принимающая значения 0, 1, 2, …, k, …, n с вероятностями, которые находятся по формуле Бернулли, имеет биномиальный закон распреде-

ления с параметрами n и p.

Пример 3.10. В портфеле компании 3 краткосрочных инвестиционных проекта. Вероятность получения прибыли в первый год работы проекта равна 0,7. Найти распределение случайной величины X – числа проектов, по которым получена прибыль в первый год работы.

Решение. Применим формулу Бернулли.

n =3;

P(X =

0) = P

(0)

=C 0 p0q3−0

= (0,3)3 = 0,027;

p = 0,7 ;

P(X =

1) = P

(1) =C1 p1q3−1 =3 0,7 (0,3)2 = 0,189;

q =1 − p = 0,3;

P(X = 2) = P3 (2) =C32 p2 q3−2 =3 (0,7)2 0,3 = 0,441;

k = 0;1; 2;3.

P( X =

3) = P

(3)

3 p3q3−3 = (0,7)3 = 0,343.

Запишем распределение случайной величины X в таблицу:

0,027

0,189

0,441

0,343

Найдём математическое ожидание и дисперсию биномиально распределённой случайной

величины. Пусть X i

– число наступлений события A в i-том испытании, тогда X = ∑X i , где

X i имеет следующий закон распределения:

i=1

Находим математическое ожидание X:

MX = M

∑X i

= ∑MX i = ∑(0 q +1 p) = ∑p = np .

i=1

Из независимости испытаний следует независимость Xi

, поэтому

DX =D ∑Xi =

∑DXi =∑(MXi2 −(MXi)2) =∑(p − p2) =np (1− p) =npq.

i=1

Таким образом, числовые характеристики биномиального закона

(3.9)

(3.10)

(3.11)

Пример 3.11. Вероятность выигрыша по облигации займа за все время его действия равна 0,1. Некто приобрёл 30 облигаций. Найти математическое ожидание и дисперсию случайной

величины – числа выигравших облигаций среди 30					приобретенных.		30,
Решение.		Сл.в.	Тогда		распределение	с параметрами
0,1.	1	0,6.	имеет биномиальное
			30·0,1	3,	3·0,9	2,7.

Остановимся на происхождении названия «биномиальное распределение». Алгебраическое выражение (q + p)n , где n – натуральное число, называется биномом Ньютона n-й степени. Из школьного курса математики известны биномы Ньютона второй и третьей степени:

(q + p)2 = q 2 + 2qp + p 2 ;

(q + p)3 = q3 + 3q 2 p + 3qp 2 + p3 .

В общем случае бином Ньютона описывается формулой:

(q + p)n =Cn0 qn + C1n qn−1 p + Cn2 qn−2 p2 +... + Cnn−1qpn−1 + Cnn pn .

В соответствии с формулой Бернулли (2.1) заключаем, что

n	n
(q + p)n = ∑Cnk qn−k pk = ∑Pn (k) .
k =0	k =0

Таким образом, вероятности Pn (k) совпадают с членами разложения бинома Ньютона. От-

сюда и происходит название «биномиальное распределение».
Так как для вероятностей q и p верно соотношение	, то и	, т.е. сумма

вероятностей биномиального распределения равна единице:	∑ n	(k) =1. Значит,	1распределе-
	n 1P
ние определено корректно.	k =0

3.8.Отрезок AB длины 15 см разделён точкой C в отношении 2:1. На этот отрезок наудачу брошены 4 точки. Найти вероятность того, что две из них попали левее точки С, а две – правее. (8/27)

3.9.Учебник издан тиражом 100000 экземпляров. Вероятность того, что учебник сброшюрован неправильно, равна 0,0001. Найти математическое ожидание и дисперсию сл.в. X – числа книг без брака.

3.10.Устройство состоит из трёх независимо работающих элементов. Вероятность отказа каждого элемента 0,1. Составить закон распределения сл.в. X – числа отказавших элементов.

Найти 1

3 ,

, . ( 1

0,271,

0,3,

0,21.)

3.7 Непрерывные случайные величины

Определение. Случайная величина называется непрерывной, если её функция распределения имеет вид

где некоторая неотрицательная функция, называемая плотностью распределения вероятностей данной случайной величины.

Теорема. Вероятность любого отдельно взятого значения непрерывной случайной величи-

ны равна нулю.
Доказательство. Покажем, что для любого значения					случайной величины		вероят-
ность	0.
Следствие. Если –		непрерывная случайная величина,			то вероятность попадания		в ин-
Следствие. Если –		∆lim	∆	∆lim	∆	0
тервал ,	не зависит от того, является этот интервал открытым или закрытым, т.е.

Непрерывная случайная величина может принять любое значение из некоторого интервала в отличие от дискретной случайной величины, которая, как указывалось выше, может принимать только отдельные изолированные значения.

Плотность распределения вероятностей обладает следующими свойствами:

1.0;

2.		1;	;	.
3.		1;
4.	если в точке	функция	непрерывна, то

Математическое ожидание		и дисперсия			непрерывной случайной величины опреде-
ляются формулами:			,		.
			,		.
Формула для вычисления дисперсии:					,
где	.				,
Если все значения случайной величины принадлежат интервалу , , то
Пример 3.12. Непрерывная случайная,				величина задана плотностью.распределения вероят-
ностей
			0, если x ≤1,
		f (x) =		А(2x −1), если1 < x ≤ 2,
		f (x) =		А(2x −1), если1 < x ≤ 2,

			0, если x < 2.

Найти: неизвестный параметр A, функцию распределения F(x), математическое ожидание

дисперсию					среднее квадратичное отклонение σ																и вероятность	1	1,5	. По-
строить,	графики плотности,							и функции распределения.														1	1,5
Решение. По свойству 3 плотности
		∞					2											2 = A(4 − 2 −1 +1) = 2A =1 , A=0,5.
		∞					2
		∫ f (x) d x = ∫А(2x −1) d x = A(x2 − x)
		−∞					1											1
		−∞					1		с коэффициентом A=0,5 служит плотностью распределения
Следовательно, функция									с коэффициентом A=0,5 служит плотностью распределения
вероятностей исследуемой случайной величины X, заданной в интервале (1;2).
		x
F(x) =		∫ f (x) d x ,тогда:
при		−∞				0												0.
при	1	1	2			0	и, следовательно,											0.
при							и, следовательно,
		1		1 x					1		2			x			1		2
		1		1 x					1		2			x			1		2
F(x) = ∫0d x +						∫(2x −1) d x =				(x		− x)			=			(x		− x)	;
F(x) = ∫0d x +				2		∫(2x −1) d x =			2	(x		− x)		1	=		2	(x		− x)	;
		−∞		2		1			2					1			2
		−∞				1
при		12		1		2			2				1							2
		12		1		2			2				1			2				2
F(x) = ∫0d x +						∫(2x −1) d x + ∫0d x =								(x			− x)			=1.
F(x) = ∫0d x +				2		∫(2x −1) d x + ∫0d x =							2	(x			− x)			=1.
		−∞		2		1			1				2							1
		−∞				1			1									имеет вид:
Таким образом, функция распределения																		имеет вид:
												0,		если x ≤1,
														2	− x
												x			− x						< x ≤ 2,
									F(x) =									, если 1
									F(x) =					2				, если 1
														2
												1,		если x > 2.

Графики плотности и функции распределения изображены на рис.3.3.

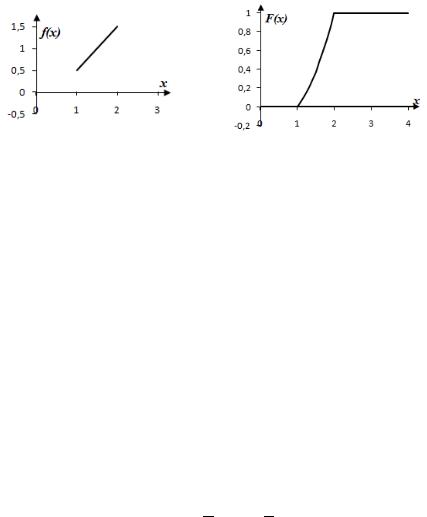
Рисунок 3.3

		b		1 2				1			x3			x2		2			19
		b		1 2				1			x3			x2		2			19

M X = ∫x f (x) dx = 2 ∫x (2 x −1) d x = 2									2	3		− 2						=12			,
		a		1												1
		a		1												1
		b			1	2				1			x4				x3			2	31
		b			1	2				1			x4				x3			2	31
	2	= ∫x	2			∫x	2
M X		= ∫x		f (x)dx =	2	∫x		(2x −1)dx =		2		2 4			−			3			=12 ,
		a				1														1
		a				1														1

D X = M X 2 − (M X )2 =	31	19 2			372				361		11			.
		−		=				−		=
	12	−		=	144			−	144	=	144
	12	12			144				144		144
Вероятность попадания величины1				в		2интервал					1;1,5 :
P(−1 < X <1,5) = F (1,5) − F(−1) =				(1,5		−1,5) − 0 = 0,375 .
P(−1 < X <1,5) = F (1,5) − F(−1) =			2	(1,5		−1,5) − 0 = 0,375 .
3.11. Известна функция распределения сл.в. X:													при		2,
				0			1						при		2,
				0,5			1					2	при 2		2,

1при 2.

Найти: а) вероятность того, что в результате испытания сл.в. X примет значение из интер-

вала		1;1		; б)	, , .	(а) P=1/3; б)		0	0,	при	4,	0,	2	.)	π
вала				; б)		(а) P=1/3; б)								.)
	3.12. Известна плотность распределения сл.в. X:										0					/4,
							2		2	при	0	π/4.				/4,
								0		при		π/4.
	Найти: а) функцию распределения F(x) и вероятность того, что в результате испытания
сл.в. X			.)				0;	π	/12 ; б)		,	.	(а)		P=0,5; б)		π	0,5,
сл.в. X			.)				0;		/12 ; б)		,	.	(а)		P=0,5; б)			0,5,
		примет значение из интервала
	0,5												0,
	0,5
	3.13. Известна плотность распределения сл.в. X:
									5	при
									0	при			0.
	Найти:			1	2 ;	, , .	(		найти		0,04,					)
				1	2 ;	, , .			0,2,		0,04,					0,2

3.8 Мода и медиана. Квантили, процентные точки

Кроме математического ожидания и дисперсии, в теории вероятностей применяется ещё ряд числовых характеристик, отражающих те или иные особенности распределения.

Модой Mo( X ) случайной величины X называется её наиболее вероятное значение (для ко-

торого вероятность pi или плотность распределения f(x) достигает максимума).

Медианой Me( X ) непрерывной случайной величины X называется такое её значение, для которого

P(X < Me(X )) = P(X > Me(X )) =	1	,	(3.12)
	2

т.е. вероятность того, что случайная величина X примет значение, меньшее медианы Me( X ) или большее её, одна и та же и равна 1/ 2 .

Очевидно, что в точке x = Me( X ) функция распределения равна 1/2, т.е. F (Me( X )) =1/ 2 .

F(x)

0,5

0	M e	1	x
	Рисунок 3.4

Если случайная величина X имеет биномиальное распределение, то её мода совпадает с наивероятнейшим числом: Mo(X ) = k0 . Мода и медиана нормально распределённой с парамет-

σ случайной величины равны параметру
рамиПример,	3.13. Найти моду, медиану и математическое.				ожидание случайной величины X с
плотностью распределения f (x) = 3x2			при x [0;1] .
Решение. Очевидно,		что плотность распределения					f (x) = 3x2 максимальна при
x = Mo( X ) =1.
Медиану Me( X ) = b найдём из условия (3.12):
			b	1
			∫ f (x) dx =	1
			∫ f (x) dx =	2
			−∞
или
	b	0	b			b	1
	∫ f (x) dx = ∫		0 dx + ∫3x2 dx = x3			b	1
						0 = b3 =			,
								2
								2
	−∞	−∞	0
откуда	b = Me( X ) = 3 1/ 2 ≈ 0,79 .
Математическое ожидание вычислим по формуле

1	3		1	3

MX = ∫x 3x2 dx =		x4	=		= 0,75 .
	4			4
0			0

Наряду с отмеченными выше числовыми характеристиками случайной величины используются понятия квантилей и процентных точек.

Квантилем уровня q называется такое значение xq непрерывной случайной величины, при котором её функция распределения принимает значение, равное q, т.е.

F (xq ) = P( X < xq ) = q .

(3.13)

Некоторые квантили получили специальные названия. Очевидно, что медиана случайной величины есть квантиль уровня 0,5, т.е. Me( X ) = x0,5 . Квантили x0,25 и x0,75 получили назва-

ние соответственно нижнего и верхнего квантилей.

С понятием квантиля тесно связано понятие процентной точки. Под 100 q процентной точкой подразумевается квантиль x1−q , т.е. такое значение случайной величины X, при кото-

ром P( X ≥ x1−q ) = q .

Пример 3.14. По данным примера 3.18 найти квантиль

x0,3

и 30%-ную точку случайной

величины X.

Решение. Найдём функцию распределения

F(x) = ∫ f (x) d x = ∫0 d x +∫3x2 d x = x3 при x [0;1] .

−∞

Квантиль x

найдём из формулы (3.13): x3 = 0,3, откуда x

≈ 0,67 . 30%-ная точка – это

0,3

квантиль x

. Из уравнения

x3 = 0,7 получаем x

≈ 0,89 .

0,7

3.9 Равномерный закон распределения

Определение: Непрерывная случайная величина

имеет равномерный закон распре-

деления на отрезке

если ее плотность распределения

постоянна на этом отрезке и

равна нулю вне этого отрезка, ,

, если x [a,b],

(3.14)

− a

f (x) = b

если

x [a,b].

Графики плотности

и функции распределения

сл.в.

приведены на рисунке 3.5.

f ( x )

F ( x )

b − a

	b		x		b	x
a				a

Рисунок 3.5 Функция распределения равномерной случайной величины имеет вид:

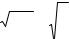
0,	если		х< a,
	− a
x
F(x) =		, если a ≤ x ≤b,		(3.15)
	− a
b			x >b,
1,	если

ее математическое ожидание и дисперсия

MX =	a + b	,	DX =	(b − a)2	.	(3.16)
	2			12

Равномерный закон распределения применяется при анализе ошибок округления, при проведении числовых расчетов, в ряде задач массового обслуживания.

Так, случайная величина , равномерно распределенная на отрезке [0;1] и называемая «случайным числом от 0 до 1», служит исходным материалом для получения случайных величин с любым законом распределения.

Пример 3.15. Поезда метрополитена идут регулярно с интервалом 2 минуты. Пассажир выходит на платформу в случайный момент времени. Какова вероятность того, что ждать пассажиру придется не больше полминуты. Найти математическое ожидание и среднее квадрати-

ческое отклонение случайной величины				времени ожидания поезда.
Решение. Сл. в.			время ожидания поезда – распределена равномерно на отрезке [0;2]
с плотностью f (x) =	1	при	x [ 0;2 ] . Поэтому вероятность того, что пассажиру придется ждать
с плотностью f (x) =		при
2
не более полминуты, равна:
				2	1		x	2		1
				2				2
			P(1,5 <	X < 2) = ∫		dx =			=		.
			P(1,5 <	X < 2) = ∫		dx =			=		.
				1,5	2	2		1,5	4
					2	2		1,5	4

Математическое ожидание, дисперсия и среднее квадратическое отклонение соответственно равны:

MX =	0	+	2	=1	мин, DX =	(2 − 0)	2	=	1	, σ = DX =	1	≈ 0,58	мин.
		2				12			3		3

3.14.Автобус некоторого маршрута идет строго по расписанию с интервалом 5 мин. Сл.в. X

–время ожидания автобуса пассажиром. Найти: а) функцию F(x) и плотность f(x) распределе-

ния; б)	в) вероятность того, что пассажир, подошедший к остановке, будет ожидать не
более двух	,мин;. (	2,5,	25/12, 0	2	0.4.)

3.15.Цена деления шкалы амперметра равна 0,1 А. Показания округляются до ближайшего целого деления. Найти вероятность того, что при отсчете будет сделана ошибка, превышающая

0,02 А. (P(0,02<X<0,08)= 0,5.)

3.16.Случайная величина X распределена равномерно в интервале (5;11). Найти вероят-

ность попадания в интервал

3.10 Нормальный закон распределения

Нормальный закон распределения наиболее часто встречается на практике. Главная его особенность состоит в том, что он является предельным законом, к которому приближаются другие законы при весьма часто встречающихся типичных условиях.

Определение: Непрерывная случайная величина имеет нормальный закон распределения (закон Гаусса) с параметрами и , если плотность распределения имеет вид

<<< < Предыдущая 1 2 3 4 56 / 106 7 8 9 10 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
14.02.2015463.05 Кб108filosofiya_voprosy_s_otvetami.pdf
#
14.02.2015224.77 Кб6Fizicheskaya-kultura-123456-Dlya-vseh-B.doc
#
14.02.20152.12 Mб601FIZIKA-chast-3-2009.docx
#
17.09.20194.03 Mб18FIZIKA-chast-3-2009_-_kopia.doc
#
14.02.20152.21 Mб9FNP.doc
#
14.02.2015900.71 Кб85Gladysheva-tv (1).pdf
#
13.11.2019982.53 Кб29Glava_1.doc
#
13.11.2019837.12 Кб9Glava_4.doc
#
11.11.201932.26 Кб2Great Britain.doc
#
14.02.2015667.99 Кб193Gurova_TIZ.pdf
#
14.02.20151.71 Mб36hrestom-filos.pdf