
Gladysheva-tv (1)
.pdf
.
Двузначные числа – это 10, 11, …, 98, 99. Всего их 90. Очевидно, что 45 из них кратны 2 (благоприятствуют наступлению события A), 30 кратны 3 (благоприятствуют наступлению события B), 15 кратны 2 и 3 одновременно (благоприятствуют наступлению события AB). Поэтому
45 |
1 |
, |
30 |
1 |
, |
15 |
1 |
90 |
2 |
90 |
3 |
90 |
6 |
и, следовательно,
1 1 1 4 2
23 6 6 3.
Вероятность события B, найденная при условии, что событие A произошло, называется условной B и обозначается .
Теорема умножения вероятностей. Вероятность произведения двух событий равна произведению вероятности одного из этих событий на условную вероятность другого при условии, что первое произошло:
Если |
, то говорят, что событие A не зависит от. |
события B. Свойство незави- |
||||||||||||
симости событий взаимное: если |
, то и |
|
|
|
|
|
. |
|
|
|
|
|
|
|
Теорему можно распространить на произведение n событий: |
|
|
|
|
|
|
|
|||||||
|
P(A1 A 2 K An) =P(A1) PA |
(A2) PA A |
(A3) K PA A |
KA |
(An) . |
(1.7) |
||||||||
|
|
1 |
1 2 |
|
1 |
2 |
n−1 |
|
|
|||||
Для независимых событий A и B теорема умножения записывается так: |
|
|
||||||||||||
Для n событий |
, ,…, , независимых в совокупности. |
имеем: |
|
. |
|
(1.8) |
||||||||
Вероятность «хотя бы одного· |
события». Если события |
· …· |
|
независимы в сово- |
||||||||||
· …· |
|
|
|
|
,…, |
|
|
|||||||
формуле |
|
|
|
|
|
|
|
, |
|
|
вычисляется по |
|||
купности, то вероятность появления хотя бы одного из событий, |
,…, |
|
|
|||||||||||
|
P(A1 + A2 +K+ An ) =1 − P( |
|
|
|
|
|
|
|
(1.9) |
|||||
|
A1) P(A2 ) K P(An ) . |
|
||||||||||||
Пример 1.12. В ящике 6 деталей, среди которых 4 стандартных и 2 бракованных. Поочередно из него извлекается по одной детали (с возвращением и без возвращения). Найти условную вероятность извлечения во второй раз стандартной детали при условии, что в первый раз извлечена деталь: а) стандартная; б) нестандартная.
Решение. Пусть события A и B – извлечение стандартной детали соответственно в первый и второй раз. Очевидно, что P(A) = 64 . Если вынутая деталь вновь возвращается в ящик, то
вероятность извлечения стандартной детали во второй раз |
P(B) = |
4 |
. |
Если вынутая деталь в |
||||||
6 |
||||||||||
|
|
|
|
|
|
|
|
|
||
ящик не возвращается, то вероятность извлечения стандартной детали во второй раз |
зави- |
|||||||||
сит от того, какая деталь была извлечена в первый раз – стандартная (событие A) или бракован- |
||||||||||
ная (событие ). В первом случае P (B) = 3 , во втором случае P |
|
(B) = |
4 |
, так как из оставшихся |
||||||
|
|
|||||||||
A |
5 |
|
A |
5 |
|
|
||||
|
|
|
|
|||||||
пяти деталей стандартных будет соответственно 3 или 4.
Пример 1.13. Производится два независимых выстрела в одну и ту же мишень. Вероятность попадания при первом выстреле 0,7, при втором – 0,8. Найти вероятность попадания в мишень при двух выстрелах.
11

0,7, |
Решение. Обозначим попадание при первом выстреле через A, при втором – В. |
|
0,8. |
Попадание в мишень предполагает хотя бы одно попадание: или только при |
|
|
|
|
первом выстреле, или только при втором, или и при первом, и при втором. Значит, в задаче требуется найти вероятность суммы двух совместных событий A и B:
|
0,8 |
0,7·0,8 |
. |
Так как события A и B независимы, то |
, поэтому |
||
0,7 |
0,94. |
Пример 1.14. Ремонтное ателье обслуживает пять клиентов. Вероятность вызова на обслуживание от каждого клиента равна 0,2. Какова вероятность, что в данный момент ателье занято обслуживанием клиентов?
|
Решение. Очевидно, что событие A={быть занятым обслуживанием клиентов} есть сум- |
|||
ма |
|
· · · · |
где |
быть занятым обслуживанием i-го клиента}, |
деляется0,2. |
|
{не быть занятым обслуживанием клиентов} опре- |
||
|
событий |
Противоположное…событие, |
||
|
как |
|
, значит, можно применить формулу (1.9): |
|
P( A) =1 − P( Ai )5 =1 − (1 − 0,2)5 = 0,918 .
Пример 1.15.. Сколько раз надо подбросить игральную кость, чтобы с вероятностью, меньшей 0.3, можно было ожидать, что ни на одной из выпавших граней не появится шесть очков?
Решение. Введём обозначение событий: A – ни на одной из выпавших граней не появится 6 очков; на выпавшей грани i-той кости ( i =1,2,...,n ) не появится 6 очков.
Вероятность того, что на любой выпавшей грани появится число очков, не равное шести,
равна P(Ai ) = 65 . События |
, ,…, |
независимы в совокупности, поэтому |
|||||||
По условию |
|
5 n |
· |
· …· |
· …· |
|
. |
||
|
|||||||||
|
|
< 0,3 . Следовательно, n ln(5 / 6) < ln 0,3 . Отсюда, учитывая, что ln(5 / 6) < 0 , |
|||||||
|
|
|
6 |
|
|
|
|
|
|
найдём, что n > |
|
ln 0,3 |
≈ 6,6 |
. Таким образом, число игральных костей n ≥ 7 . |
|||||
ln(5 / 6) |
|||||||||
|
|
|
|
|
|
||||
1.21.Отдел технического контроля проверяет изделия на стандартность. Вероятность того, что изделие стандартно, равна 0,9. найти вероятность того, что из двух проверенных изделий только одно стандартно. (0,18)
1.22.Слово АНАНАС разрезали на карточки, перевернули буквами вниз и перемешали. Карточки выбирают наугад по одной и выкладывают в ряд. Какова вероятность, что при этом получится слово АНАНАС? (1/60.)
1.23.На тепловой электростанции 15 сменных инженеров, из них 3 женщины. В смену занято 3 инженера. Найти вероятность, что в случайно выбранную смену мужчин окажется не менее 2. (0,9187.)
1.24.Для производственной практики на 30 студентов предоставлено 15 мест в Барнауле, 8
вБийске и 7 в Рубцовске. Какова вероятность, что два определённых студента попадут на практику в один город? (0,331.)
1.25.Доказать свойства условной вероятности:
1. |
0 |
1 |
; |
|
2. |
; |
|||
1 |
3.1;
12
4. |
еслиС |
, |
Ø |
С |
0 |
|
С |
; |
5. |
; |
|
||||||
|
, тоС |
|
|
|||||
6. |
если |
|
то |
1 |
. |
|
|
|
|
|
|
|
|
1.26.При изготовлении детали заготовка должна пройти 4 операции. Полагая появления брака на отдельных операциях событием независимым, найти вероятность изготовления стандартной детали, если вероятность брака на первой операции равна 0,02, на второй – 0,01, на третьей – 0,02, на четвёртой – 0,03. (0,92.)
1.27.Абонент забыл последнюю цифру номера и набрал её наугад. Определить вероятность того, что ему придется звонить не более чем в три места. Как изменится вероятность, если известна, что забытая цифра нечётная? (0,3. 0,6.)
1.28.Рабочий обслуживает 3 станка. Вероятность того, что первый станок в течение часа не потребует обслуживания, равна 0,9, для второго станка эта вероятность равна 0,8 и для третьего 0,85. Найти вероятности следующих событий: а) в течение некоторого часа ни один станок не потребует обслуживания; б) только один станок потребует внимания; в) хотя бы один станок не потребует обслуживания. (а) 0,612, б) 0,329, в) 0,997.)
1.29.Дана электрическая цепь. Вероятности отказа отдельных узлов за время T заданы таб-
лицей:
|
|
|
|
|
0,2 |
0,3 |
0,1 |
0,1 |
0,3 |
|
|
|
|
|
Схема выходит из строя, если цепь разомкнута. Определить вероятность безотказной работы за время T.
1.6 Формула полной вероятности. Формула Байеса
|
Теорема 1. Пусть событие A может произойти только с одним из несовместных событий |
||||
|
|
,при,…, |
образующих полную группу, |
т.е. |
… |
(гипотез) |
.,Тогда имеет место формула полной вероятности (ФПВ): |
||||
1 и |
|
Ø |
|
… |
(1.10) |
|
Доказательство. По условию теоремы событие |
, где собы- |
|||
тия |
, |
,…, |
несовместны. Тогда |
… |
. |
|
|
|
… |
… |
|
n
Краткая запись ФПВ: P( A) = ∑P(Bi )PBi ( A) .
i=1
Пример 1.16. Электролампы изготавливаются на трёх заводах. Первый завод изготавливает 45% общего количества электроламп, второй – 40%, третий – 15%. Продукция первого завода содержит 70% стандартных ламп, второго – 80%, третьего – 81%. В магазин поступает продукция всех трёх заводов. Какова вероятность, что купленная в магазине лампа окажется стандартной?
13
Решение. Введём обозначения: купленная лампа изготовлена на первом заводе, лампа со второго завода, лампа с третьего завода и, наконец, событие A – лампа ока-
залась стандартной.
Из условия задачи следует, что:
По |
|
0,45 |
0,40 |
0,15 |
|
|
|
0,70 |
0,80 |
|
0,81 |
|
|
|
, |
, |
, |
|
|
|
, |
, |
. |
||
|
формуле полной вероятности (1.10): |
|
|
0,15·0,81 0,7565. |
|
|
||||||
Теорема 2 (формула |
0,45·0,70 |
0,40·0,80 |
|
|
||||||||
вместных событий , |
Байеса). Пусть событие A может произойти только с одним из несо- |
|||||||||||
,…, , образующих полную группу. Тогда: |
|
|
|
|||||||||
или |
|
|
|
|
|
|
|
… |
|
|
|
|
|
|
|
|
|
|
|
|
связаны между собой и дают прямое и об- |
||||
Формула полной вероятности и формула Байеса, где |
1, . |
|
|
1.12 |
||||||||
ратное решения одной проблемы. Прямая задача прогнозирует появление события A по извест- |
||||||||||||
ным до опыта вероятностям осуществления каждой гипотезы |
, а обратная дает пе- |
|||||||||||
реоценку вероятностей гипотез |
|
после того, как событие, |
A,…произошло, |
. |
||||||||
Пример 1.17. Завод-изготовитель, ,…прибора, |
оценивает его надежность в 95%, а исследова- |
|||||||||||
тельская лаборатория определяет надежность 80%. Путем эксперимента, проведенного потребителем, требуется установить, какой характеристике следует отдать предпочтение.
Решение. A – событие, состоящее в том, что прибор выдержал испытание, |
– противо- |
|||||||||||
положное событие. Если |
|
|
|
– события, состоящие в том, что верны данные соответствен- |
||||||||
но завода и лаборатории, то и |
|
0,8, |
|
0,05, |
|
0,2, |
|
|
||||
Естественно положить, |
0,95, |
0,95 |
0,5. |
|
|
|
||||||
|
|
|
что |
|
|
Тогда |
|
|
|
|||
|
0,5·0,95 |
|
0,54; |
|
0,05 |
|
0,2; |
|||||
0,5·0,95 |
0,5·0,8 |
|
1,75 |
|
|
0,05 |
0,2 |
|
||||
0,8 |
0,46; |
|
|
|
|
0,2 |
|
0,8. |
||||
0,95 |
0,8 |
|
|
|
|
|
0,05 |
0,2 |
|
|||
Только одна из найденных вероятностей относительно большая, это 0,8. Следовательно, если прибор не выдержал испытание, можно отдать предпочтение оценке, данной лабораторией.
1.30. Игра «последний герой». Каждому игроку дано по 2 белых и 2 черных камня и предложено разложить по двум непрозрачным сосудам произвольным образом. Ведущий наугад выбирает сосуд и наугад выбирает из него шар. Если шар белый – игрок остается в игре, если черный – покидает игру. Как нужно разложить шары по двум сосудам, чтобы иметь наибольший шанс остаться в игре?
Указание. Шары можно, например, разложить одним из следующих способов:
14
Рассмотрите другие способы и найдите вероятность вынуть белый шар в каждом случае. Большая вероятность подскажет правильный вариант.
1.31.Литьё в болванках поступает из двух заготовительных цехов.: 70% из первого и 30% из второго. При этом продукция первого цеха имеет 10% брака, а второго – 20%. Найти вероятность того, что взятая наугад болванка без дефекта. (0,87.)
1.32.В трёх урнах находятся белые и черные шары: в первой урне 2 белых и 4 чёрных шара, во второй –3 белых и 5 чёрных, в третьей – 4 белых и 6 чёрных шаров. Из первой урны взяли наудачу 2 шара и переложили во вторую. После этого взяли 2 шара из второй урны и переложили в третью. Наконец, из третьей урны в первую переложили 2 шара. Найти вероятность того, что состав шаров во всех урнах не изменился. (173/495
1.33.Некто, заблудившись в лесу, вышел на поляну, откуда вело 5 дорог. Известно, что вероятности выхода из леса за час для различных дорог равны соответственно: 0,6; 0,3; 0,2; 0,1; 0,1. Чему равна вероятность, что заблудившийся пошел по первой дороге, если известно, что он вышел из леса через час? (6/13.)
при |
1.34. По линии связи передается кодированный с помощью букв A, B, C текст. |
|
||
0,3, |
0,2 |
вероятности передачи букв без искажения. Вероятности |
искажения |
|
|
|
|
0,5, |
|
передаче соответственно равны 0,01; 0,03; 0,02. Установлено, что сигнал из двух букв был принят без искажения. Чему равна вероятность того, что передается сигнал AB? (0,254)
2 Повторные независимые испытания
Некоторые испытания называются независимыми относительно события A, если вероятность наступления события A в каждом испытании не зависит от исходов других испытаний. Если независимые повторные испытания проводятся при одном и том же комплексе условий S, то вероятность в каждом испытании одна и та же. Описанная последовательность испытаний называется схемой Бернулли – по имени швейцарского математика XVII века Якоба Бернулли.
Такая схема описывает многие реальные ситуации: 1) проверяются n изделий, событие A –
появление события с браком, |
– вероятность того, что среди n изделий окажется k брако- |
|
ванных; 2) регистрируются n новорожденных, событие A – рождение девочки, |
– вероят- |
|
ность того, что среди n новорожденных k девочек; 3) имеется n инвестиционных проектов, событие A – прибыль в первый год работы проекта, – вероятность того, что из n только k проектов принесут прибыль в первый год работы. Тогда возникает задача – вычислить искомую вероятность .
2.1 Формула Бернулли
Теорема. Пусть комплекс условий S воспроизводится n раз, причём каждый раз событие A может наступить с одной и той же вероятностью p (0 1) независимо от результатов предыдущих опытов. Тогда вероятность того, что событие A произойдёт ровно k раз в n испытаниях, определяется по формуле Бернулли
где |
1 |
вероятность не появления в одном, |
испытании. |
(2.1) |
||||
|
Доказательство. Пусть |
|
соответственно появление и непоявление события A в |
|||||
единичном испытании, |
|
событие, состоящее в том, что в n независимых испытаниях собы- |
||||||
|
|
и |
… |
… |
… |
… . |
||
тие A появилось ровно k раз. Тогда |
||||||||
|
|
… |
|
… |
||||
|
появлений непоявлений |
|
|
непоявлений появлений |
||||
|
|
|
|
|
15 |
|
|
|
Всего получим |
слагаем ых ( |
сколькими способами можно расположить |
объектов |
||||
по местам без учета порядка) . Тогда |
|
|
|
|
|
||
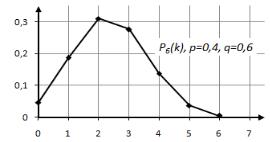
Чтоб ы нагляднее представить свойства ряда вероятностей |
…, |
…, |
, в |
||||
прямоугольной системе координат отмечают точки с координатами |
|
|
и соеди- |
||||
няют их ломаной (р исунок 2.1). |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рисунок 2.1
Число наступлений события называется наивероятнейшим, если вероятность наступления события данное число раз в этой серии испытаний наибольшая по сравнению с вероятностями
других исходов. На рисунке 2. 3 наивероятнейшее число |
. |
|
|||
Пусть |
n – число независимых испытаний, p – вероятность наступления события в отдель- |
||||
ном испытании. Тогда наивероятнейшее число наступлений события |
удовлетворяет нера- |
||||
венству |
|
|
|
|
|
|
|
|
|
, |
(2 .2) |
где |
. |
|
|
|
|
Так как разность |
|
, то всегда найдётся целое число , удовлетво- |
|||
ряющее написанному выше двойному неравенству. При этом, если |
целое число, то |
||||
наивероятнейших чи сел два: |
и |
. |
|
|
|
Прим ер 2.1. Вероятность изготовления на автоматическом станке стандартной детали равна 0,8. Найти наивер оятнейшее число появления бракованных деталей из 5 отобранных и веро-
ятность этого числа. |
|
|
|
|
Реш ение. Вер оятность изготовления бракованной детали |
. По формуле |
|||
(2.2): |
|
или |
. |
|
Единственное целое число, |
удовлетворяющее этому неравенству, |
, его вероятность |
||
находим п о формуле Бернулли |
|
|
|
|
P (1) = C1 0,21 0,84 = 0,4096 . |
|
|
|
|
5 |
5 |
|
|
|
Прим ер 2.2. Сколько раз надо подбросить игральную кость, чтобы наивероятнейшее число
выпадений двойки было равно 32? |
|
|
|
|
|
|
|
|
|
|
Реш ение. В данном случае |
|
|
, |
. Требуется найти число независимых испы- |
||||||
таний n. Величины p, q =1 − p, k0 , n |
|
|
связаны |
|
между собой соотношением (2.2): |
|||||
np − q ≤ k0 ≤ np + p , откуда |
1 |
|
|
5 |
|
1 |
|
1 |
|
|
n |
− |
≤ 32, n |
+ |
≥ 32. |
||||||
6 |
6 |
6 |
|
|||||||
|
|
|
6 |
|
||||||
Из первого неравенства n ≤197 , а из второго n ≥191 . Таким образом, необходимо провести от 191 до 197 подбрасываний игральной кости.
16

2.2 Формулы Лапласа. Формула Пуассона
При больших значениях n использование формулы Бернулли связано с трудоёмкими вы-
числениями. Пусть нам нужно вычислить |
50 : |
|
|
|
50 |
300! |
· |
· |
. |
50!250! |
Ясно, что это технически сложно. В подобных случаях используют формулу, являющуюся предельным случаем формулы Бернулли.
Локальная формула Лапласа. Если вероятность p появления события A постоянна в каждом испытании и отлична от 0 и 1, то вероятность того, что событие A наступит k раз в n независимых испытаниях, при достаточно большом числе n приближенно равна
P (k) ≈ |
1 |
ϕ (x) , |
(2.3) |
n npq
где ϕ (x) = |
1 |
e−x2 / 2 – функция Гаусса (рисунок 2.2), |
x = |
k −np |
. |
|
2π |
|
|
npq |
|
|
|
|
|
Рисунок 2.2 |
9 |
|
|
|
|
|
Чем больше n, тем точнее формула (2.3). При |
она даёт удовлетворительные для |
|||||||||
практики результаты. |
|
|
|
|
|
|
|
|
||
Значения функции Гаусса |
|
приведены в таблице II приложений. |
|
|
||||||
Свойства функции Гаусса: |
|
|
|
|
|
∞ |
0 |
|
||
1. |
– четная функция, т.е. |
|
. |
|
|
|
||||
2. функция |
монотонно убывает при x>0, причем при |
(практически |
||||||||
можно считать, что уже при |
|
|
). |
|
|
|
||||
Пример 2.3. Вероятность |
изготовления детали высшего сорта на данном станке равна 0,4. |
|||||||||
4 |
0 |
|
|
|
|
|
|
|||
Какова вероятность, что среди наудачу взятых 56 деталей половина окажется высшего сорта?
Решение. n большое, |
, поэтому применим локальную формулу Лапласа |
(2.3). Проведём необходимые |
вычисления: |
13,44 9 |
0,4, |
|
|
|
|
1 |
0,4 |
0,6, |
56, |
|
28, |
|
|
|
||||
56·0,4 |
22,4, |
|
22,4·0,6 |
13,44, |
|
|
|||||||||||
|
|
|
|
|
13,44 |
3,7, |
|
28 |
|
22,4 |
5,6, |
|
|
||||
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
√ |
|
|
|
5,6 |
1,51, |
1,51 |
0,1276, |
|
28 |
0,1276 |
|||
|
|
|
|
|
|
|
|
|
|||||||||
Следующая |
|
3,7 |
|
|
|
|
|
|
|
3,7 |
|||||||
|
|
|
|
|
|
|
|
формула Лапласа позволяет находить вероятность |
|||||||||
событие A в n независимых испытаниях наступит не менее |
и не более |
||||||||||||||||
0,034.
того, что
раз.
Интегральная формула Лапласа. Если вероятность p наступления события A в каждом испытании постоянна и отлична от 0 и 1, то вероятность того, что событие A в n независимых ис-
17
пытаниях наступит не менее |
и не более |
|
|
раз, при достаточно большом числе n приближен- |
|||||||||||||||||||||
но равна |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ф |
|
Ф |
, |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
x |
−t 2 |
/ 2 |
|
|
|
(2.4) |
|||||
|
|
|
|
|
|
|
Φ |
(x) = |
|
|
|
∫e |
|
|
|
dt – |
функция Лапласа, |
|
(2.5) |
||||||
|
|
|
|
|
|
|
|
2π |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
= |
k1 −np |
, |
|
x |
2 |
= |
k2 −np |
|
|
|
|
(2.6) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
1 |
|
npq |
|
|
|
|
npq |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
При |
|
|
формула (2.4) дает, как правило, удовлетворительную для практики погреш- |
||||||||||||||||||||||
ность |
вычисления вероятности. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ф |
|
|
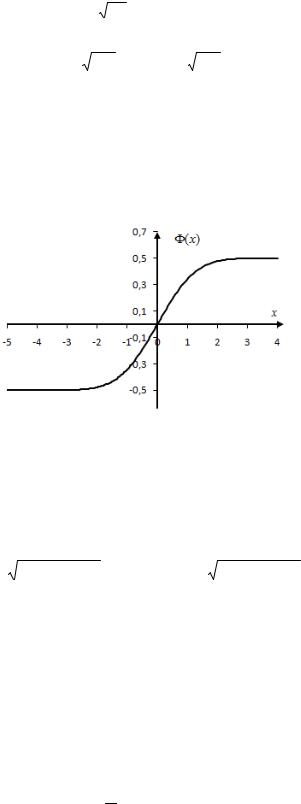
Значения функции |
|
можно найти в таблице III |
приложений. График |
изображён |
|||||||||||||||||||||
на рисунке 2.3. |
Перечислим свойства функции Лапласа. |
|
|
|
|
|
|||||||||||||||||||
Ф |
|
Ф |
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ Ф |
0,5 |
|
|
||||||
1.Функция |
нечетная, т. е. |
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
||||||||||
тать, что уже |
|
|
|
|
). |
|
|
|
|
при |
|
|
|
(практически можно счи- |
|||||||||||
2.Функция |
Ф |
монотонно |
возрастает, |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
Ф |
|
|
Ф |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
при |
5 Ф |
0,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Рисунок 2.3
Пример 2.4. В некоторой местности из каждых 100 семей 80 имеют холодильник. Какова вероятность, что от 300 до 360 семей включительно из 400 обследованных имеют холодильники?
Решение. Применим интегральную формулу Лапласа ( |
64 9 |
. Вначале опреде- |
лим по формулам (2.6) |
|
x = |
300 − 400 0,8 |
= −2,50, |
x |
2 |
= |
360 − 400 0,8 |
=5,0 . |
||
|
|
||||||||
1 |
400 |
0,8 0,2 |
|
|
400 |
0,8 0,2 |
|
||
|
|
|
|
|
|||||
Далее по формуле (2.4), учитывая свойства функции Φ(x), получим:
P400 (300 ≤ k ≤360) ≈ Φ(5,0) − Φ(−2,50) ≈ ≈ Φ(5,0) + Φ(2,50) ≈ 0,5 + 0,4938 ≈ 0,9938 . (Из таблицы III приложений: Φ(2,50) ≈ 0,4938, Φ(5,0) ≈ 0,5 ).
Рассмотрим следствие интегральной формулы Лапласа.
Следствие. Если вероятность p наступления события A в каждом испытании постоянна и отлична от 0 и 1, то при достаточно большом числе независимых испытаний вероятность следующих событий определяются по формулам:
а) относительная частота mn события A заключена в пределах от α до β:
Φ |
Φ , |
(2.7) |
18

где |
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
б) относительная частота m |
события A отличается от его вероятности |
не более, чем на |
|||||||||||||||||||
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
величину ∆ 0 (по абсолютной величине): |
|
∆ |
√ |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
∆ |
Φ |
|
|
. |
|
|
2.8 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
При |
|
и |
|
|
|
|
|
|
|
|
формулы Лапласа дают удовлетворительную |
||||||||||
для практики |
погрешность вычисления вероятности. Если n одного порядка с 1/n при больших |
||||||||||||||||||||
9 1/ |
1 |
/ |
1 |
|
|
Пуассона |
|
||||||||||||||
n, или |
0,1, более точный результат дает формула |
|
|
|
λk e−λ |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
Pn (k) ≈ P(k) = |
|
|
k! |
, |
(2.9) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где λ = np .
Пример 2.5. На факультете 730 студентов. Какова вероятность того, что 1 сентября является днём рождения одновременно трёх студентов?
Решение. Вероятность того, что день рождения для отдельного студента 1 сентября, равна p=1/365<0,1. Применяем формулу Пуассона (2.7). В нашем случае n=730, p=1/365, k=3, поэтому
λ = np = 730 3651 = 2, P730 (3) ≈ P(3) = λ3 3e! −λ = 0,18045 .
Таким образом, в среднем в 18 случаях из ста на 1 сентября приходится день рождения трёх студентов факультета.
Пример 2.6. Вероятность появления события в каждом из 400 независимых испытаний
равна 0,8. Найти такое число |
|
|
, чтобы с вероятностью 0,9876 абсолютная величина откло- |
|||||||||||
нения относительной частоты |
появления события от его вероятности 0,8 не превысила |
|||||||||||||
|
0 |
|
0,8, |
0,2. |
Подставим в формулу (2.8): . |
|||||||||
Решение. По условию |
|
400, |
||||||||||||
|
|
|
|
|
|
|
||||||||
2Ф |
|
|
0,9876 |
|
|
Ф 50 |
0,4938. |
|
|
|
|
|
||
, |
· , |
|
|
|
50 |
2,5 |
|
0,05. |
||||||
|
|
|
|
|
|
|
|
|||||||
По таблице значений функции Лапласа находим |
||||||||||||||
|
|
|
||||||||||||
2.1.Доля изделий высшего сорта на данном предприятии составляет 87%. Сколько изделий высшего сорта следует ожидать в случайно отобранной партии из 400 изделий? (348.)
2.2.Сколько нужно взять деталей, чтобы наивероятнейшее число годных деталей было равно 50, если вероятность того, что наудачу взятая деталь будет бракованной, равна 0,1? (55
или 56.)
2.3.Из большой партии изделий берут на пробу 10 штук. Известно, что доля нестандартных изделий во всей партии составляет 10%. Какова вероятность, что среди отобранных стандартных изделий будет 8? (0,194.)
2.4.Среди изделий некоторого цеха брак встречается с вероятностью 0,015. Найти вероятность, что среди 200 изделий бракованных окажется: а) 5; б) не более 5. (а) 0,1008; б) 0,916.)
2.5.На каждую 1000 букв русского в среднем приходится 110 букв «о». Какова вероятность, что в тексте из 4000 букв буква «о» встретится от 400 до 500 раз? (0,97795)
19
2.6. Автоматическая штамповка клемм для предохранителей даёт 10% отклонений от заданного стандарта. Сколько стандартных клемм следует ожидать с вероятностью 0,0587 среди
400клемм? (360±3.)
2.7.Отдел технического контроля проверяет на стандартность 900 деталей. Вероятность того, что деталь стандартна, равна 0,9. Найти с вероятностью 0,9544 границы, в которых будут
заключено число k стандартных деталей среди проверенных. (792 |
828.) |
2.8.На тарелке лежат три апельсина, пять яблок и четыре груши. Дети съели 4 фрукта. Какова вероятность, что они съели: а) апельсин, два яблока и грушу; б) 4 яблока; в) по крайней мере, два яблока? (Ответ: а) 8/33; б) 1/99; в) 19/33.)
2.9.В ящике находятся катушки с нитками четырех цветов: белого –50%, красного – 20%, зеленого – 20%, синего –10%. Какова вероятность, что взятая наудачу катушка окажется с нитями синего или зеленого цвета? (Ответ: 0,3)
2.10.Отдел технического контроля обнаружил пять бракованных книг в партии из случайно отобранных 100 книг. Найти относительную частоту появления бракованных книг. (Ответ: w( A) = 0,05 .)
2.11.Пятитомное собрание сочинений расположено на полке в случайном порядке. Какова вероятность того, что книги стоят слева направо в порядке нумерации (от 1 до 5)? (Ответ: 1/120.)
2.12.Из ящика, содержащего 5 пар обуви, из которых 3 пары мужской, а две пары женской обуви, перекладывают наудачу две пары в другой ящик, содержащий одинаковое количество пар женской и мужской обуви. Какова вероятность, что во втором ящике после этого окажется одинаковое количество пар мужской и женской обуви? (Ответ: 0,6.)
2.13.Страховая компания разделяет застрахованных клиентов по классам риска: I класс – малый риск, II класс – средний, III класс – большой риск. Среди застрахованных клиентов 50% первого класса риска, 30% – второго и 20№ – третьего. Вероятность необходимости выплачивать страховое вознаграждение для первого класса равна 0,01, второго – 0,03, третьего – 0,08. Найти вероятность того, что: а) застрахованный получит денежное вознаграждение за период страхования; б) получивший денежное вознаграждение застрахованный относится к группе ма-
лого риска. (Ответ: а) 0,03; б) 0, 167.)
2.14.В группе из 20 студентов, пришедших на экзамен. 6 подготовлены отлично, 8 – хорошо, 4 – посредственно и 2 – плохо. В экзаменационных билетах имеется 40 вопросов. Отлично подготовленный студент может ответить на все 40 вопросов, хорошо подготовленный – на 32 , посредственно – на 20, плохо – на 10. Вызванный наугад студент ответил на три произвольно заданных вопроса. Найти вероятность того, что студент подготовлен: а) отлично; б) плохо. (Ответ: а) ≈ 0,579 ; б) ≈ 0,002 .)
Примерный вариант контрольной работы
1.Общество из 15 человек садится за круглый стол. С какой вероятностью два определённых лица окажутся рядом? ( P =1/ 7 .)
2.Из 18 стрелков шесть попадают в мишень с вероятностью 0,8, восемь – с вероятностью 0,7, а остальные – с вероятностью 0,6. Один из стрелков сделал выстрел, но в мишень не попал.
Ккакой из перечисленных групп вероятнее всего принадлежит этот стрелок?
( P(1) =12 / 52 , P(2) = 24 / 52, P(3) =16 / 52 , т.е. ко второй.)
3.Семён на охоте стреляет по зайцам. Вероятность попадания при каждом выстреле равна 0,2. Найти вероятность того, что пятым выстрелом он убьёт третьего зайца. ( P = 0,03072 .)
4.Число коротких волокон в партии хлопка составляет 25%. Какова вероятность, что в пучке из 432 волокон коротких будет не менее 100 и не более 130? ( P = 0,5588 .)
5.Доля изделий высшего сорта на данном предприятии составляет 31%. Сколько изделий надо взять, чтобы наивероятнейшее число изделий высшего сорта было равно 23? (От 74 до 76 изделий.)
20
