Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Алтайский государственный технический университет им. И.И.Ползунова

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Gladysheva-tv (1)

.pdf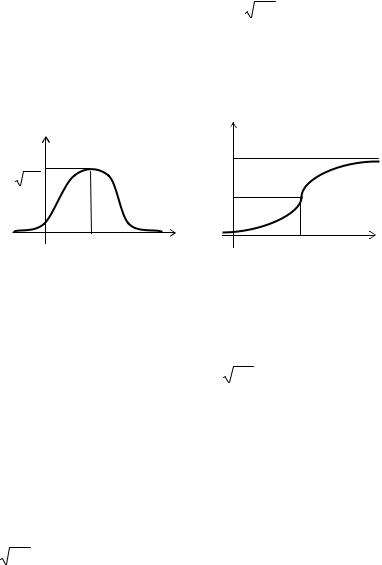

Скачиваний:

Добавлен:

14.02.2015

Размер:

900.71 Кб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 107 8 9 10 > Следующая >>>

		1	е−	(х−а)2
f (x) =				2σ 2	,	(3.17)
	σ	2π

где

√

Кривую нормального закона распределения называют нормальной кривой или кривой Гаусса. Графики плотности и функции распределения нормального закона с параметрами , приведены на рисунке 3.5.

f ( x)

F ( x)

2π

0,5

a − 3σ

a + 3σ x

Рисунок 3.6

Нормальное распределение с параметрами

называется стандартным нор-

функцией Гаусса

мальным распределением. Его плотность задается

0 x2

е−

ϕ(x) =

2 .

2π

Свойства нормального распределения

;

1.Вероятность

попадания нормальной случайной величины в интервал

равна

P(α < X < β) = Φ

β − a

− Φ

α − a ,

(3.18)

∫x e−

где Φ(x) =

2 dt − функция Лапласа, ее значения приведены в таблице III прило-

2π

, рас-

жений. Так как Φ(−x) = −Φ(x) = −0,5 , то функция распределения случайной величины

пределённой по нормальному закону, определяется формулой:

F(x) =	1	x − a
		+ Φ		.	(3.19)
	2		σ

2. Вероятность того, что отклонение нормальной случайной величины от своего математи-

	величину	(по абсолютной величине), равна
ческого ожидания не превысит	P(	∆X −0a	≤	)= 2 Φ		(3.20)
	P(	∆X −0a	≤	)= 2 Φ		(3.20)
					σ
					σ

Найдем вероятности отклонения нормальной случайной величины от математического

ожидания на величину	∆ ;2 ;3P(.	X − a ≤σ )= 2 Φ(1) = 0 , 6827;
ожидания на величину		Значения функции Лапласа находим в приложении.

	P(	X −a		≤ 2σ )= 2Φ( 2) = 0,9545;	(3.21)
	P(	X −a		≤ 2σ )= 2Φ( 2) = 0,9545;
	P (	X − a	≤3σ )= 2 Φ( 3) = 0 , 9973.

Отсюда вытекает «Правило трех сигм»:

С вероятностью, практически равной единице, значения нормальной случайной величины

попадают в интервал

3 ;

3 .

Пример 3.16. Производится измерение без систематических ошибок диаметра вала. Случайная ошибка измерения X подчиняется нормальному закону распределения со средним квадратическим отклонением 20мм. Найти: а) вероятность того, что измерение будет произведено с ошибкой, по абсолютной величине не превосходящей 35 мм; б) интервал, в который попадет сл.в. X с вероятностью 0,6827.

Решение.

Ошибка измерения

это случайная величина,

20.

Так как по условию

систематическая ошибка отсутствует, то

=0.2 Φ(1,75) = 0,9198.

а) По формуле 3.20 P(

< 35) = 2 Φ

б)

=1, = 20 X (−20;20).

) = 2 Φ

= 0,6827,

= 0,34135,

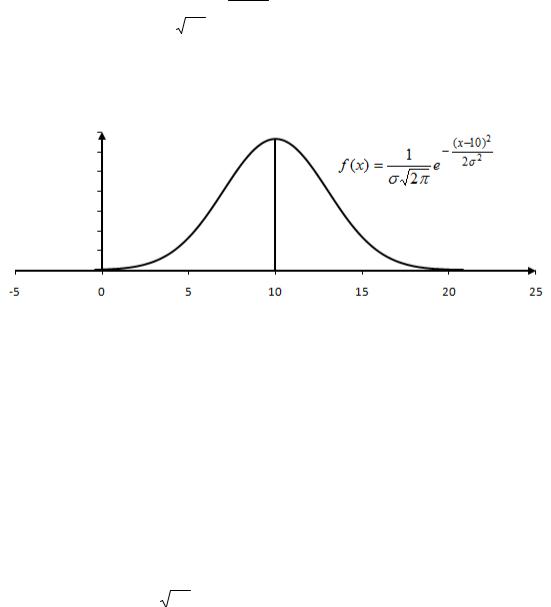
Пример 3.17. Случайная величина

распределена нормально с математическим ожидани-

ем

10. Вероятность попадания

в интервал (10;20) равна 0,3. Найти вероятность попада-

ния в интервал (0;10). f (x) =		1	е
	σ	2π

− (х−10)2 2σ 2

Решение. Так как нормальная кривая симметрична относительно кривой		то
площади, ограниченные сверху нормальной кривой и снизу – интервалами (0;10) и	(10;20), рав-
	10,

ны между собой.

Поскольку эти площади численно равны вероятностям попадания в соответствующий интервал, то

Пример 3.18. Полагая,	0	10	10	20	0,3.2
	что рост мужчин определённой возрастной группы есть нормально

распределённая случайная величина X с параметрами a =173, σ = 36 , найти:

1.а) выражение плотности вероятности и функции распределения случайной величины X ; б) долю костюмов 4-го роста (176 – 182 см ), которую нужно предусмотреть в общем объёме производства для данной возрастной группы.

2.квантиль x0,7 и объяснить смысл полученного значения.

3.Сформулировать правило «трёх сигм» для случайной величины X .

Решение. 1. а) По формулам (3.17) и (3.19) запишем плотность распределения и функцию распределения:

f (x) =	1	e−(x−173)	2	/ 72 ,	x −173
					F(x) = 0,5 + Φ		.
	6 2π				F(x) = 0,5 + Φ	6	.
	6 2π					6
				62

б) Доля костюмов 4-го сорта в общем объёме производства определяется по формуле (3.16) как вероятность попадания сл.в. X в заданный интервал:

P(176 ≤ X ≤182) = Φ(t2 ) − Φ(t1 ) = Φ(1, 50) − Φ( 0 , 50) = 0,4332 − 0,1915 = 0,2417.

Здесь t =	176 −173	= 0 , 5,	t	2	=	182 −173	=1, 5 .

1	6				6

Таким образом, для данной возрастной группы в общем объёме производства нужно предусмотреть примерно 24% костюмов.


		1	x	0,7	−173			x	0,7	−173
	F(x0,7 ) =	1		0,7					0,7		= Φ(t) = 0,2 .
2.			+Φ				= 0,7, Φ
2.		2	+Φ		6		= 0,7, Φ			6
		2			6					6
По таблице III приложений найдём t = 0 , 52 и
						x0,7		= 6t +173 = 6 0,52 +173 ≈176 (см) .

Это означает, что 70% мужчин данной возрастной группы имеют рост до 176 см.

3.Практически достоверно, что рост мужчин данной возрастной группы заключён в гра-

ницах от a −3σ =173 −3 6 =155 до a +3σ =173 + 3 6 =191, т.е. 155см ≤ X ≤191см .

Пример 3.19. Значения случайной величины X с вероятностью 0,9973 попадают в интервал (−5;7) . Найдите математическое ожидание и дисперсию этой случайной величины.

Решение. Таким свойством обладает нормально распределённая случайная величина,

поэтому MX = −52+ 7 =1, σ = 7 −6(−5) = 2 , DX = 22 = 4.

В силу особенностей нормального закона распределения, отмеченных в начале параграфа, он занимает центральное место в теории и практике вероятностно-статистических методов.

3.17. Автомат штампует детали. Контролируется длина детали X, которая распределена нормально с математическим ожиданием (проектная длина), равной 50 мм. Фактическая длина изготовленных деталей не менее 32 мм и не более 68 мм. Деталь считается годной, если отклонение её длины от проектной не превышает σ. Сколько процентов годных деталей штампует автомат?

3.18. Случайная величина X распределена нормально с параметрами	2,	0,1.	Найти
интервал, в котором с вероятностью 0,9973 будут заключены значения сл.в. X.

3.19. Значения случайной величины X с вероятностью 0,9545 попадают в интервал (2;10). Найдите математическое ожидание и дисперсию этой случайной величины

3.11 Показательный закон распределения. Функция надёжности

Определение. Показательным (экспоненциальным)				называют распределение вероят-
ностей непрерывной случайной величиныf (t),			которое описывается плотностью
ностей непрерывной случайной величиныf (t),			= 0 при t < 0,		(3.22)
			λe−λt при t ≥ 0.

Здесь параметр
Функция	распределения показательного закона
Функция		0.

		t	t
	F(t) = ∫ f (t)dt = ∫λe−λt dt =1 −e−λt .
		−∞	0
Тогда в окончательном виде
			0 при	t < 0,		(3.23)
			F(t) =	при t ≥ 0.		(3.23)
			1 −e−λt	при t ≥ 0.
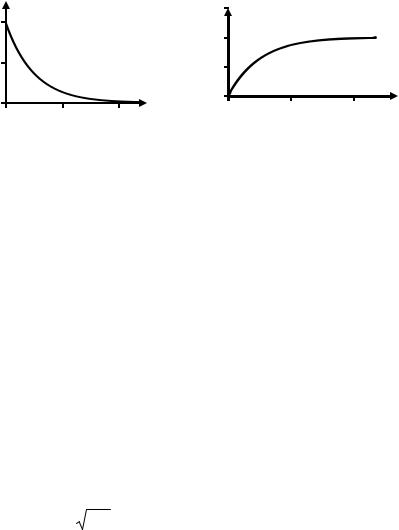
					2 изображены на рисунке 3.7.
Графики плотности и функции−2t		распределения при λ
Графики плотности и функции−2t			1,5
2	f (t) = 2e			F(t) =1−e−2t
			1
1			0,5
			0,5
0		t	0			2 t
0			0		1
0	1		0		1
0	1	2

Рисунок 3.7.

Вероятность попадания показательно распределенной случайной величины в интервал

,определяется формулой

P(α <T < β) = F(β) − F(α) =1−e−λβ −(1−e−λa ) = e−λ a −e−λβ .

Определим числовые характеристики показательного закона распределения – математическое ожидание и дисперсию.

+∞

M T = ∫t λe−λ t d x =

−t e−λt −

−λ t

DT = M T 2 − (M T )2

+∞

M T 2 = ∫t 2λe−λ t dt = − ∫t 2d e−λ t = −t 2 e−λ t

∫e−λ t 2t dt =

+∞

= 2

∫t λe−λ t dt =

DT =

−

. σ = DT =1/ λ .

λ 2

λ2

λ 2

Итак,

M T =1/ λ, DT =1/ λ2 , σ =1/ λ .

Показательный закон распределения играет большую роль в теории массового обслуживания и теории надежности.

Показательный закон распределения (и только он) обладает важным свойством, которое мы рассмотрим в примере 3.23.

Пример 3.20. Доказать, что если промежуток времени T, распределенный по показательному закону, уже длился некоторое время τ, то это никак не влияет на закон распределения оставшейся части T1= T – τ промежутка, т.е. закон распределения T1 остаётся таким же, как и всего промежутка T.

Решение.			Пусть функция распределения промежутка T определяется формулой (3.23),
бытиет.е.	1		функция распределения оставшейся части T = T – τ при условии, что со-
бытиет.е.	1	произошло, а		, есть	условная вероятность		события		1		относительно события
, т.е.					. Так как		,
то полагая				,	,	получим				.
то полагая						получим

Произведение событий						равносильно событию					,	вероятность
которого											1	.
Вероятность				1		1		. Тогда			1	.
деления											искомая функция распре-
деления
				1		1		1			.

Пример 3.21. Время расформирования состава через горку – случайная величина, подчиненная показательному закону. Пусть 5 – среднее число поездов, которые горка может расформировать за 1 час. Определить вероятность того, что время расформирования состава: 1) меньше 30 мин; 2) больше 6 мин, но меньше 24 мин.

Решение. 1 ) Вероятность	того,	что	время	расформирования состава займёт менее
30 мин = 0,5 ч, есть	0,5	1	· ,	1 0,082 0,918.
0,5

1) Вероятность того, что время расформирования состава займет от 6 мин = 0,1 ч до

24 мин = 0,4 ч:

0,1

0,4

· ,

0,6065 0,1353 0,4712.

Функция надёжности

Элементом называют некоторое устройство, независимо от того, «простое» оно или «сложное». Пусть элемент начинает работать в момент времени t0 = 0 , а в момент t происходит

отказ. Обозначим через T непрерывную случайную величину – длительность времени безотказной работы элемента, а через – интенсивность отказов (среднее число отказов в единицу времени).

Часто длительность времени безотказной работы элемента имеет показательное распределение с функцией распределения

F (t) = P(T < t) =1 − e−λ t (λ > 0, t > 0) ,

которая определяет вероятность отказа элемента за время длительностью t.

Функцией надёжности называют функцию, определяющую вероятность безотказной работы элемента за время длительностью t:

R (t ) = e−λ t .

Пример 3.22. Длительность времени безотказной работы элемента имеет показательное распределение F (t) =1 − e−0,02 t (t > 0) . Найти вероятность того, что за время длительностью

25ч : а) элемент откажет; б) элемент не откажет.

Решение. а) Так как функция распределения F (t) =1 − e−0,02t определяет вероятность отказа элемента за время длительностью , то вероятность отказа:

F (25) =1 − e−0,02 25 =1 − e−0,5 =1 − 0,606 = 0,394 ;

б) события «элемент откажет» и «элемент не откажет» – противоположные, поэтому вероятность того, что элемент не откажет

P =1 − 0,394 = 0,606 .

Этот же результат можно получить, пользуясь функцией надёжности R (t ) = e−λ t , определяющей вероятность безотказной работы элемента за время длительностью t:

R (25) = e−0,02 25 = e−0,5 = 0,606 .

3.12 Другие виды распределения

Пример 3.23. Случайная величина X подчинена закону Симпсона («закону равнобедренного треугольника») на участке от –a до a.

Найти: 1) плотность распределения; 2) числовые характеристики случайной величины; 3) вероятность попадания в интервал – /2; .

Решение. 1) Площадь под графиком плотности равна 1

1	·2 ·	1		1
2	·2 ·	1

Уравнения прямых, задающих плотность распределения:

0	1	0	0	при		;0 ,

0	1	0	0		при	0;

В остальных точках числовой прямой плотность распределения равна нулю.

2) В силу симметричности плотности распределения математическое ожидание равно нулю: MX=0. Найдём дисперсию:

	4		3	0	4	3		0			4		3	4		3	6	.
3		2			1				2		1	/
3		2			1			1	2		1	/		7
							1	1		·			/2	7	.
							1			·	2		/2	8	.

Упражнение. Случайная величина X подчинена закону Симпсона на участке от –a до a. Найти функцию распределения.

3.13 Функции от непрерывных случайных величин

Пусть задана плотность fX (x) случайной величины X и монотонная дифференцируемая

функция	. Тогда плотность распределения случайной величины			равна
		dϕ−1( y)
	fY ( y) = f (ϕ−1( y))	dϕ−1( y)	.
	fY ( y) = f (ϕ−1( y))	d y	.
		d y
Здесь ϕ−1( y)	– функция, обратная функции	.

Пример 3.24. Случайная величина X равномерно распределена на отрезке [0,2]. Найти

плотность случайной величины

√

Решение. Из условия задачи следует, что плотность случайной величины X имеет вид:

				0,			x [0, 2],
					1
			f X (x) =		1	,	x [0, 2].
					2	,	x [0, 2].
					2
		к
Найдём функцию, обратную		к	√	1 и её производную:
Найдём функцию, обратную		=	√	1 и её производную:
1,	2
1,	2

Функция обратную функцию

Следовательно,

fY ( y) =

Значит,

√1 – монотонная и дифференцируемая на отрезке [0,2]. Она имеет

	1, производная которой			dϕ−1( y)		= 2 y .
	1, производная которой			d y		= 2 y .
	dϕ−1( y)						2	−1 [0, 2],
							2
f (ϕ−1( y))		= f	(ϕ−1( y)) 2 \| y \|= 2 \| y \| 0, y
f (ϕ−1( y))		= f	(ϕ−1( y)) 2 \| y \|= 2 \| y \| 0, y
X	d y		X		1	, y2		−1 [0, 2].
X			X

					2
					2

	y [−	3,−1],
fY ( y) = 0,	y [−	3,−1],
− y,	y [−	3,−1].

3.14 Понятие о законе больших чисел и предельных теоремах

Закон больших чисел. Под законом больших чисел (ЗБЧ) в широком смысле понимается общий принцип, согласно которому по формулировке академика А.Н.Колмогорова, совокупное действие большого числа случайных факторов приводит (при некоторых весьма общих условиях) к результату, почти не зависящему от случая. Другими словами, при большом числе случайных величин их средний результат перестаёт быть случайным и может быть предсказан с большой степенью определённости.

Под ЗБЧ в узком смысле понимается ряд математических теорем, в каждой из которых для тех или иных условий устанавливается факт приближения средних характеристик большого числа испытаний к некоторым определённым постоянным. Исторически первой формулировкой ЗБЧ была теорема Бернулли.

Теорема Бернулли. Относительная частота события в n повторных независимых испытаниях, в каждом из которых оно может появиться с одной и той же вероятностью р, при неограниченном увеличении числа n сходится по вероятности к вероятности р этого события в отдельном испытании:

		m	− p

lim	P			≤ ε =1.	(11.33)

n→∞		n

Смысл теоремы Бернулли состоит в том, что при большом числе n повторных независимых испытаний практически достоверно, что относительная частота (или статистическая вероятность) события m / n – величина случайная, как угодно мало отличается от неслучайной величины р – вероятности события, т.е. перестаёт быть случайной. Поэтому теорема Бернулли даёт теоретическое обоснование замены неизвестной вероятности события его относительной частотой, или статистической вероятностью, полученной в n повторных независимых испытаний, проводимых при одном и том же комплексе условий.

Теорема Бернулли связывает формальное аксиоматическое определение вероятности с эмпирическим (опытным) законом постоянства относительной частоты, тем самым она даёт возможность обосновать широкое применение на практике вероятностных методов исследования.

Наиболее важной формой закона больших чисел является теорема Чебышева, следствием которой является теорема Бернулли.

Теорема Чебышева. Если независимые случайные величины X1, X 2 ,..., X n имеют одинако-

вое математическое ожидание, равное а, а их дисперсии ограничены одной и той же константой, то при неограниченном возрастании числа n средняя арифметическая случайных величин сходится по вероятности к математическому ожиданию а случайных величин:

	1	n

		∑X i − a
lim P			< ε	=1.	(11.34)

n→∞	n i=1

Центральная предельная теорема. Очень часто значение, которое принимает исследуемая случайная величина Y, является результатом суммарного воздействия ряда случайных факторов X1, X 2 ,..., X n . Если эти факторы слабо зависят друг от друга и ни один из них не является

доминирующим, то их сумма имеет распределение, близкое к нормальному. Такая ситуация наиболее характерна для процессов измерения. Дело в том, что результат измерения складывается под влиянием многочисленных независимых причин, причём влияние каждой из них на суммарный результат незначительно. Например, на величину температуры в конкретном месте в комнаты оказывает влияние близость отопительных приборов, наличие и расположение в комнате людей, потоки воздуха, влажность, температура воздуха на улице, наличие источников света и их мощность, расположение окон, дверей и т.д.

Вопросы для повторения

1.Что называется случайной величиной? Приведите примеры дискретных и непрерывных случайных величин.

2.Что такое функция распределения F(x) случайной величины X?

3.Перечислите свойства функции распределения.

4.Ряд распределения и функция распределения дискретной случайной величины.

5.Задаёт ли данная таблица закон распределения некоторой случайной величины? Обоснуёте свой ответ.

	–2	0	1
	0,2	0,05	0,3

4	6	8
0,1	0,05	0,2

6.	Дайте определение математического ожидания		дискретной случайной величины и
перечислите его свойства.
7.	Что такое дисперсия	случайной величины? Перечислите свойства дисперсии. Что та-
кое среднее квадратичное отклонение?
		68

8.Про какую величину говорят, что она имеет гипергеометрическое распределение?

9.Дайте определение биномиального закона распределения. Как вычисляются его числовые характеристики?

10.Какая случайная величина называется непрерывной?

11.	Перечислите свойства плотности	распределения вероятностей.
12.	Запишите формулы для вычисления математического ожидания		и дисперсии

непрерывной случайной величины , заданной на отрезке , .

13. В каких ситуациях применяется равномерный закон распределения? Назовите его числовые характеристики.

14. Дайте определение нормального закона распределения с параметрами a и . Нарисуйте

график плотности нормального распределения с параметрами

15.В чём заключается «правило трёх сигм»?

16.Запишите плотность и функцию распределения показательного закона распределения. Какое его отличительное свойство? Где он применяется?

17.Запишите числовые характеристики показательного закона с параметром λ=3.

18.Запишите плотность, функцию распределения, математическое ожидание и дисперсию закона Симпсона на отрезке [-5;5].

Примерный вариант контрольной работы по теме «Случайные величины»

1.В магазине имеется 20 телевизоров, из них 4 имеют дефекты. Необходимо: 1) составить закон распределения числа телевизоров с дефектами среди трех выбранных; 2) найти MX ; 3) определить вероятность того, что среди выбранных телевизоров не более двух с дефектом.

2.Известна функция распределения непрерывной случайной величины X :

0,		если х <1,
	А(х2 −1), если		1 ≤ x ≤ 3,
F (x) =
		если x > 3.
1,

Найти: 1)		неизвестный	параметр A ; 2) плотность распределения f (x) ; 3) M X , D X ; 4)

P(0,5 ≤ X < 2,3) ; 5) моду Mo(X ) и медиану Me ( X ) ; 6) построить графики f (x), F (x) .

3. Цена деления шкалы измерительного прибора равна 0,2. Показания прибора округляют до ближайшего целого деления. Полагая, что при отсчете ошибка измерения распределена по равномерному закону, найти: 1) математическое ожидание, дисперсию и среднее квадратичное отклонение этой случайной величины; 2) вероятность того, что ошибка округления: а) менее 0,04 ; б) более 0,05 .

(Ответ: 1: MX = 0,1; DX =1/ 300; σ = 0,0577; 2: а) 0,4; б) 0,5.)

4.Поезда данного маршрута городского трамвая идут с интервалом 7 минут. Пассажир подходит к трамвайной остановке в некоторый момент времени. Какова вероятность появления пассажира не ранее чем через две минуты после ухода предыдущего поезда, но не позднее, чем за три минуты до отхода следующего поезда? Время ожидания распределено по равномерному закону. (Ответ: 2/7.)

5.Цена некой ценной бумаги нормально распределена. В течение последнего года 30% рабочих дней она была ниже 72 ден.ед., а 50% – выше 78 ден.ед. Найти: 1) математическое ожидание и среднее квадратичное отклонение цены ценной бумаги; 2) вероятность того, что в день покупки цена будет за-

ключена в пределах от 63 до 90 ден.ед.(по абсолютной величине). (Ответ: a = 78; σ =11,4; P(63 < X < 9) = 0,76. )

Индивидуальные задания по теме «Случайные величины»

Вариант – 1

6. Вероятность поражения вирусным заболеванием куста земляники равна 0,2. Составить закон распределения случайной величины X – числа кустов земляники, зараженных вирусом, из трех посаженных кустов. Найти: 1) функцию распределения F(x) и построить ее график; 2) MX, DX и σ.

7. В чулане находится пять пар ботинок. Случайно выбирают 4 ботинка. Восстановить закон распределения случайной величины X – числа полученных пар ботинок среди четырех отобранных. Найти MX и DX.

8. Случайной величины X принимает два значения: x1 = 2 и x2. Найти функцию распределения

F(x), если MX = 3,4 и DX = 0,84.

9. Найти закон распределения случайной величины X-Y.

Проверить, что M(X-Y)=MX-MY, D(X-Y)=DX+DY.

	xi	-1	0	1		yi	0		2
	pi	0,2	0,3	0,5		qi	0,4		0,6
10. Известна функция распределения непрерывной случайной величины X:
			0,	если	х < 0,
			F(x) = А(1 −cos x), если 0 ≤ x ≤ π,
				если	x > π.
			1,	если	x > π.
Найти: 1) неизвестный параметр A; 2) плотность распределения f(x); 3) P π									≤ X <	3π	. По-
								2		2

строить графики f(x) и F(x).

11. Плотность распределения непрерывной случайной величины задается формулой:

0,		если	х <1
	А(х3 − x), если 1 ≤ x ≤ 2,
f (x) =
		если	x > 2.
0,

Найти: 1) неизвестный параметр A; 2) функцию распределения F(x); 3) MX, DX, σ. Построить график функции f(x).

12.Цена деления шкалы измерительного прибора равна 0,2. Показания прибора округляют до ближайшего целого деления. Полагая, что при отсчете ошибка измерения распределена по равномерному закону, найти: 1) математическое ожидание, дисперсию и среднее квадратическое отклонение этой случайной величины; 2) вероятность того, что ошибка округления: 1) менее 0,04; 2) более 0,05.

13.Распределение веса консервных банок, выпускаемых заводом, подчиняется нормальному закону распределения со средним весом 250 г и средним квадратическим отклонением, равным 5 г. Определить вероятность того, что отклонение веса банок от среднего веса по абсолютной величине не превысит 8 г.

<<< < Предыдущая 1 2 3 4 5 67 / 107 8 9 10 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
14.02.2015463.05 Кб108filosofiya_voprosy_s_otvetami.pdf
#
14.02.2015224.77 Кб6Fizicheskaya-kultura-123456-Dlya-vseh-B.doc
#
14.02.20152.12 Mб600FIZIKA-chast-3-2009.docx
#
17.09.20194.03 Mб18FIZIKA-chast-3-2009_-_kopia.doc
#
14.02.20152.21 Mб9FNP.doc
#
14.02.2015900.71 Кб85Gladysheva-tv (1).pdf
#
13.11.2019982.53 Кб29Glava_1.doc
#
13.11.2019837.12 Кб9Glava_4.doc
#
11.11.201932.26 Кб2Great Britain.doc
#
14.02.2015667.99 Кб193Gurova_TIZ.pdf
#
14.02.20151.71 Mб36hrestom-filos.pdf