Характеристики нормального розподілу

1. Математичне сподівання (очікування) випадкової величини – це таке її значення, навколо якого групуються результати окремих спостережень.

Математичне сподівання дискретної випадкової величини М(х) визначається, як сума добутків всіх можливих значень випадкової величини на ймовірність появи цих значень:

. (7.26)

Для неперервних випадкових величин воно визначається як

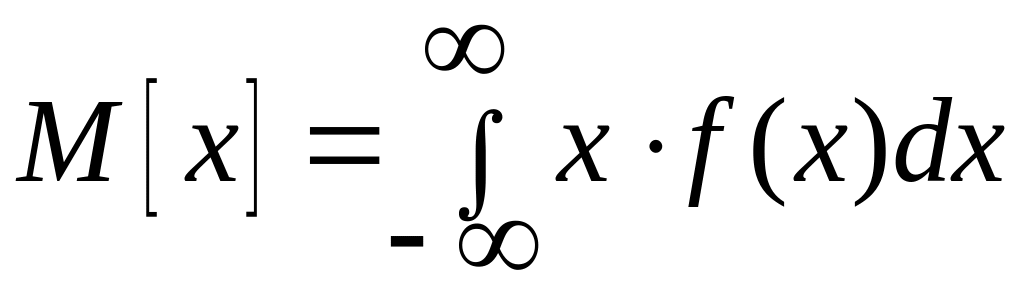. (7.27)

Зазначимо, що математичне очікування дорівнює середньому арифметичному значенню.

Вираз (7.27) означає що математичне сподівання неперервної випадкової величини дорівнює сумі нескінченно великої кількості добутків всіх можливих значень випадкової величини х на нескінченно малі площі f(x)dx, де f(x) – ордината для кожного значення х, а dx – відрізки вісі абсцис.

Якщо спостерігається нормальний розподіл випадкових похибок, то математичне сподівання випадкової похибки дорівнює нулю (рис.7.6).

Якщо ж розглядати нормальний розподіл результатів вимірювань (рис.7.5), то математичне сподівання буде відповідати істинному значенню вимірюваної величини, яке ми позначаємо через „а”.

Похибка вимірювання Δ = х_i - а в загальному випадку може містити дві складові – випадкову і систематичну: ∆=∆_в +∆_с. Характер залежності функції густини ймовірності від значення фізичної величини х і від значення її похибки Δ один і той же ( лише максимум розподілу f(Δ) зміщений вліво по вісі абсцис на величину „а”).

Враховуючи вираз (7.27) і однакову ймовірність виникнення випадкових похибок протилежних знаків і, отже рівність нулю їх математичного сподівання = 0, отримуємо для похибки Δ математичне сподівання у вигляді:

(7.28)

Ми одержали, що математичне сподівання похибки вимірювання дорівнює систематичній похибці.

Виходячи з виразу математичного сподівання можна дати більш чітке визначення систематичної та випадкової похибок.

Систематична похибка Δ_с – це відхилення математичного сподівання результатів вимірювань від істиного значення „а” вимірюваної величини:

(7.29)

Випадкова похибка Δ_в – це різниця між результатом одиночного вимірювання і математичним сподіванням результатів:

(7.30)

Істинне значення вимірюваної величини тоді дорівнює:

(7.31)

2. Дисперсія розподілу випадкових похибок дорівнює дисперсії розподілу результатів вимірювань і характеризує їх розсіювання відносно математичного сподівання.

Зобразимо декілька кривих нормального розподілу випадкових похибок (рис.7.7). Як ми говорили вище, вся площа під кривою розподілу для будь-якої кривої дорівнює 1.

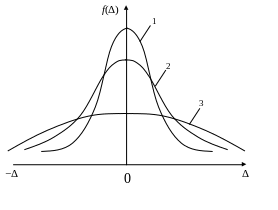
Рис. 7.7. Криві нормального розподілу випадкових похибок:

1- σ = 0,5а; 2 – σ = 1а; 3 – σ = 2а.

Це пов’язано з тим, що крива охоплює всі значення випадкової величини, тобто всі результати спостережень, а сума імовірностей будь-якого із всіх можливих результатів дорівнює 1.

Отже постає питання: як можна характеризувати криві нормального розподілу, рівні по площі, яку вони обмежують, і різні по вигляду?

Порівнюючи між собою криві на рис.7.7 бачимо, що для кривої 1 майже вся площа зосереджена біля ординати, яка відповідає ∆ = 0. Це

значить, що більшість результатів мало відрізняються від математичного сподівання, тобто більшість похибок мало відрізняються від 0. В цьому випадку розсіювання (або розкиданість) результатів спостережень мале, і існує велика ймовірність появи значень, близьких до математичного сподівання.

Розподіл 2 характеризується більшим розсіюванням. Тут ймовірність появи великих похибок зросла, але і відповідно зменшилась ймовірність появи похибок, близьких до 0.

Розсіювання для розподілу 3 ще більше; ймовірність появи великих похибок помітно більша, ніж в розподілі 2.

Для характеристики таких кривих розподілу (рис. 7.7) вводиться параметр – міра розсіювання. Мірою розсіювання значень випадкової величини є дисперсія D = σ².

Для дискретних (теоретичних) розподілів дисперсія відхилень від математичного сподівання визначається виразом:

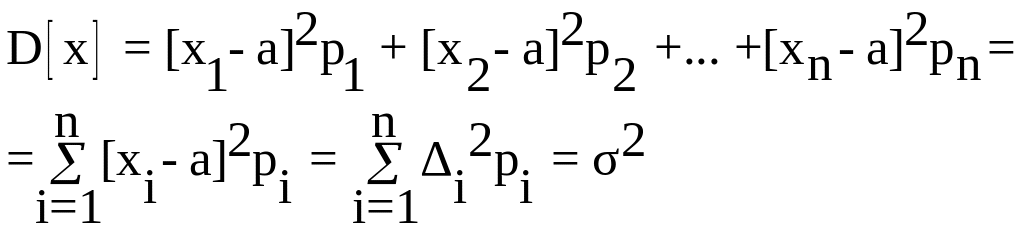(7.32)

Для неперервних випадкових величин:

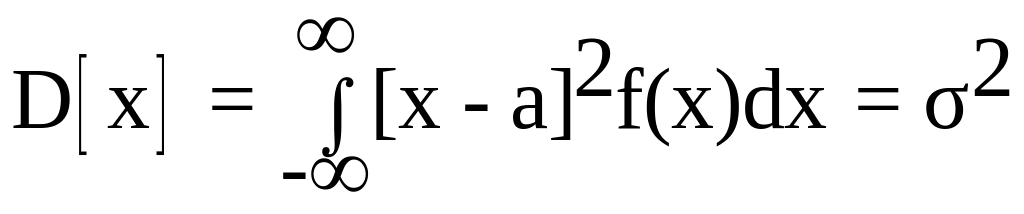(7.33)