7.3. Закони розподілу випадкових величин.

7.3.1. Дискретні і неперервні випадкові величини.

Дискретною випадковою величиною називається така величина, можливі значення якої уявляють собою скінчену або нескінченну послідовність чисел.

Наприклад, можливе число очок при киданні кубика, тобто 1,2,3,4,5,6; можливе число попадань в ціль при ста пострілах: 0,1,2,...99,100. і т.д.

Проміжки між значеннями дискретних величин не заповнені, тобто при киданні кубика не може випасти 2,5 або 3,25 і т.д.

Неперервною випадковою величиною називається величина, можливі значення якої утворюють неперервний ряд чисел.

Можливі значення неперервних величин заповнюють будь-який проміжок без розривів і скачків.

Наприклад, неперервними величинами є довжина відрізку лінії, проміжок часу, інтервал температури і т.д.

Більшість вимірюваних величин ми вважаємо неперервними. В ряді випадків це пов’язано з недостатньою чутливістю засобів вимірювань, які не дають можливості виконувати вимірювання шляхом підрахунку окремих частинок.

З іншого боку, неперервні величини іноді уявляють штучно як дискретні.

7.3.2. Розподіл дискретних величин.

Для повної характеристики дискретної випадкової величини необхідно і достатньо знати можливі її значення і ймовірність появи кожного з цих значень.

Математичний вираз, який дає зв’язок між можливими значеннями випадкової величини і відповідними імовірностями їх появи, називається законом розподілу випадкових величин.

Якщо випадкова величина х приймає ряд дискретних значень , то найбільш проста форма такого закону розподілу –

це задання можливих значень величин імовірностей для кожного дискретного значення випадкової величини: р(х = х₁), р(х = х₂), р(х =х₃), ..., р(х = х_n). При цьому в загальному випадку х_i можуть набувати будь-яких значень, а на величину р(х= х_i) накладаються два обмеження:

1). 0 ≤ р( х = х_i) ≤ 1

(7.10)

2). р(х = х₁) + р(х = х₂) + р(х = х₃) + ... + р(х = х_n) = 1

або

, де р_i = р(х =х_i) (7.11)

В загальному випадку, позначив значення дискретної випадкової величини в порядку їх зростання через х₁, х₂, х₃, ..., х_n, а відповідні їм ймовірності через р₁, р₂, р₃, ..., р_n, одержимо таблицю 7.1.

Таблиця 7.1.

Ряд розподілу дискретної випадкової величини.

х1	х2	х3	х4	. . .	хn
р1	р2	р3	р4	. . .	рn

Така таблиця, якщо вона охоплює всі можливі значення дискретної випадкової величини, дає закон розподілу дискретної випадкової величини. Таблиця 7.1 називається рядом розподілу, який можна представити у вигляді графіка.

Припустимо, що інтервали між сусідніми значеннями рівні між собою, тобто . Тоді графік виглядатиме так, як показано на рисунку 7.1.

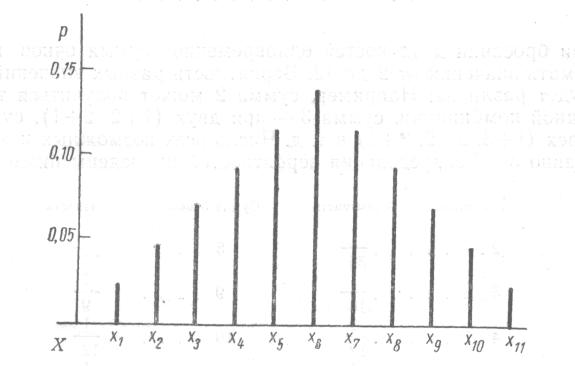
Рис. 7.1. Графік розподілу дискретної випадкової величини.

Сума всіх ординат дорівнює 1. Ми можемо взяти будь-який інтервал (наприклад, х₁ – х₄) і визначити ймовірність того, що значення х лежить в його межах, просумувавши ординати графіка в межах заданого інтервалу, тобто

(7.12)

В ряді випадків розподіл дискретних випадкових величин може виражатися математично. До них належать біномінальний розподіл, розподіл Пуасона та інші.