7.3.3. Розподіл неперервних випадкових величин.

Неперервні величини характеризуються нескінченною множиною можливих значень. Скласти таблицю всіх можливих значень та імовірностей їх появи не можна, оскільки кількість їх в будь-якому інтервалі безмежна.

Однак і в даному випадку існує закон розподілу випадкових величин, але форма його відрізняється від закону розподілу дискретних випадкових величин. Найбільш універсальним способом опису неперервних випадкових величин є знаходження їх інтегральних або диференціальних функцій розподілу.

Коли ми маємо справу з неперервними випадковими величинами, часто нас цікавить не ймовірність р(х) появи певного конкретного значення х, а ймовірність події р( < х), що вимірювана величина прийматиме значення, менші за х. Ця ймовірність є деякою функцією

р( < х) = F (х), (7.13)

де х_i – довільне наперед задане значення величини х.

Функція F(х) називається функцією розподілу ймовірності неперервної випадкової величини, або інтегральною функцією розподілу неперервної випадкової величини.

Отже, під інтегральною функцією розподілу результатів вимірювань слід розуміти залежність ймовірності того. що результат вимірювання в i–вому досліді буде меншим деякого значення Х від самої величини х:

< ) (7.14)

Графік однієї з можливих інтегральних функцій розподілу F(х) для неперервної випадкової величини має наступній вигляд (рис.7.2):

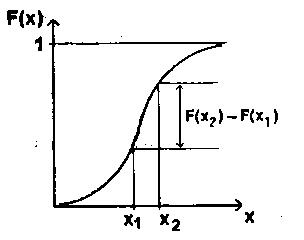Рис. 7.2. Інтегральна функція розподілу для неперервної випадкової величини.

Основні властивості функції F(х):

1. F(х) ≥ 0, тобто F(х) не може приймати від’ємні значення (як і будь-яка ймовірність).

2. Якщо х₂ > х₁, то F (x₂) > F(x₁), тобто F(х) неспадна функція свого аргументу.

3. F( - ∞) = 0, тобто р(х < - ∞) = 0.

4. F( + ∞) = 1.

Виходячи із властивостей функції F(х), знайдемо ймовірність того, що вимірювана величина прийме значення в інтервалі від х₁ до х₂ (х₂ > х₁). Із теореми про додавання імовірностей незалежних подій випливає, що

р(х < х₂) = р(х ≤ х₁) + р(х₁ < х < х₂). (7.15)

Із врахуванням (7.14) одержуємо

р(х₁ < х < х₂) = р(х < х₂) - р(х ≤ х₁) = F (x₂) - F(x₁). (7.16)

Далі, знайдемо ймовірність того, що вимірювана величина прийме конкретне значення, наприклад, х₁, тобто визначимо р(х = х₁). Для цього знайдемо граничне значення (7.16)

p(x₁< x < x₂) = [F (x₂) - F(x₁)] = p(x = x₁). (7.17)

Якщо F(х) в точці х = х₁ не терпить скачка і є неперервною диференційованою функцією, що є характерним для функції розподілу неперервних випадкових величин, то із (7.17) випливає

р(х = х₁) = 0 (7.18)

Отже, ймовірність появи при вимірюванні будь-якого конкретного значення неперервної випадкової величини дорівнює нулю. У цьому випадку має зміст говорити про ймовірність попадання конкретного значення вимірюваної величини лише в певний інтервал значень х, наприклад, від х₁ до х₂ , але х₁ ≠ х₂.

Щоб виявити розподіл імовірностей неперервної випадкової величини, розглядають ряд інтервалів значень величини і підраховують частоти (ймовірності) попадання значень величини на кожний інтервал.

Нехай І_і – ряд інтервалів значень величини х.

р_і - частота попадання значень величини х в і-тий інтервал.

Можна побудувати таблицю, в якій приведено інтервали в порядку їх розташування вздовж вісі абсцис і відповідні частоти попадання значень величини в дані інтервали (таблиця 7.2). Така таблиця називається статистичним рядом.

Таблиця 7.2.

Статистичний ряд неперервної випадкової величини.

Іі	х1;х2	х2;х3	х3;х4	. . .	хn-1;хn
рі	р1	р2	р3	. . .	рn-1

Статистичний ряд графічно представляється в вигляді сходинкової кривої – гістограми (рис.7.3).

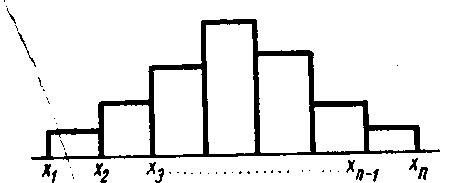
Рис. 7.3. Гістограма.

По вісі абсцис відкладаються інтервали, які є основою прямокутників. Площі прямокутників дорівнюють частотам відповідних інтервалів, тобто імовірностям попадання величини х в даний інтервал.

Таким чином, висота кожного прямокутника дорівнює частоті, поділеній на довжину інтервалу; лише при рівних інтервалах висоти пропорційні відповідним частотам, тобто імовірностям. Зі способу побудови гістограми випливає, що повна площа її дорівнює 1.

Якщо взяти дуже малі інтервали (від х_к до х_к + dx ), то при зменшенні dx крива втратить сходинковий характер і перейде у плавну

криву, яка описується функцією

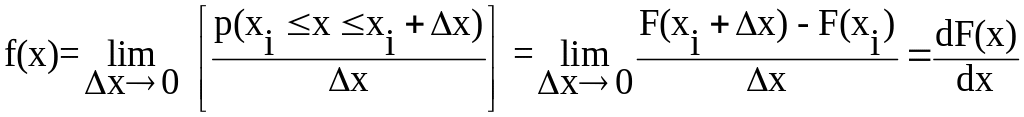(7.19)

Функція f(x) в формі (7.19) називається густиною ймовірності неперервної випадкової величини або диференціальною функцією розподілу ймовірностей. Диференціальна функція розподілу є похідною від інтегральної за своїм аргументом.

Крива f(x) називається кривою розподілу густини ймовірності для даної неперервної випадкової величини, а рівняння, яке її описує – законом розподілу випадкової величини.

Графік диференціальної функції розподілу має дзвіноподібну форму з максимумом при (рис.7.4).

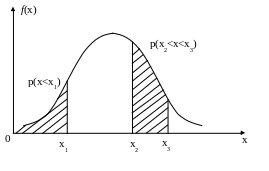
Рис. 7.4. Графік функції розподілу густини ймовірності випадкової неперервної величини

Значення функції f(x) в будь-якій точці називається густиною ймовірності в даній точці. Оскільки інтегральна функція , то справедлива рівність

. (7.20)

Таким чином площа, обмежена кривою диференціальної функції розподілу і віссю абсцис дорівнює 1, тобто ймовірність появи будь-якого з можливих значень дорівнює одиниці. Це означає, що функція f(x) нормована на одиницю.

Вираз називається елементом ймовірності. Він дорівнює ймовірності того, що випадкова величина х може прийняти деяке значення в інтервалі . Тому по формі кривої розподілу можна сказати про те, які інтервали значень випадкової величини більш чи менш імовірні. Для кривої розподілу випадкових величин, показаної на рис.11, більш імовірні значення, які лежать навколо .

Із виразу (7.19) випливають наступні рівності:

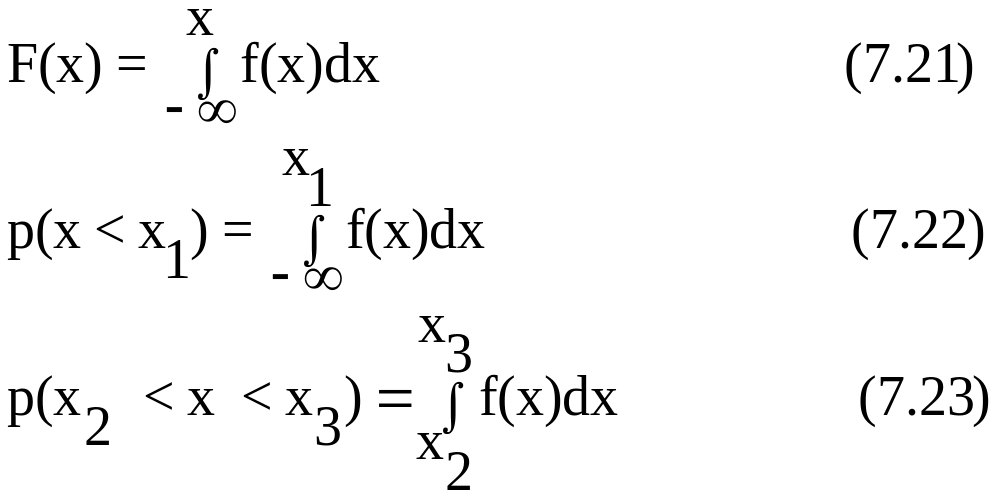
Крім умов (7.20) - (7.23) функція f(x) повинна задовольняти також наступним умовам:

1. ;

2. ;

3. .

Щоб визначити, яка ймовірність того, що значення х буде знаходитися в межах х₂ – х₃, визначають площу між вертикалями з точок х₂ і х₃ (заштрихована площа на рис.7.4). Ця площа пропорційна ймовірності для інтервалу х₂ – х₃

Результати спостережень при багаторазових вимірюваннях можна розглядати як результати спостережень над деякою випадковою величиною.

Маючи ряд результатів можна побудувати гістограму, яка дає уявлення про характер розподілу випадкової величини (рис.7.3).

При збільшенні числа вимірювань і зменшенні інтервалів гістограма наближається до плавної кривої, яка, як ми побачимо далі, характеризує один з теоретичних розподілів неперервних випадкових величин.