6.3. Составные квадратурные формулы с постоянным шагом

Итак, если длина интервала [a, b] области определения функции f(x) велика для применения простейших квадратурных формул, то поступают следующим образом:

1) интервал [a, b] разбивают точками x_i, 0  i  n, на n интервалов по некоторому правилу;

2) на каждом частичном интервале [x_i, x_i+1] применяют простейшую квадратурную формулу и находят приближенное значение интеграла

0  i  n;

3) из полученных выражений I_i составляют квадратурную формулу для всего интервала [a, b];

4) абсолютную погрешность R составной формулы находят суммированием R_i.

Для реализации данного алгоритма разобьем интервал [a, b] на частичные интервалы [x_i, x_i+1] по следующему правилу: x_i+1–x_i = h, 0  i  n – 1, x₀ = a, x_n = b.

Шаг определяется равенством h = (b – a)/n.

6.3.1. Составная формула прямоугольников (средних)

Изобразим рассмотренное правило разбивки (рис. 6.5).

Рис. 6.5

Тогда (6.10) для каждого интервала будет иметь вид

, (6.18)

где x_i  _i  x_i+1, 0  i  n – 1.

Суммирование по i приводит к составной формуле прямоугольников:

I_П = ; (6.19)

где ;   [a, b].

6.3.2. Формула трапеций

Обозначим значение функции f(х) в точках x_i : f_i = f(х_i), i = (рис. 6.6).

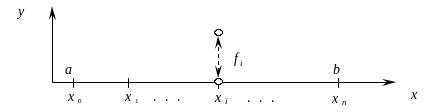
Рис. 6.6

Тогда по аналогии с формулой для прямоугольников из (6.12) получим составную квадратурную формулу трапеций:

I_Т = , (6.20)

где ,  [a, b].

6.3.3. Формула Симпсона

Разобьем интервал [a, b] на четное число частичных интервалов 2m (рис. 6.7), где 2m = (b – a)/h.

Рис. 6.7

Суммируя (6.16)

,

получаем формулу Симпсона:

I_C = , (6.21)

где 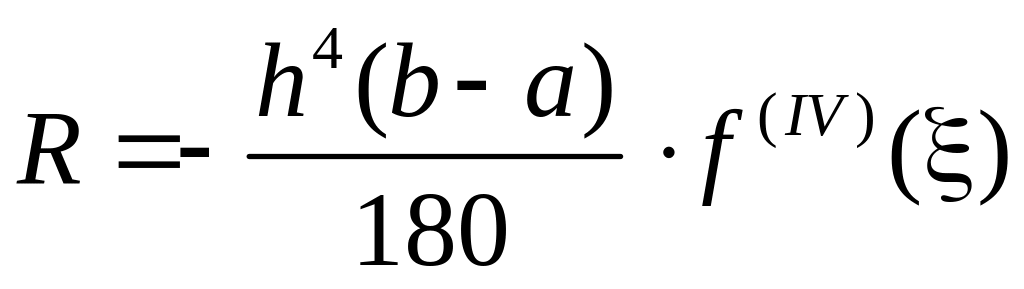,   [a, b].

Заметим, что в отличие от простейших формул при оценке их погрешности в составных формулах (6.19), (6.20) и (6.21) нахождение точки   [a, b] однозначно неопределенно.

На примере (6.1) можно оценить точный выбор точки  для рассчитанных выше составных формул для интервала [a, b].

Пример 6.1. Вычислить интеграл с помощью трех квадратурных формул и сравнить ответ с точным значением I = e – 1 = 1,7182818.

Возьмем произвольно h = 0,1. Тогда

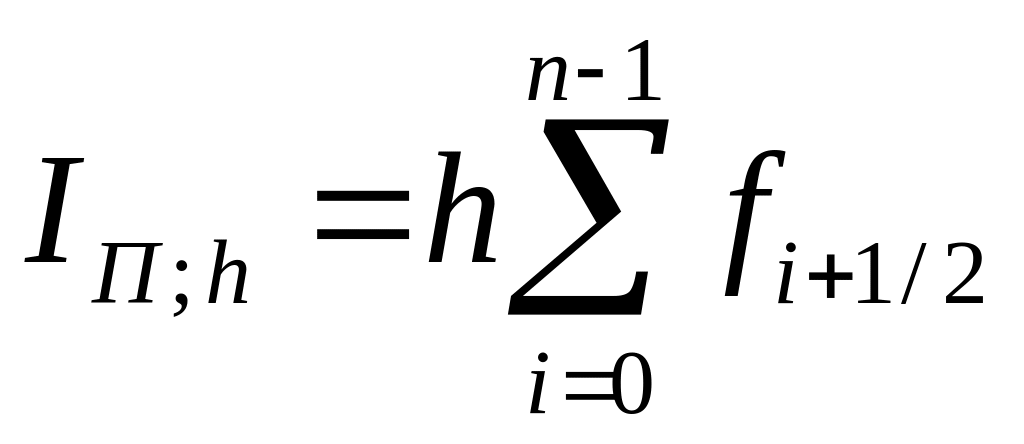= 0,1(e^0,05 + e^0,15 + e^0,25 + e^0,35 + e^0,45 + e^0,55 + e^0,65 +

+ e^0,75 + e^0,85 + e^0,95) = 1,7176;

= 0,05[e^0,0 + 2(e^0,1 + e^0,2 + e^0,3 + e^0,4 +

+ e^0,5 + e^0,6 + e^0,7 + e^0,8 + e^0,9) + e¹] = 1,7197;

= 0,1/3[e^0,0 + 4(e^0,1 + e^0,3 +

+ e^0,5 + e^0,7 + e^0,9) + 2(e^0,2 + e^0,4 + e^0,6 + e^0,8) + e¹] = 1,7182828.

Точное значение I позволяет определить точки  для формул, соответствующих погрешностям R в (6.19), (6.20), (6.21):

 = 0,365;

 = 0,532;

 = 0,588.

Следовательно, для каждой квадратурной формулы следует выбирать свое  с точки зрения оценки точности, что связано с очевидными расчетными трудностями. Утверждение, что повышение точности вычисления интеграла напрямую связано с уменьшением шага h, также не совсем верно.

Из практики известно, что начиная с некоторого n₀ (рис. 6.8) погрешность вычислений снова начинает увеличиваться по причине округлений малых величин.

EMBED Word.Picture.8

Рис. 6.8

В общем случае погрешность интегрирования может быть представлена в виде

,

где q_i – абсолютная погрешность весов; _i – абсолютная погрешность узлов; R – погрешность квадратурной формулы.

В связи с вышеизложенным при вычислении интеграла для выбранной формулы численного интегрирования по заданной точности  выбор шага h производится из следующих соображений:

(6.22)

Соотношения (6.22) означают, что шаг h, а следовательно, и число точек n, в которых вычисляется f(x), определяется значением x с наихудшим поведением f(x) с точки зрения погрешности R.

Однако такое правило разбиения интервала интегрирования может приводить к избыточным вычислениям, если f(x) имеет только частные интервалы с ее «плохим» поведением относительно длины отрезка [a, b].

Д ля примера рассмотрим подынтегра­льную функцию типа f(x) = e^–x/ на отрезке [0, 1] (рис. 6.9) с шагом h = . Очевидно, что согласно (6.22) шаг очень мал для обеспечения заданной точности для всего отрезка [0, 1], т. е. возникает потребность для устранения избыточных вычислений разбивать интервал [a, b] на частичные интервалы различной длины, которая определяется свойствами f(x) и заданной точностью интегрирования.

Таким образом, возникает задача применения простейших квадратурных формул интегрирования с переменным шагом интегрирования на отрезке [a, b].