3.2.2. Графическое отделение корней

Очевидно, что найти корень уравнения (3.1) означает найти абсциссу точки пересечения графика y = f(x) с прямой у = 0, т. е. с осью абсцисс. При этом если построение y = f(x) затруднительно, то ее представляют в эквивалентном виде:

f₁(x) = f₂(x) (3.3)

с таким расчетом, чтобы графики y₁ = f₁(x) и y₂ = f₂(x) строились проще. Абсциссы их точек пересечения и будут корнями уравнения (3.1).

Рассмотрим в качестве примера уравнение x³ – 3x – 0,4 = 0. Согласно (3.3) запишем его как

x³ = 3x + 0,4. (3.4)

Из рис. 3.2 видно, что на отрезке [–3, 3] уравнение (3.4) имеет три корня: с₁  [–2, –1]; с₂  [–1, 0]; с₃  [1, 2].

При графическом отделении корней результат зависит от точности построения графиков уравнений.

EMBED Word.Picture.8

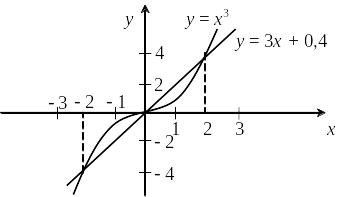
Рис. 3.2

3.3. Итерационные методы уточнения корней

3.3.1. Метод простой итерации

Метод простой итерации применяется к решению уравнения (3.1), разрешенному относительно x:

x = (x). (3.5)

Переход от записи (3.1) к эквивалентной записи (3.5) можно сделать многими способами.

Метод состоит в построении последовательности (3.2) в виде

, n = 0, 1, 2, … .

Если (x_n) – непрерывная функция, а x_n – сходящаяся последовательность, то искомое значение x^* = x_n и будет решением (3.5), следовательно, и (3.1).

Например, получим (3.5) из (3.1) следующим образом: умножим (3.1) на подобранную функцию (x)  0 (в частности можно взять (x) = const) и сложим с тождеством x = x, тогда (3.5) будет иметь вид, эквивалентный виду (3.3):

. (3.6)

Подбирая (x), добиваются сходимости решения (3.6). Функция (x) может быть монотонной, если '(x) > 0, или колеблющейся, если '(x) < 0.

Метод является одношаговым (m = 1), и для начала вычислений нужно знать одно начальное приближение: x₀ =  (рис. 3.3, а), или x₀ =  (рис. 3.3, б), или x₀ = ( + )/2.

В методе простой итерации сходимость гарантирована не всегда, например, если (x) имеет вид, представленный на рис. 3.4.

Представленная ситуация, при которой мы удаляемся от искомого корня, может быть устранена подбором (x) в (3.6).

В качестве (x) можно взять, например, (x) = const = 1/k. При этом необходимо, чтобы |k| > max| f (x)|/2, а знак k должен совпадать со знаком f (x).

EMBED Word.Picture.8

Рис. 3.3

Рис. 3.4

Доказано, что в общем случае расходимость (несходимость) исключается, если подбирается соотношение

| '(x) |  q < 1. (3.7)

При этом скорость сходимости увеличивается при уменьшении величины q.

Максимальный интервал (, ) при выполнении условия (3.7) называется областью сходимости. Для данной оценки (3.7) берется любое значение x  (,); x^*  (, ).

Итерационный процесс уточнения корня заканчивается, когда

| x_n – x_n–1| < , или | f(x_n) – f(x_n–1)| < .

3.3.2. Метод Ньютона (метод касательных)

Данный метод является модификацией метода простой итерации. Если функция f(x) непрерывна и дифференцируема, то, положив в (3.6) , получим эквивалентное уравнение x = x – f(x) / f '(x) = (x), f '(x)  0.

Подбором (x) добиваются, чтобы в (3.7) q = '(x^*)  0, что обеспечивает большую скорость сходимости в рекуррентном соотношении метода Ньютона вблизи искомого корня:

, n = 1, 2, … . (3.8)

Это также одношаговый метод.

Геометрическая интерпретация метода представлена на рис. 3.5.

EMBED Word.Picture.8

Рис. 3.5

Проблематичным является выбор x₀ ввиду узости области сходимости вычисления производной. Часто при неудачном выборе x₀ нет монотонного убывания последовательности | f(x_n) |, поэтому рекомендуется вычисления проводить по модифицированной схеме:

n = 0, 1, 2, … .

Сомножители _n  [0, 1] выбирают так, чтобы выполнялось неравенство

| f(x_n+1)| < | f(x_n)| .

При выборе начального приближения х₀ предпочтительней использовать заведомо сходящийся метод, например метод деления отрезка пополам.