Локальная интерполяция. Рассмотрим два вида локальной интерполяции – линейную и квадратичную.

1. Линейная интерполяция:

y = a_ix + b_i;

a_i = (y_i – y_i–1)/(x_i – x_i–1); b_i = y_i–1 – a_ix_i–1;

x_t = 0,4; 0,3  x_t 0,5; x_i–1 = 0,3; x_i = 0,5;

y_i–1 = 0,2; y_i = 1;

a₃ = (1 – 0,2)/(0,5 – 0,3) = 0,8/0,2 = 4; b₃ = –1;

y = 4x – 1, при x = 0,4; y = 40,4 – 1 = 0,6. (5.28)

2. Квадратичная интерполяция:

y = a_ix² + b_ix + c_i.

Выбираем три ближайшие точки к x_t = 0,4:

x_i–1 = 0,1; x_i = 0,3; x_i+1 = 0,5.

y_i–1 = 0; y_i = 0,2; y_i+1 = 1.



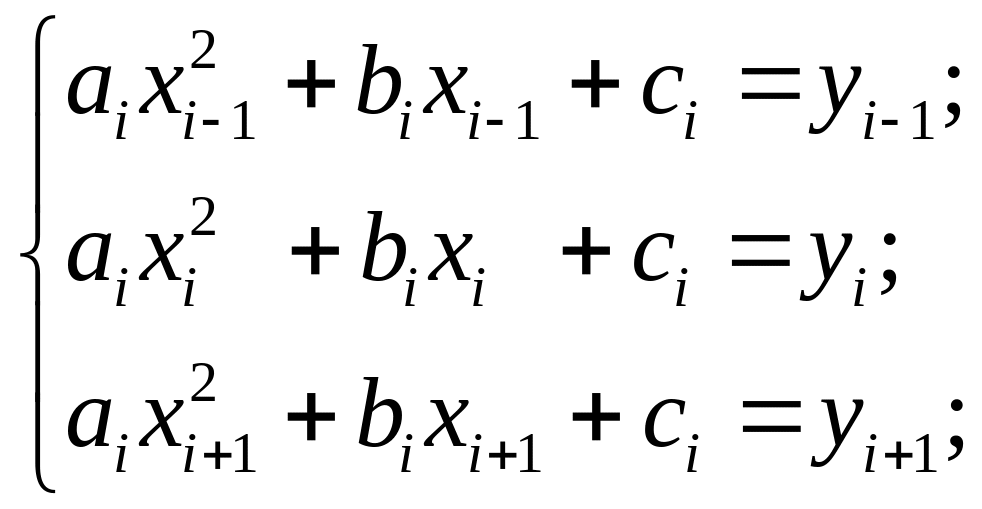
A = 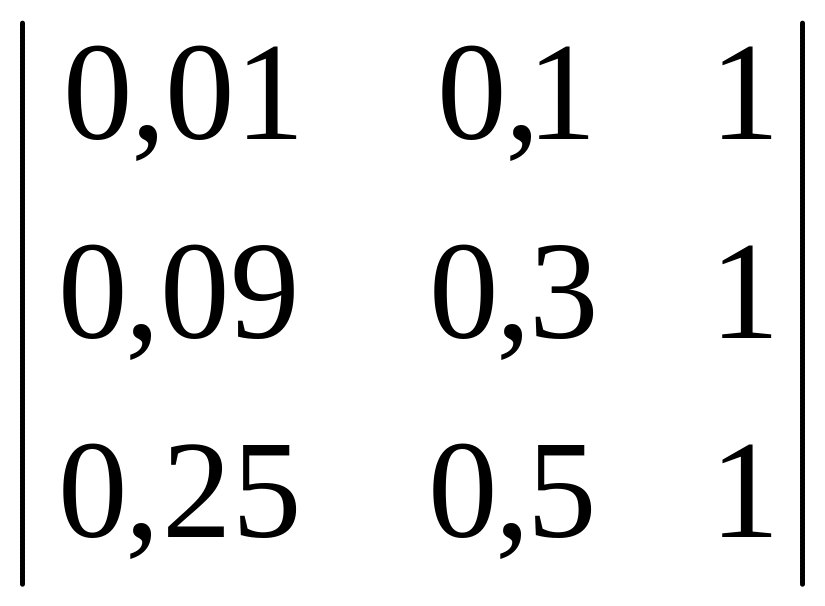; = ; = =A^–1 .

Найдем A^–1 = ; = =  ;

a = 0 – = 7,5; b = –2; c = 0,125;

y = 7,5x² – 2x + 0,125 при x = 0,4; y = 0,525. (5.29)

Глобальная интерполяция. Рассмотрим интерполяционные многочлены Лагранжа и Ньютона.

1. Интерполяционный многочлен Лагранжа:

L(x) = ;

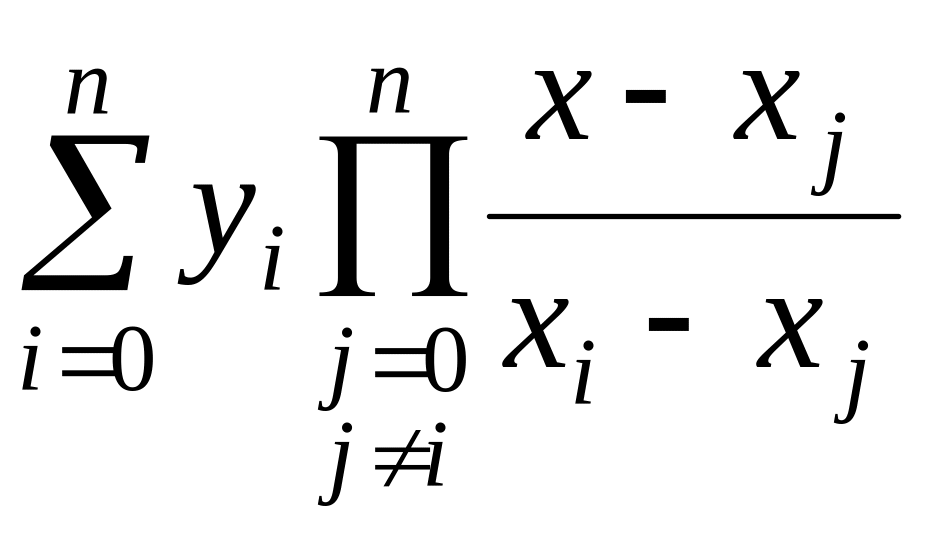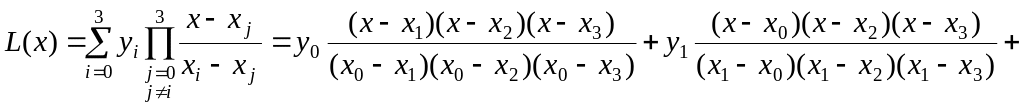
при x = 0,4; y  L(x) = 0,3999.

Найдем выражение для полинома Лагранжа при n = 1 и x_T = 0,4:

что соответствует (5.28).

Для n = 2 и x_T = 0,4, y  L(x) = .

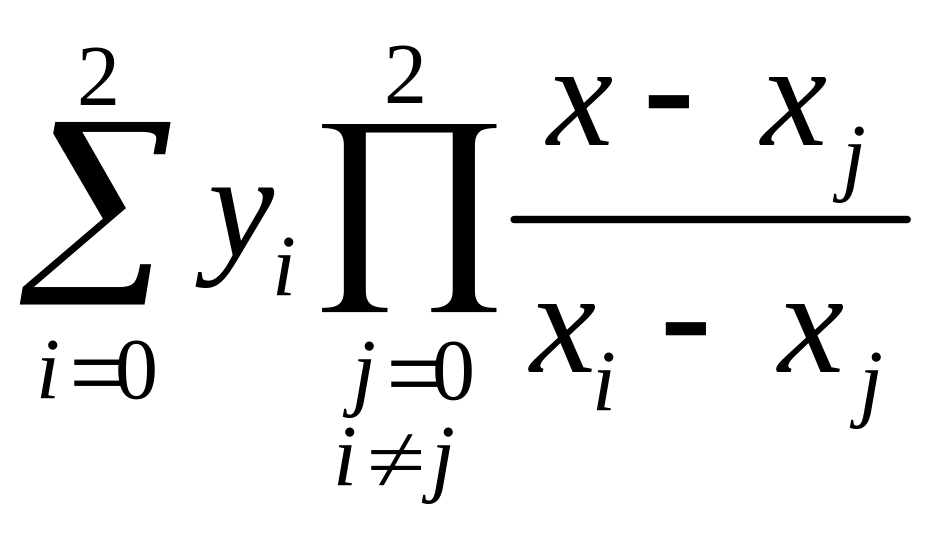Для рассматриваемого интервала [x₁, x₃] берем x₀ = 0,1; x₁ = 0,3; x₂ = 0,5; y₀ = 0; y₁ = 0,2; y₂ = 1. Тогда

y  L(x) = 0,2 ;

что соответствует (5.29).

На рис. 5.4 представлен алгоритм расчета интерполяционного многочлена Лагранжа, реализованный в виде функции PL со следующими параметрами:

x_T – значение текущей точки;

, – одномерные массивы известных значений x и f(x);

n – размер массивов , .

В схеме введены следующие обозначения:

p – значение накапливаемой суммы, результат которой равен L(x_Т);

e – значение очередного члена произведения.

Результатом функции PL является значение p.

2. Интерполяционный многочлен Ньютона рассмотрим для случая неравноотстоящих узлов при n = 3:

N₃(x) = f(x₀) + (x – x₀)f(x₀, x₁) + (x – x₀)(x – x₁) f(x₀, x₁, x₂) +

+ (x – x₀)(x – x₁)(x – x₂) f(x₀, x₁, x₂, x₃).

По схеме табл. 5.2 находим раздельные разности:

f(x₀, x₁) = ;

f(x₁, x₂) = ;

f(x₂, x₃) = ;

f(x₀, x₁, x₂) =

f(x₁, x₂, x₃) =

f(x₀, x₁, x₂, x₃) = .

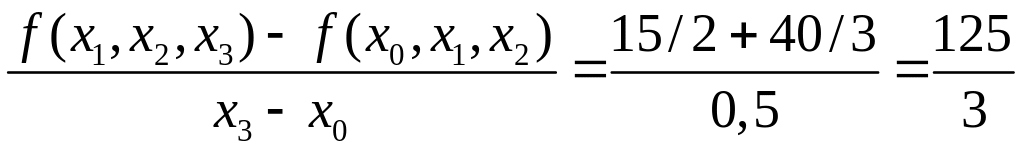Рис. 5.4

Результаты расчетов поместим в табл. 5.3:

Таблица 5.3

n	xn	fn	f(xn, xn+1)	f(xn, xn+1, xn+2)	f(xn, xn+1, xn+2, xn+3)
0	0	–0,5
1	0,1	0	5	–40/3	125/3
2	0,3	0,2	1	15/2
3	0,5	1	4

Используя первые в столбцах разделенные разности, получаем

N₃(x) = –0,5 + (x – 0)5 + (x – 0)(x – 0,1)(– 40/3) +

+ (x – 0)(x – 0,1)(x – 0,3)125/3 = x³ – 30x² + x – 0,5. (5.30)

Напомним, что расчеты интерполяционного многочлена Ньютона выполняются по формуле

,

где x_T – текущая точка, в которой нужно вычислить значение многочлена; – разделенные разности порядка k, которые вычисляются по следующим рекуррентным формулам:

Схема алгоритма расчета многочлена Ньютона, реализованная в виде функции PN с параметрами, значения которых аналогичны рассмотренной ранее функции PL, представлена на рис. 5.5. Результатом функции PN является значение N.

Рис. 5.5