2.3. Вычисление определителей высоких порядков

Для матриц общего вида, являющихся элементом СЛАУ, для вычисления определителей успешно может использоваться метод Гаусса. Прямой ход метода для системы позволяет вычислить

,

так как последовательное исключение элементов величину определителя не изменяет. Здесь а_kk – элементы преобразованной матрицы А (прямой ход Гаусса). Знак  зависит от четности или нечетности перестановок строк исходной матрицы при приведении ее к треугольному виду.

Для симметричных матриц

; .

2.4. Вычисление обратных матриц

1. По методу Гаусса. Всякая неособенная матрица, для которой , имеет обратную матрицу. Очевидно, что АА^–1 = Е. Запишем это равенство в виде системы n уравнений с n неизвестными:

, (2.38)

где а_ik – элементы матрицы А; z_kj – элементы обратной матрицы А^–1; _ij – элементы единичной матрицы. При этом _ij =

Для нахождения элементов одного столбца обратной матрицы необходимо решить соответствующую линейную систему (2.38) с матрицей А. Так для получения j-го столбца матрицы А^–1 (z_1j, z_2j, …, z_nj) решается система

(2.39)

Следовательно, для обращения матрицы А нужно n раз решить систему (2.39) при j = . Поскольку матрица А системы не изменяется, то исключение неизвестных выполняется только один раз, а (n – 1) раз при решении (2.39) выполняется только обратный ход с соответствующим изменением ее правой части.

2. Другой подход к определению обратной матрицы А^–1:

,

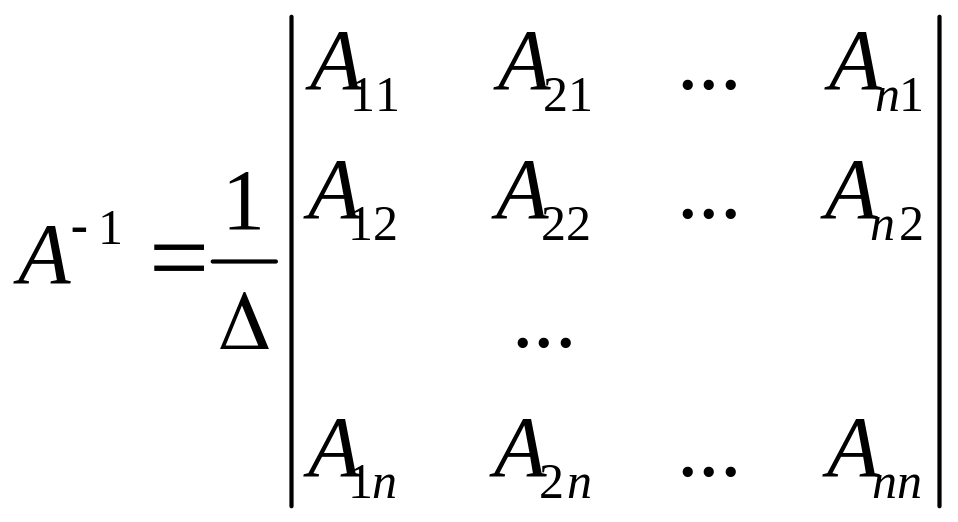где  – определитель матрицы; А_ij – алгебраические дополнения соответствующих элементов матрицы А.

3. Обращение матрицы А посредством треугольных матриц. Известно, что всякая обратная матрица, если она существует, по структуре будет такая же, как и исходная, так как

А^–1А = АА^–1 = Е = . (2.40)

Рассмотрим пример обращения матрицы 3-го порядка следующего вида:

А = . (2.41)

Решение. Матрицу А^–1 ищем в виде

А^–1 = . (2.42)

Перемножив А и А^–1 с учетом (2.40), получим t₁₁ = 1; t₁₁ + 2t₂₁ = 0; 2t₂₂ = 1;

Отсюда последовательно находим t₁₁ = 1; t₂₁ = –1/2; t₃₁ = 0; t₂₂ = 1/2; t₃₂ = –1/3; t₃₃ = 1/3, следовательно,

А^–1 = . (2.43)

Перемножив (2.43) и (2.41), получим (2.40).

Известно, что любая произвольная матрица А может быть представлена в виде двух треугольных. Например, пусть известна матрица

. (2.44)

Будем искать Т₁ = и Т₂ = .

Диагональ в матрице Т₂ искусственно берется равной 1. Тогда

A = T₁  T₂ . (2.45)

Реализовав (2.45) и сравнив с (2.44), получим

= .

Сравнив значения правой и левой частей и выполнив простейшие вычисления, получим

t₁₁ = 1; t₁₁ r₁₂ = –1; t₁₁ r₁₃ = 2;

t₂₁ = –1; t₂₁ r₁₂ + t₂₂ = 5; t₂₁ r₁₃ + t₂₂ r₂₃ = 4;

t₃₁ = 2; t₃₁ r₁₂ + t₃₂ = –1; t₃₁ r₁₃ + t₃₂ r₂₃ + t₃₃ = 14.

Решив полученную систему, получим

t₁₁ = 1; t₂₁ = –1; t₃₁ = 2;

t₂₂ = 4; t₃₂ = 6; t₃₁ = 1;

r₁₂ = –1; r₁₃ = 2; r₂₃ = 3/2.

Таким образом, Т₁ = и Т₂ = , тогда A^–1 = .

2.5. Применение метода итераций для уточнения элементов обратной матрицы

Точность получения элементов обратной матрицы оценивается соотношением

А^–1  А = А⁰ = Е.

Однако в общем случае элементы обратной матрицы получаются с некоторой погрешностью, которая появляется в результате округлений в процессе вычисления и большого числа арифметических операций. Для уменьшения погрешностей используется итерационная схема уточнения элементов обратной матрицы.

Пусть для неособенной матрицы А получено приближенное значение элементов матрицы А^–1. Обозначим ее через D₀  A^–1. Тогда для уточнения элементов обратной матрицы строится следующий итерационный процесс:

F_k–1 = E – AD_k–1; k =1, 2, 3, …; (2.46)

D_k = D_k–1 (E + F_k–1); k = 1, 2, 3, … . (2.47)

Доказано, что итерации сходятся, если начальная матрица D₀ достаточно близка к искомой А^–1.

В данной итерационной схеме матрица F на каждом шаге как бы оценивает близость матрицы D к А^–1.

Схема работает следующим образом.

Сначала по (2.46) при k = 1 находится F₀ = E – AD₀, затем  произведение D₀F₀.

По (2.47) при k = 1 находится D₁ = D₀ + D₀F₀.

Чтобы проверить, достигнута ли желаемая точность, вычисляется AD₁, а по (2.46) при k = 2 вычисляется F₁ = E – AD₁ и, если наибольший элемент матрицы F₁ < , итерации прекращаются, следовательно, A^–1  D₁.