5.5. Сплайны

Пусть интервал [a, b] разбит узлами x_i на n отрезков, 0  i  n. Сплайном S_n(x) называется функция, определенная на [a, b], принадлежащая C^k[a, b] и такая, что на каждом отрезке [x_i, x_i₊₁], 0  i  n – 1 – это полином n-й степени.

В частности, это могут быть построенные специальным образом многочлены 3-й степени (кубический сплайн), которые являются математической моделью гибкого тонкого стержня, закрепленного в двух точках на концах с заданными углами наклона  и  (рис. 5.6).

Рис. 5.6

В данной физической модели стержень принимает форму, минимизирующую его потенциальную энергию. Пусть форма стержня определяется какой-то функцией y = S(x). Из курса сопротивления материалов известно, что уравнение свободного равновесия имеет вид S⁽^IV⁾(x) = 0. Такому состоянию соответствует многочлен третьей степени между двумя соседними узлами интерполяции. Его выбирают в виде

S(x) = a_i+ b_i(x – x_i_–1) + c_i(x – x_i_–1)²+ d_i(x – x_i_–1)³ ; x_i_–1  х  x_i . (5.31)

Следовательно, стоит проблема нахождения a_i, b_i, c_i, d_i. Для их определения на всех элементарных участках интервала [a, b] необходимо составить 4n уравнений. Часть этих уравнений получают из условия прохождения S(x) через заданные точки, т. е.

S(x_i_–1) = y_i_–1; S(x_i) = y_i,

используя (5.31), эти условия можно записать в виде:

(5.32)

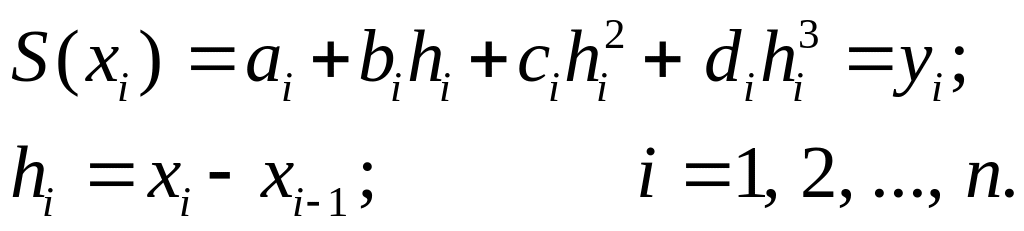(5.33)

Уравнения в количестве (2n – 2) получают из условия непрерывности первых и вторых производных в узлах интерполяции.

Вычислим производные многочлена (5.31):

(x) = b_i+ 2c_i(x – x_i_–1) + 3d_i(x – x_i_–1)²,

(x) = 2c_i+ 6d_i(x – x_i_–1) при x_i_–1 х  x_i . (5.34)

Приравнивая в каждом внутреннем узле x = x_i значения этих производных, вычисленных на концах рассматриваемого отрезка, получают (2n – 2) уравнений:

b_i₊₁= b_i + 2h_ic_i + 3h d_i ; i = 1, 2, …, n – 1; (5.35)

c_i₊₁= c_i + 3h_id_i; i = 1, 2, …, n – 1. (5.36)

Оставшиеся два уравнения получают из естественного предположения условия о нулевой кривизне этой функции на концах отрезка:

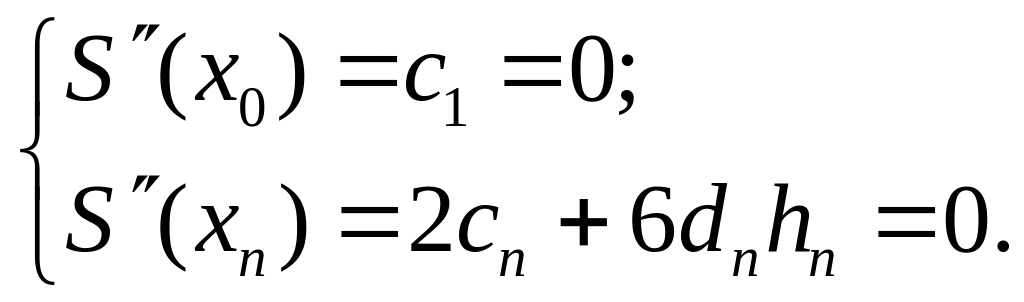(5.37)

Система, составленная из (5.32) – (5.37), решается одним из методов решения СЛАУ.

Для упрощения машинных расчетов эта система уравнений приводится к более удобному виду посредством следующего алгоритма.

1. Из условия (5.32) можно сразу найти a_i.

2. Из (5.36) – (5.37) находят

(5.38)

3. После подстановки (5.38) и (5.32) в (5.33) находят коэффициенты b_i:

(5.39)

4. С учетом (5.38) и (5.39) из уравнения (5.35) исключаются d_i и b_i, тогда исходная система приводится к трехдиагональной матрице, содержащей только коэффициенты c_i. Получаем систему

h_i_–1c_i_–1 + 2 (h_i_–1 + h_i)c_i + h_ic_i₊₁ = 3 , i = 2, 3, …, n. (5.40)

При этом c₁ = 0, c_n₊₁ = 0. Система (5.40) может быть решена методом прогонки. Зная c_i по (5.38) и (5.39), определяют b_i и d_i. Тогда кубический многочлен определяется для всех интервалов.