5.6. Сглаживание результатов экспериментов

Когда невозможно обеспечить чистоту эксперимента при получении табличных значений функции, нужно иметь в виду ошибки этих значений. Интерполирование усугубляет эти ошибки. В этом случае для аппроксимации прибегают к построению эмпирических формул как моделей приближенных функциональных зависимостей. График эмпирических зависимостей не проходит через точки {x_i, y_i}. В результате экспериментальные данные как бы сглаживаются посредством подбора эмпирических формул.

Построение эмпирических формул состоит из двух этапов:

1) построение их общего вида;

2) определение наилучших значений содержащихся в них параметров.

1. Общий вид определяется из физических соображений. Если характер зависимостей неизвестен, то формулы выбираются произвольно, в соответствии с их простотой. Выбор начинают среди простейших функций (из геометрических соображений).

2. Если эмпирические формулы подобраны, то они представляются в общем виде:

y = (x, a₀, a₁, ... , a_m); (5.41)

где  – известная функция; a_i – неизвестные коэффициенты, которые подбираются для лучшего приближения.

Отклонение (невязка) определяется как

_i = (x_i, a₀, a₁, ..., a_m) – y_i; i = . (5.42)

Задача нахождения a_i сводится к минимизации _i. Существует несколько способов нахождения a_i: метод выбранных точек, метод средних, метод наименьших квадратов.

Метод выбранных точек. В системе координат XOY наносится система точек и проводится простейшая плавная кривая или прямая. На проведенной прямой набирается система точек, число которых должно быть равно числу неизвестных коэффициентов в эмпирической формуле. Координаты (х⁰_j, y⁰_j) старательно измеряются и используются для записи условия прохождения через них прямой.

Из следующей системы находят a_i:

; j = .

Метод средних. В данном случае параметры a_i для соотношения (5.41) находятся из условия

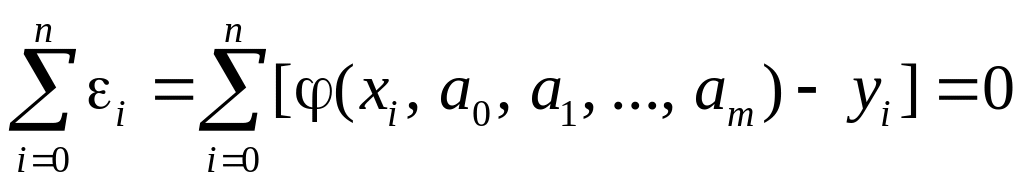. (5.43)

Условно равенство (5.43) разбивают на систему, состоящую из (m + 1) уравнений:

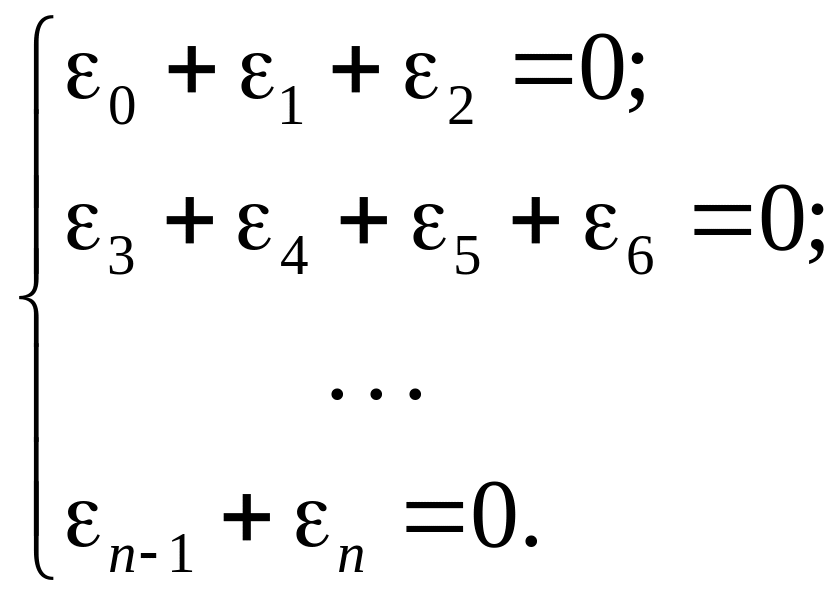(5.44)

Решают систему (5.44) и находят коэффициенты a_i.

Метод наименьших квадратов. В данном случае речь идет о среднеквадратичном приближении аппроксимируемой функции посредством многочлена:

(x) = , (5.45)

при этом m  n; случай m = n соответствует интерполяции. На практике, как правило, m = 1, 2, 3. Мерой отклонения (x) от f(x) на множестве точек (x_i, y_i) (i = 0, 1, …, n) в данном случае является соотношение по невязке:

S = . (5.46)

Параметры а_i как независимые переменные находятся из условия минимума функции S = S(a₀, a₁, …, a_n–1).

Система уравнений

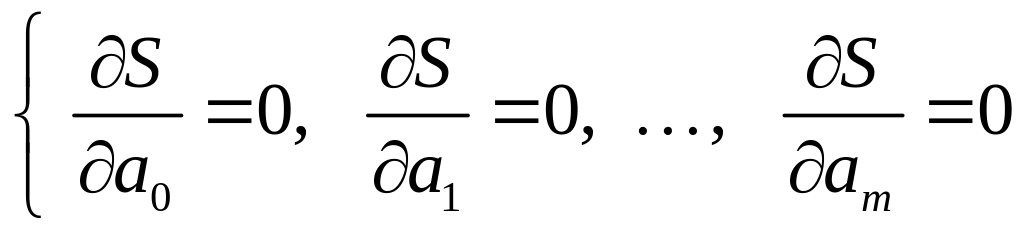, (5.47)

трактуется следующим образом:

= = . (5.48)

Из системы (5.47) определяются параметры a_i. В этом и состоит метод наименьших квадратов (МНК).

5.7. Вычисление многочленов

Из вышеизложенного очевидно, что при аппроксимации очень часто приходится вычислять значения многочленов вида

P(x) = a₀ + a₁x + a₂x² + … + a_nxⁿ . (5.49)

Если выполнять все вычисления, то нужно (n² + n/2) умножений, n сложений и плюс округления при выполнении этих операций. Поэтому для вычисления используют схему Горнера, в которой требуется выполнить только n умножений и n сложений:

P(x) = a₀ + x(a₁ + x(a₂ + …+ x(a_n–1 + xa_n) … )) . (5.50)

Алгоритм реализации вычисления (5.49) согласно формуле (5.50) представлен на рис. 5.7.

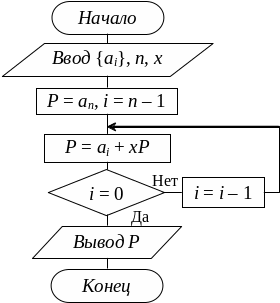
Рис. 5.7