17. Автокорреляционная функция случайного процесса. Примеры автокорр. Функций.

К орреляционные хар-ки явл. наиболее широко применимыми в инженерной практике и в научных исслед., связ. с анализом случ. процессов.

Автокорреляционная функция отражает общую зависимость ординат процесса в данный момент времени от ординат процесса, отстоящего на некоторое время: t₂-t₁=τ.

Автокорреляц. ф-ция: , 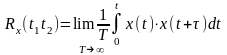.Если t₂-t₁=τ:

С-ва автокорреляц. ф-ции:

1) Эта величина всегда действительная.

2) R_x(τ)= R_x(-τ)

3) R_x(0)≥ R_x(τ) для любого τ

4) R_x(∞)=m_x Хвост автокор. ф-ции стремится к мат. ожиданию.

5

R_x(τ)

) R_x(0)=D_x

Виды автокорреляц. ф-ций:

1)Для гармонического процесса:

x(t)=A₀sinωt

2) Случ. процесс:

3) Смесь: случ. + гармонич.

4)Белый шум

5)Узкополосный процесс

П римеры применения автокор. ф-ций:

1) Фильтры (когда оч. большой период: 11 лет –активность Солнца)

2) Геологич. разведка (полезные ископаемые): отделить шумы,

принимаемые сейсмо-датчиками, при взрыве зарядов.

Кор. ф-цию описывают нек. характеристиками:

- R_x(0)

- задают максимумы и минимумы

- корнями

Кор. ф-ция величина размерная, и значения зависят от единиц измерения.

18. Взаимная корреляционная функция случайных процессов. Примеры применения корреляционных характеристик.

Для оценки статистической связи между двумя процессами используется понятие взаимокорреляционной функции:

Заменим на .

Получим:

Применение:

1) Для определения путей прохождения сигнала

2) Выделение полезного сигнала на уровне помех (Корреляционный приём), когда помеха намного больше сигнала.

Св-ва корреляц. функции:

1) Эта величина всегда действительная.

2) Rx(τ)= Rx(τ)

3) Rx(0)≥ Rx(τ) для любого τ

4) Rx(∞)=mx Хвост автокор. ф-ции стремится к мат. ожиданию.

5) Rx(0)=Dx энергетич.

19. Усреднение по ансамблю и по времени. Эргодическое свойство случайных процессов.

Измерить случ. процесс – определить его статистич. хар-ки, кот. определяются по одной или нескольким реализациям и эти хар-ки отражают с-ва всего процесса. Случ. процесс, набл. за короткий промежуток времени – наз. РЕАЛИЗАЦИЕЙ. Совокупность реализаций случ. процесса наз. АНСАМБЛЕМ.

К хар-кам случ. процесса можно отнести среднее значение квадрата, мат. ожидание, дисперсию, среднеквадрат. отклонение, закон распред-я. Все статистич. хар-тики получ. путём осреднения, при этом осреднение может осущ. осреднением по ансамблю либо осреднению по времени.

Случ. процесс обладает с-вом ЭРГОДИЧНОСТИ, если статистич. хар-ки, найдены осреднением по времени и по ансамблю равны, например, x=∫f{x)Xdx =1/T ∫x{t)dt.

Будем исходить из гипотезы эргодичности и осреднять будем по времени.

. (3)

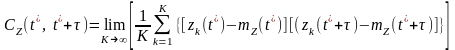. (4)

Формулы (3) и (4) показывают, как можно определить характеристики случайного процесса путем усреднения по ансамблю в определенные моменты времени. Однако в большинстве случаев характеристики стационарного случайного процесса можно вычислить, усредняя по времени в пределах отдельной выборочной функции, входящей в ансамбль. Возьмем, например, k-ую выборочную функцию ансамбля Среднее значение и ковариационная функция , вычисленные по k-ой реализации равны

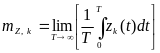, (7 а)

. (7 б)

Если случайный процесс стационарен, а и , вычисленные по различным реализациям согласно формулам (7), совпадают, то случайный процесс называется эргодическим. Для эргодических процессов средние значения и ковариационные функции, полученные усреднением по времени (как и другие характеристики, вычисленные усреднением по времени), равны аналогичным характеристикам, найденным усреднением по ансамблю, т. е. и .

Эргодические случайные процессы образуют очень важный класс случайных процессов, поскольку все свойства эргодических процессов можно определить по единственной выборочной функции. На практике стационарные случайные процессы обычно оказываются эргодическими. Стационарные процессы называются эргодическими, если для них усреднение по времени приводит к тем же результатам, что и статистическое усреднение, т. е. математическое ожидание равно постоянной составляющей, а дисперсии — мощности переменной составляющей. Грубо говоря, эргодичность процесса заключается в том, что все его реализации похожи друг на друга. Эргодические процессы часто используются в качестве математических моделей реальных сообщений, сигналов и помех.

По этой причине свойства стационарных случайных явлений можно определить по одной наблюдаемой реализации.

Особую практическую значимость имеют стационарные процессы, называемые гауссовыми или нормальными процессами. Гауссов случайный процесс характеризуется тем, что совместная плотность распределения величин , определенных для всевозможных временных сечений t, является многомерной нормальной (гауссовой) плотностью. Случайная выборка гауссова процесса, определенная для сечений , описывается N-мерным совместным гауссовым распределением компонент.