
- •1. Передача информации между двумя оконечными устройствами. Тип соединения оконечных устройств
- •2. Основные определения: информация, сообщение, система связи, сигнал, алфавит.
- •3. Обобщенная структура схемы системы связи
- •4. Источники сообщения в системах связи. Вероятностный характер источников сообщений.
- •5. Форматирование информации. Форматирование текстовых данных. Существующие стандарты.
- •6. Передача сообщений по каналу, искажения, краевые искажения, дробление
- •7. Аналоговые источники сообщений. Преобразование аналоговых сигналов в цифровые. Квантование по уровню. Ошибка квантования.
- •8. Дискретизация аналоговых сигналов по времени. Понятие о теореме Котельникова.
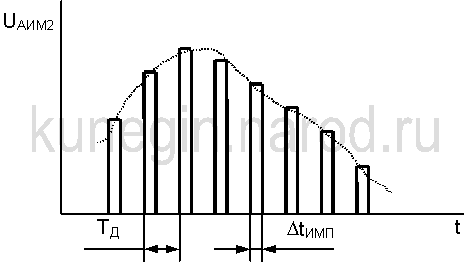
- •9. Преобразование аналоговых сигналов в цифровые. Дискретизация по методу «выборка-хранение». (доработать)
- •10. Сигнал, как реализация процесса. Классификация процессов.
- •11. Классификация процессов. Детерминированные процессы. Гармонические и переходные непериодические процессы.
- •12. Полигармонические и непериодические процессы их спектральные характеристики.
- •13. Определение случайного процесса. Непрерывные и дискретные случайные процессы.
- •14. Измерение случайных процессов.
- •15. Числовые характеристики случайных процессов, их инженерно-физический смысл.
- •16.Законы распределения и основные характеристики случайных процессов
- •17. Автокорреляционная функция случайного процесса. Примеры автокорр. Функций.
- •18. Взаимная корреляционная функция случайных процессов. Примеры применения корреляционных характеристик.
- •19. Усреднение по ансамблю и по времени. Эргодическое свойство случайных процессов.
- •20. Стационарность случайных процессов. Стационарность в широком и узком смыслах.
- •21. Информационные модели сигналов. Формула Хартли.
- •22. Информационные модели сигналов. Формула Шеннона.
- •23. Энтропия источника сообщений. Свойства энтропии источника дискретных сообщений.
- •24. Избыточность при передаче сообщений. Роль избыточности при передаче информации.
- •25. Математические модели сигналов. Временное и частотное представление сигналов.
- •26. Ряд Фурье по произвольной ортогональной системе функций.
- •31. Спектральные характеристики непериодического сигнала. Прямое и обратное преобразования Фурье.
- •32. Оценивание спектральной плотности с помощью дпф
- •33. Дискретное преобразование Фурье (дпф). Гармонический анализ.
- •34. Примеры ортогональных базисов. Функции Уолша.
- •35. Модуляция. Зачем она нужна
- •36. Амплитудная модуляция.Спектр ам сигнала. Примеры модуляторов.
- •37 Амплитудно-модулируемый сигнал сложной формы, его спектр.
- •38 Демодуляция ам сигнала. Работа простейшего амплитудного детектора.
- •43. Спектр колебаний с угловой модуляцией
- •44. Сравнение методов амплитудной и угловой модуляций
- •45. Двоичное представление информации. Механизм восстановления двоичных импульсов.
- •46. Спектральные характеристики случайных процессов.
- •47. Преобразование кодов.
- •48. Корректирующие коды. Ход Хемминга
- •49. Неравномерные коды. Код Хаффмана.
- •50. Неравномерные коды. Код Шеннона-Фано
- •51. Дискретизация аналоговых сигналов по времени. Понятие о теореме котельникова.
- •52. Спектр прямоугольного сиганала
- •53. Свойства энтропии источника дискретных сообщений.
50. Неравномерные коды. Код Шеннона-Фано
Кодирование по методу Шеннона-Фано состоит из следующих этапов:
Подлежащие кодированию символы алфавита источника дискретных сообщений располагают в первом столбце таблицы в порядке убывания вероятностей.
Символы алфавита разбивают на две группы с примерно равными суммарными вероятностями. Символам первой (верхней) группы присваивают 0 в качестве первого знака двоичной кодовой комбинации, а символам второй группы - 1.
Символы, входящие в каждую из групп, вновь разбивают на две группы с примерно равными суммарными вероятностями. Символам вновь полученных первых (верхних) подгрупп присваивают 0 в качестве следующего знака двоичной кодовой комбинации, а символам вторых подгрупп -1.
Пункт 3) продолжают до тех пор, пока в каждой из подгрупп не останется по одному символу.
Все кодируемые символы перечисляются в порядке уменьшения их вероятностей
X*m |
Prob[X*m] |
Код |
Длина Lm |
Prob[X*m] Lm |
||
a |
0.4 |
00 |
2 |
0.8 |
||
b |
0.2 |
01 |
2 |
0.4 |
||
c |
0.2 |
10 |
2 |
0.4 |
||
d |
0.1 |
110 |
3 |
0.3 |
||
e |
0.1 |
111 |
3 |
0.3 |
||
|
Lср=2,2 |
|
||||
Все символы делятся на m примерно равновероятностных групп.
Верхней группе ставится 0, а нижней 1. Затем обе группы снова разделяются на m подгрупп. Такое разделение продолжается до тех пор пока в таблице не исчезнут префиксно зависимые кодовые слова
Н=2,122

51. Дискретизация аналоговых сигналов по времени. Понятие о теореме котельникова.
Дискретизация аналогового (непрерывного) сигнала по времени – представление данного аналогового сигнала в виде последовательности дискретных сигналов (импульсов).

Теорема
Котельникова (в англоязычной
литературе — теорема Найквиста —
Шеннона или теорема отсчётов) гласит,
что, если аналоговый
сигнал ![]() имеет
финитный (ограниченный по ширине) спектр,
то он может быть восстановлен однозначно
и без потерь по своим дискретным отсчётам,
взятым с частотой строго большей'
удвоенной верхней частоты
имеет
финитный (ограниченный по ширине) спектр,
то он может быть восстановлен однозначно
и без потерь по своим дискретным отсчётам,
взятым с частотой строго большей'
удвоенной верхней частоты ![]() :
:
![]()
x (t)→x(ti)
→x(k∆t)
(t)→x(ti)
→x(k∆t)
Теорема
Котельникова доказывает следующее:
 ,
где ∆t=1/(2fc)=1/(2πωc)
(Частота Котельникова, частота Найквиста)
,
где ∆t=1/(2fc)=1/(2πωc)
(Частота Котельникова, частота Найквиста)
Графическая интерпретация ряда Котельникова.
52. Спектр прямоугольного сиганала
Рассмотрим периодическую последовательность прямоугольных импульсов, изображенную на рис. 5. Данный сигнал характеризуется длительностью импульса, его амплитудой и периодом. По вертикальной оси откладывается напряжение.
 рис. 5
рис. 5
Начало отсчета выберем в середине импульса. Тогда сигнал разлагается только по косинусам. Частоты гармоник равны n/T , где n - любое целое число. Амплитуды гармоник согласно (1.2.) будут равны:

![]()
так
как V(t)=Е при  ,
где
,
где 
![]() -
длительности импульса и V(t)=0 при
-
длительности импульса и V(t)=0 при  ,
то
,
то

Эту формулу удобно записать в виде:
 (2.1.)
(2.1.)
Формула
(1.5.) дает зависимость амплитуды n-ой
гармоники от периода и длительности в
виде непрерывной функции (функция  ).
Эту функцию называют огибающей спектра.
Следует иметь ввиду, что физический
смысл она имеет только на частотах, где
существуют соответствующие гармоники.
На рис. 6 приведен спектр периодической
последовательности прямоугольных
импульсов.
).
Эту функцию называют огибающей спектра.
Следует иметь ввиду, что физический
смысл она имеет только на частотах, где
существуют соответствующие гармоники.
На рис. 6 приведен спектр периодической
последовательности прямоугольных
импульсов.

Рис.6. Спектр периодической последовательности
прямоугольных импульсов.
При
построении огибающей имеем ввиду,
что - является
является
осцилирующей
функцией частоты, а знаменатель монотонно
возрастает с ростом частоты. Поэтому
получается квазиосцилирующая функция
с постепенным убыванием. При частоте
стремящейся к нулю, к нулю стремятся
одновременно и числитель и знаменатель,
их отношение стремится к единице (первый
классический предел). Нулевые значения
огибающей возникают в точках где  т.
е.
т.
е.

, где m – целое число (кроме m=0). Переходя от циклической частоты к частоте в Гц, получаем:
 (2.2.)
(2.2.)
Эти значения отмечены на рис. 6.
Огибающая ограничивает на графике амплитуды гармоник. Форма огибающей определяется формой и длительностью импульса, а частоты гармоник только его периодом /2/. Это утверждение, полученное для прямоугольных импульсов справедливо и для других периодических сигналов.
Для того чтобы применить данные о периодическом сигнале к одиночному импульсу представим, что этот импульс повторяется с некоторым периодом Т и устремим этот период к бесконечности. Расстояние между соседними гармониками в спектре периодического сигнала равно 1/T . Следовательно, для T стремящегося к бесконечности расстояние между гармониками стремится к нулю, т. е. они сливаются. Амплитуды этих гармоник, стремятся к нулю, т. к. интеграл берется только в пределах существования импульса (вне импульса v(t)=0 ), а Т в знаменателе неограниченно возрастает.
Итак, отдельных гармоник в спектре одиночного импульса не будет. Этот спектр является сплошным (в него входят все частоты).
Очевидно, нулевые амплитуды гармоник не могут использоваться для описания спектра.
Для характеристики одиночных импульсов вводят новую характеристику: спектральную плотность S(f). Под спектральной плотностью понимают предел отношения амплитуды гармоник к расстоянию между соседними при Т стремящемся к бесконечности.
Удобно рассмотреть это на примере четного сигнала. Согласно определению:
 (4.1.)
(4.1.)
где Df=1/T- расстояние между соседними гармониками.
 (4.2.)
(4.2.)
Интегрировать достаточно в пределах до t/2 , так как дальше v(t)=0. Поэтому
 (4.3.
(4.3.
Видно, что выражение для S(w) и для огибающей В(w) отличаются только константой (периодом в знаменателе В(w)).
Зависимость спектральной плотности от частоты для одиночного импульса полностью повторяет форму огибающей Вi(w) для периодической последовательности таких же импульсов.
На рис. 8 приведены для примера спектры периодической последовательности прямоугольных импульсов и одиночного импульса:
Рис.8. Сравнение периодического и непериодического
сигналов и их спектров
Зависимость S(f) в отличие от Вi(w) изображается сплошной линией, а не пунктиром, так как S(f) существует во всех точках графика. Для импульса общего вида (не являющегося четным) следует вводить отдельно спектральную плотность для Sin и Cos в разложении Фурье или, что обычно и делается, применять метод комплексных амплитуд и рассматривать спектральную плотность в комплексном виде S`(w).
При использовании комплексной спектральной плотности S`(w) для одиночного импульса ряд Фурье переходит в преобразования Фурье:

 (4.4.)
(4.4.)
Формулы (4.4.) представляют прямую и обратную зависимость сигнала и его спектра. Интегрирование чаще всего производится в пределах существования сигнала. Например, импульс будет существовать (не быть равным нулю) только в течение его длительности.
