14. Измерение случайных процессов.

Измерить случ. процесс – определить его статистич. хар-ки, кот. определяются по одной или нескольким реализациям и эти хар-ки отражают с-ва всего процесса. Случ. процесс, набл. за короткий промежуток времени – наз. РЕАЛИЗАЦИЕЙ. Совокупность реализаций случайного процесса называется АНСАМБЛЕМ.

К хар-кам случ. процесса можно отнести среднее значение квадрата, мат. ожидание, дисперсию, среднеквадрат. отклонение, закон распределения:

1) Среднее значение квадрата:

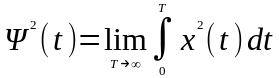
2) Математическое ожидание:

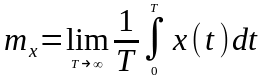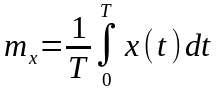, - среднее значение процесса.

3) Дисперсия

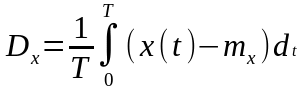
Математическое ожидание и дисперсия в дискретном виде:

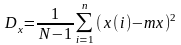
4) Функция распределения (и её вывод)

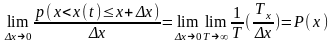- функция распределения

Если предел существует, то он назыв. функцией плотности распределения или одномер. законом распределения. Она обладает теми же свойствами:

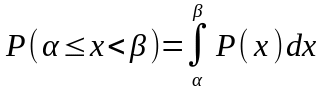
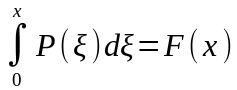, где F(x) – оригинал.

Все статистич. хар-тики получ. путём осреднения, при этом осреднение может осущ. осреднением по ансамблю либо осреднению по времени.

Случ. процесс обладает свойством ЭРГОДИЧНОСТИ, если статистич. характеристикики, найдены осреднением по времени и по ансамблю равны. Будем исходить из гипотезы эргодичности и осреднять будем по времени.

15. Числовые характеристики случайных процессов, их инженерно-физический смысл.

1) Среднее значение квадрата:

2) Мат. ожидание:

, - среднее значение процесса.

3) Дисперсия

Мат. ожидание и дисперсия в дискретном виде:

4) Функция распределения (и её вывод)

- ф-ция распределения

Если предел сущ., то он наз. функцией плотности распределения или одномер. законом распределения. Она обладает теми же свойствами:

- , где F(x) – оригинал.

Измерить случ. процесс – определить его статистич. характеристики, которые определяются по одной или нескольким реализациям и эти хар-ки отражают св-ва всего процесса. Случ. процесс, набл. за короткий промежуток времени – наз. РЕАЛИЗАЦИЕЙ. Совокупность реализаций случ. процесса наз. АНСАМБЛЕМ.

К хар-кам случ. процесса можно отнести среднее значение квадрата, мат. ожидание, дисперсию, среднеквадрат. отклонение, закон распред-я:

Все статистич. хар-тики получ. путём осреднения, при этом осреднение может осущ. осреднением по ансамблю либо осреднению по времени.

Случ. процесс обладает с-вом ЭРГОДИЧНОСТИ, если статистич. хар-ки, найдены осреднением по времени и по ансамблю равны. Будем исходить из гипотезы эргодичности и осреднять будем по времени.

16.Законы распределения и основные характеристики случайных процессов

Сечение с.п. X(t) при любом фиксированном значении аргумента t представляет собой случайную величину, которая имеет закон распределения

F(t,x) = P{X(t) < x} (1)

Эта функция зависит от двух аргументов: во-первых, от значения t, для которого берется сечение; во вторых, от значения х, меньше которого должна быть с.в. X(t) (Рис.4.). Функция (1) называется одномерным законом распределения.

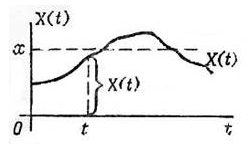
Рис.4.

Представим себе два случайных процесса с одинаковым распределением в каждом сечении, но совершенно различных по своей структуре. Первый представлен совокупностью своих реализаций на рис.5, второй – на рис.6. Первый процесс имеет плавный характер, второй – более резкий, «нервный». Для первого процесса характерна более тесная зависимость между сечениями с.п.; для второго эта зависимость затухает довольно быстро с увеличением расстояния между сечениями.

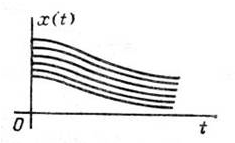
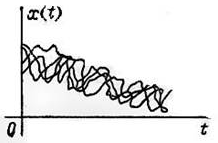
Рис.5.

Рис.6.

Очевидно, одномерный закон не может служить полной, исчерпывающей характеристикой с.п. X(t).

Одномерная функция распределения вероятностей F(x, t_i) определяет вероятность того, что в момент времени t_i значение случайной величины X(t_i) не превысит значения x:

F(x, t_i) = P{X(t_i)≤x}.

Очевидно, что в диапазоне значений вероятностей от 0 до 1 функция F(x, t) является неубывающей с предельными значениями F(-,t)=0 и F(,t)=1. При известной функции F(x,t) вероятность того, что значение X(ti) в выборках будет попадать в определенный интервал значений [a, b] определяется выражением:

P{a<X(t_i)≤b} = F(b, t_i) – F(a, t_i).