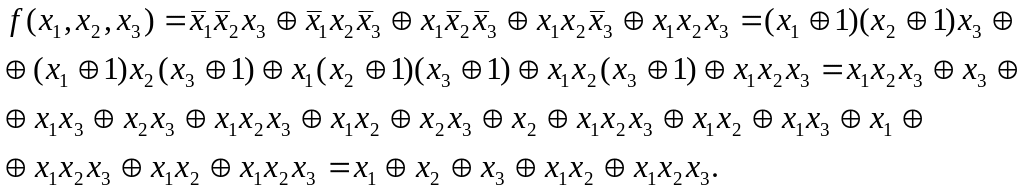3.5. Канонические формы аналитического представления пф
Конституентой единицы называется функция, принимающая значение 1 только на одном наборе переменных. Конституента единицы записывается как логическое произведение n различных переменных, некоторые из которых или все могут быть с отрицаниями.
Конституентой нуля называется функция, принимающая значение 0 на единственном наборе переменных. Конституента нуля записывается как логическая сумма n различных переменных, часть которых или все могут быть с отрицаниями.
Любую
конституенту 1 можно записать в виде
конъюнкции всех ее аргументов, при этом
переменная
записывается с инверсией, если в наборе,
на котором функция принимает значение
1, переменная
принимает значение 0. Например, логическое
произведение
соответствует конституенте 1, принимающей
единичное значение на наборе
,
,
.
На всех остальных наборах, как следует
из определения, конституента 1 принимает
значение 0. Вышеприведенное утверждение
может быть доказано, например, методом
перебора.
Каждому
i-му
набору аргументов
поставим в соответствие конституенту
единицы
,
принимающую единичное значение только
на этом наборе.
Любую переключательную функцию, зависящую от n аргументов, можно представить в виде разложения Шеннона:
.
Произведем разложение Шеннона по всем переменным:
В полученном выражении заменим наборы аргументов, представленных конъюнкциями переменных, на соответствующие конституенты 1. Тогда переключательная функция в общем виде может быть представлена следующим образом:
,
где
– значение функции на i-м
наборе.
Воспользовавшись
тем, что
и
,
в последнем выражении можно исключить
слагаемые, для которых
.
Учитывая, что
,
можно не писать коэффициенты
.
Таким
образом, искомую функцию
можно представить в виде дизъюнкции
конституент 1, соответствующих наборам
аргументов, на которых она принимает
значение 1. Такая форма записи называется
совершенной
дизъюнктивной нормальной формой
(СДНФ). Такое название объясняется тем,
что каждый дизъюнктивный член включает
в себя произведение всех n
аргументов (совершенная форма) и каждое
произведение является элементарным,
т.е. под знаком инверсии могут быть
только отдельные переменные (нормальная
форма).
В
качестве примера рассмотрим процедуру
записи СДНФ логической функции
,
заданной таблицей истинности (табл.
3.7). Для представления этой функции в
виде СДНФ необходимо выполнить следующие
действия, основанные на вышеприведенных
рассуждениях.
Таблица 3.7
|
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
|
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
|
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
|
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
На первом этапе запишем функцию в виде дизъюнкции конституент единицы, соответствующих тем наборам, на которых функция принимает значение 1:
Затем, выразив конституенты единицы через произведения аргументов, получим искомую СДНФ:
Из СДНФ функции и СДНФ ее отрицания, используя законы де Моргана, можно получить еще семь канонических форм.
Другой канонической формой записи является совершенная конъюнктивная нормальная форма (СКНФ). Ее отличие от СДНФ заключается в том, что СКНФ записывается как конъюнкция конституент нуля, соответствующих тем наборам, на которых функция принимает значение 0. При этом конституенты 0 записываются в виде элементарных дизъюнкций аргументов xi, инверсии которых соответствуют единичному значению аргумента.
Для примера запишем СКНФ функции, заданной табл. 3.7, при этом выполним последовательность действий, аналогичную той, которая была приведена в предыдущем примере.
На первом этапе запишем функцию в виде конъюнкции конституент нуля, соответствующих тем наборам, на которых функция принимает значение 0:
Далее, выразив конституенты нуля через дизъюнкции аргументов, получим искомую СКНФ:
С помощью законов де Моргана СКНФ функции можно получить из СДНФ ее отрицания, записываемой по нулям. В качестве примера рассмотрим преобразование отрицания СДНФ функции, заданной табл. 3.7:
откуда, избавляясь от операции отрицания в начальной и конечной частях выражения, получим
.
В СДНФ можно заменить операцию дизъюнкции операцией суммы по модулю 2. В том, что равенство при этом сохранится, можно убедиться путем сопоставления таблиц истинности получившихся выражений. Для рассмотренного выше примера:
Такая форма называется совершенной полиномиальной нормальной формой (СПНФ).
Воспользуемся
соотношением
и заменим в СПНФ все переменные с
отрицаниями на суммы вида
.
После упрощения полученного выражения
образуется канонический полином
Жегалкина, который в общем виде можно
записать следующим образом [4]:
Для рассматриваемого примера:
