5 Определение полосы частот

Прежде чем решать эту задачу, определим для себя понятие «Классическое частотное уплотнение». При таком способе уплотнения сигналы индивидуальных каналов можно записать в виде:

,

причем информация закладывается в изменения огибающей , фазы или одновременно в изменения обоих этих параметров. Здесь - средняя частота в спектре индивидуального сигнала. Эти частоты выбираются так, чтобы индивидуальные сигналы практически не перекрывались по спектру.

Решение задачи начнем с нахождения минимально необходимого разноса:

Учитывая защитный интервал находим разнос

, откуда ,

так как

Тогда занимаемая многоканальной системой полоса частот :

Оценим эффективность системы по критерию использования пропускной способности системы, в основе которого лежит отношение суммарной пропускной способности отдельных каналов системы к пропускной способности общего тракта

системы .

Находим численное значение эффективности системы:

Данный критерий характеризует использование полосы частот, отведенной для системы, и помехоустойчивость системы.

////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////

Завдання 2

Задано стаціонарний випадковий процес.

,

де Am,  - невипадкові величини, а  - випадкова фаза.

Знаходження середнього значення СВП полягає в обчисленні математичного очікування за формулою

, (2.1), (3)

де f(ф) – щільність розподілу випадкової фази .

Для величини, рівномірно розподіленої на проміжку [a, b], щільність імовірності дорівнює

.

В нашому випадку фаза рівномірно розподілена на проміжку [-, ], тому

.

Для нашої задачі інтеграл (2.1) приймає вигляд:

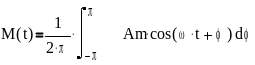, (2.2)

розв’яжемо його.

,

.

Кореляційна функція в загальному випадку обчислюється за формулою:

. (2.3), (3)

Як було визначено вище, математичне очікування даного СВП дорівнює нулю, тобто формула (2.3) набуває вигляд:

. (2.4)

Знайдемо кореляційну функцію заданого СВП.

,

,

,

.

Дисперсія є ні що інше як кореляційна функція в нулі:

.

Завдання 3

Якщо кількість інформації в прийнятому повідомленні дорівнює I, а загальна тривалість повідомлення дорівнює Т, то швидкість передачі

V=I/T біт/с. (3.1), (1)

Максимально можлива швидкість передачі інформації по каналу зв’язку при фіксованих обмеженнях називається пропускною здатністю канала зв’язку:

C=maxV. (3.2), (1)

У випадку неперервного каналу визначення С зводиться до максимізації І при заданих фіксованих обмеженнях.

Кількість інформації, яка міститься в прийнятій сукупності повідомлень Y відносно переданої X, представляє собою різницю між ентропією джерела та втратами:

I(Y, X)=H(X)-H(X/Y). (3.3), (1)

Повідомлення та завади повністю статистично незалежні, тому умовна ентропія H(X/Y) є додатковою ентропією, яку дає знання повідомлень Y. Вона обумовлена лише завадами, тому

H(X/Y)=H(N), (3.4), (1)

де H(N) – ентропія завад.

Таким чином можемо переписати (3.3) згідно з (3.4) наступним чином:

I(Y, X)=H(Y)-H(N). (3.5), (1)

Нехай тривалість повідомлення дорівнює Т_с, а передані повідомлення x(t), завади n(t), прийняті повідомлення y(t) мають обмежений частотний спектр з верхньою граничною частотою F_в. Згідно з теоремою Котєльнікова, згідно з якою розіб’ємо інтервал часу Т_с на рівні відрізки величиною t=1/(2F_в). Перепишемо (3.5) наступним чином:

H(N)=2F_вT_cH(n), (3.6), (1)

де H(n) – ентропія завад для одного відлікового значення. Якщо перешкода розподілена за нормальним законом, то (3.6) приймає вигляд:

H(n)=log-logx. (3.7), (1)

Підставимо (3.7) в (3.6):

H(N)=2F_вT_c(log-logx). (3.8), (1)

Якщо вважати, що відлікові значення прийнятого повідомлення y(t) статистично незалежними, то ентропія

H(Y)=2F_вT_c(H(y)-logy). (3.9), (1)

Вважаємо, що величини x та y однакові, тобто:

I(Y,X)=2F_вT_c(log-log). (3.10), (1)

Потужність прийнятого сигналу можна розписати у вигляді:

P_y=P_c+P_n. (3.11), (1)

Підставимо значення Ру в (3.10), отримаємо:

I(Y,X)=2F_вT_clog, (3.12), (1)

I(Y,X)=2F_вT_clog(1+ ). (3.13), (1)

За умовою задачі перешкода розподілена за рівномірним законом, тому необхідно використовувати ентропійну потужність:

P_ент(n)= , (3.14), (1)

Для рівномірного закону, який діє на проміжку [a; b], ентропія дорівнює

. (3.15), (1)

З теорії імовірностей відомо, що середнє квадратичне відхилення для рівномірного закону дорівнює:

_п= . (3.16), (3)

Тобто ми можемо зробити заміну

b-a=_п. (3.17)

P_ент(n)= , (3.18)

P_ент(n)= . (3.19)

Пам’ятаємо, що квадрат середнього квадратичного відхилення є дисперсією, яка в свою чергу дорівнює потужності, тобто (3.19) приймає вигляд:

P_ент(n)= . (3.20)

Оціночне значення ентропійної потужності

P_oент(n)= . (3.21)

Якщо підставити в (3.13) замість Рn Рент(n) з (3.20), та Роент з (3.21), то отримаємо значення кількості інформації, причому Іо(Y,X) – оціночне значення кількості інформації.

I(Y,X)=F_вT_clog. (3.22)

I₀(Y,X)=F_вT_clog. (3.23)

Отримане значення I(Y,X) визначає максимальну кількість інформації, яка може міститися в повідомленнях Y відносно X.

З формул (3.1), (3.2) та (3.22) пропускна здатність дорівнює

C=F_вlog. (3.24)

Формулу оціночного значення пропускної здатності отримаємо з (3.1), (3.2) та (3.23):

C₀=F_вlog. (3.25)

Обчислимо оціночне значення пропускної здатності за формулою (3.25), підставляючи задані значення Рс=1 Вт, Рn=0,001 Вт, Fв=10⁴ Гц,

Со1,048 ^. 10⁵ біт/с.

Підставимо в (3.24) задані параметри: Рс=1 Вт, Рn=0,001 Вт, Fв=10⁴ Гц, отримаємо числове значення пропускної здатності:

С1,33 ^. 10⁵ біт/с.

////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////

4. Одержана кодова комбінація циклічного коду x⁶ + x⁴ + x² + 1. В каналі використаний циклічний код із сворюючим поліномом Р(х)= x³ + x + 1.Чи були помилки при передачі ? Визничити місце одиничної помилки .

Маємо комбинацию циклічного коду

A_y(x)=x⁶+x⁴+x²+1

створюючий поліномом

a(x)=х³+х+1

Перевіримо чибули помилки при перелаачі , для цього поділимо А_у(х) на G(x) та проаналізуємо залишок :

х⁶+х⁴+х²+1 х³+х+1

х⁶+х⁴+х³

х³+1

х³+х²+1

х³+ х +1

х²+х

Отже R(x)=x²+x =0 робимо висновок ,що помилки мали місце під час передачі :

Підберемо такий поліном А_у , щоб при діленні на G(t) R(x)=0.

Спрбуємо А_у =х⁶+х²+1

х⁶+х²+1 х³+х+1

х⁶+х⁴+х³

х³+х+1

х⁴+х³+х²+1

х⁴+х²+х

х³+х+1

х³+х+1

0

R(x)=0 , отже правильною комбінацією є А_у(х)=х⁶+х²+1 , і одиночна помилка була у 5 .

1010101 – прийнята комбінація

1000101 -- правильна комбінаці

////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////