ВСТУП 4

1. ІНТЕРПОЛЯЦІЯ 4

1.1. Наближення функцій. Задача інтерполяції 4

1.2 Інтерполяційний багаточлен Лагранжа 7

1.3 Похибка інтерполяції багаточленом 9

1.4.Інтерполяція з рівновіддаленими вузлами 10

1.5.Скінчені та поділені різниці 13

1.6.Інтерполяційний багаточлен Ньютона 18

1.7 Інтерполювання сплайнами 22

2 ЧИСЛОВЕ ДИФЕРЕНЦІЮВАННЯ 26

3 ЧИСЛОВЕ ІНТЕГРУВАННЯ 31

3.1 Квадратнурні формули 32

3.2 Формула прямокутників 32

3.3 Формула трапецій 34

3.4.Формула Сімпсона 37

3.5 Ускладнені квадратурні формули 39

4 ЗАВДАННЯ ДО РОЗРАХУНКОВОЇ РОБОТИ 43

Завдання 1 43

Завдання 2 44

СПИСОК ЛІТЕРАТУРИ 45

ВСТУП

Методичні вказівки являються продовженням методичних вказівок «Методи розв’язання систем лінійних алгебричних і нелінійних рівнянь та їх систем. Проблема власних значень » і містять нові розділи теоретичного курсу і практичні завдання для виконання розрахункової роботи, а саме: задачі інтерполяції, числове диференціювання та інтегрування. Враховуючи стислість одно-семестрового курсу, автори відібрали тільки класичні методи числового розв’язання відповідних математичних задач з прозорою алгоритмічною структурою, математичне обґрунтування яких не перевантажене складними логічними побудовами та громіздкими викладками. Також радимо ознайомитись з іншими методами розв’язання задач за наведеною літературою. Методи розв’язання залежно від ситуації можуть дати ефективніші алгоритми з точки зору точності та кількості арифметичних операцій та реалізації.

1. Інтерполяція

1.1. Наближення функцій. Задача інтерполяції

Задача наближення функцій виникає при розв’язанні багатьох задач (обробка експериментальних даних, числове диференціювання та інтегрування функцій, розв’язання диференціальних та інтегральних рівнянь).

Дуже зручною у використанні на практиці функцією є багаточлен. Щоб задати багаточлен, треба задати тільки скінчену кількість його коефіцієнтів. Значення багаточлена просто обчислюються (згадаємо схему Горнера), його легко продиференціювати, проінтегрувати і т.і. Тому алгебраїчні багаточлени знайшли широке застосування для наближення (апроксимації) функцій.

Розглянемо декілька задач наближення функцій.

Постановка задачі інтерполяції. Нехай відомі значення деякої функції у різних точках які позначимо Виникає задача поновлення (наближеного) функції у довільній точці .

Іноді відомо, що наближену функцію доцільно шукати у вигляді

де вигляд функції відомий, а параметри треба визначити.

Коли параметри визначаються з умови збігу і наближеної функції у точках тобто то такий спосіб наближення називається інтерполяцією. Точки називаються вузлами інтерполяції.

Серед способів інтерполяції найбільш поширеним є випадок лінійної інтерполяції:

де - деякі відомі функції. Значення коефіцієнтів визначаються з умови збігу з вихідною функцією у вузлах інтерполяції

(1.1)

тобто з системи n +1 лінійних рівнянь з n+1 невідомими

У окремому випадку, коли

(1.2)

тобто інтерполяція здійснюється багаточленом, який називається інтерполяційним.

ТЕОРЕМА 1.1. Якщо вузли інтерполяції різні, то існує єдиний інтерполяційний багаточлен -го ступеня.

Доведення . Дійсно, система рівнянь (1.1) у цьому випадку має вигляд

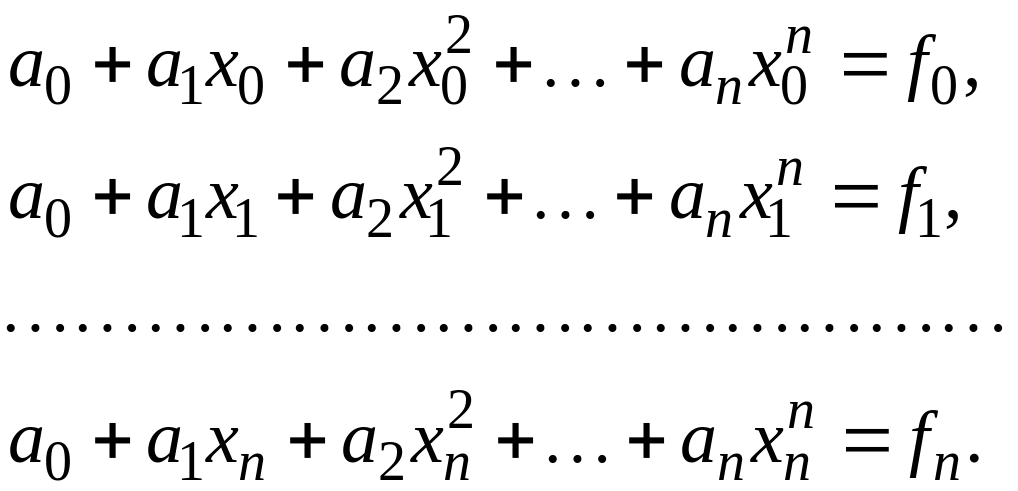(1.3)

Її визначник є визначником Вандермонда

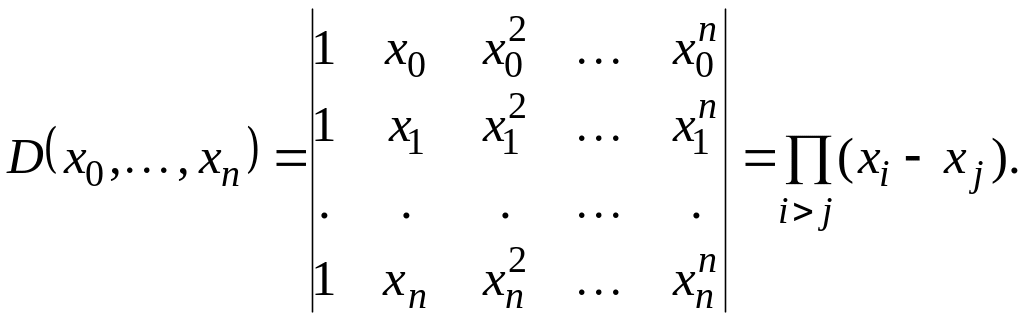(1.4)

У тому, що має місце права частина рівності (1.4) , можна переконатися наступним чином. Віднімаючи перший рядок з усіх наступних, маємо

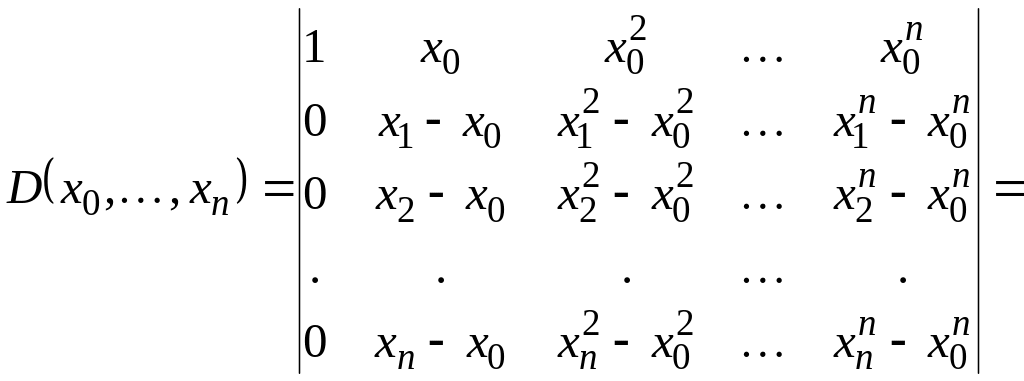
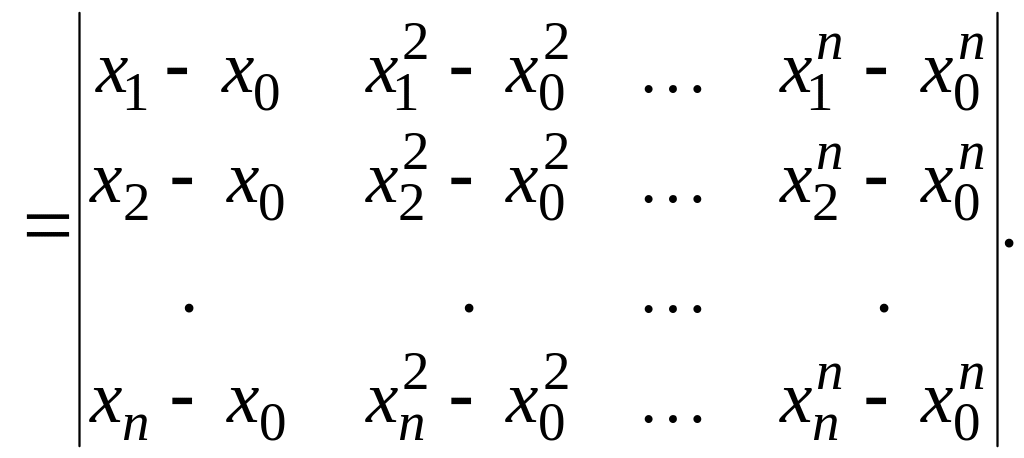
Віднімаючи тепер з кожного стовпця попередній, що множиться на одержимо

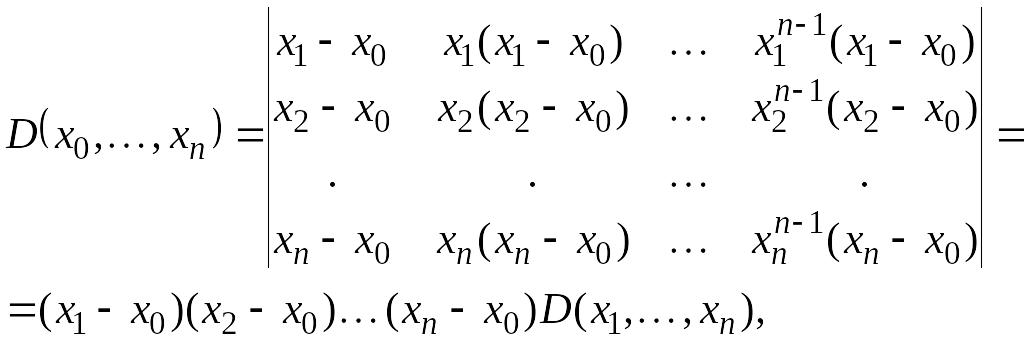
де

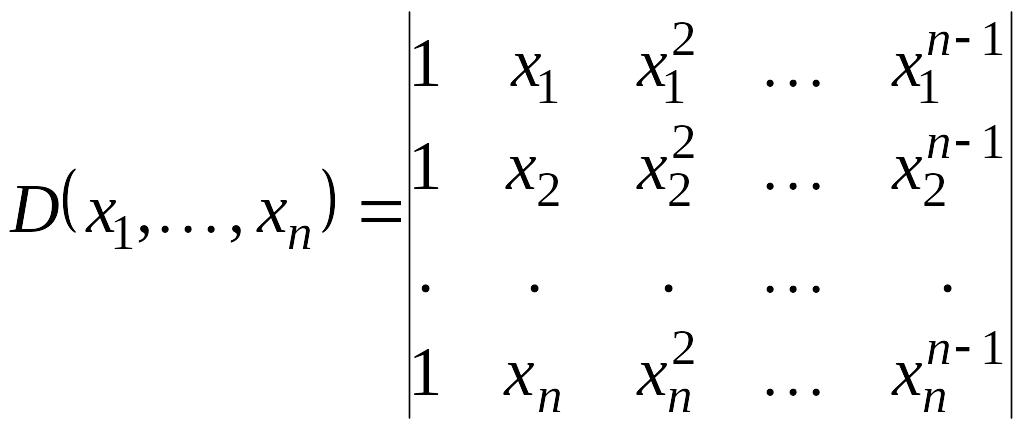
теж є визначником Вандермонда, порядок якого на одиницю менше порядку попереднього.

Зробивши з ним те ж, що з попереднім, одержимо

Продовжуючи аналогічні викладки, остаточно одержимо рівність (1.4). Бачимо, що при Тобто система (1.3) має єдиний розв’язок. Теорема доведена.

Таким чином, інтерполяційний поліном можна одержати шляхом розв’язання системи лінійних алгебраїчних рівнянь (1.3).

1.2 Інтерполяційний багаточлен Лагранжа

Інтерполяційний багаточлен може бути записаний не тільки у формі (1.2). Існують і інші форми зображення інтерполяційного багаточлена, які можна записати відразу через вихідні дані задачі, тобто через не розв’язуючи систему (1.3).

ТЕОРЕМА 1.2. Інтерполяційний багаточлен може бути записаний у формі

(1.5)

яка називається інтерполяційним багаточленом Лагранжа.

Доведення. Переконаємось у цьому безпосередньо.

При маємо

(1.6)

Бачимо, що вираз (1.6) є багаточленом першого ступеню, причому підстановкою переконуємося , що

При

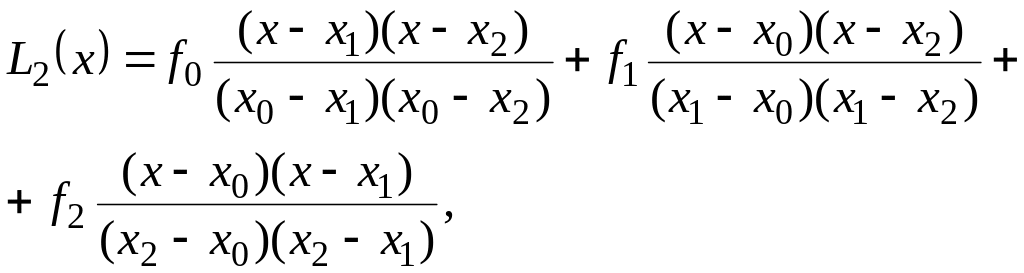
тобто маємо багаточлен другого ступеню і

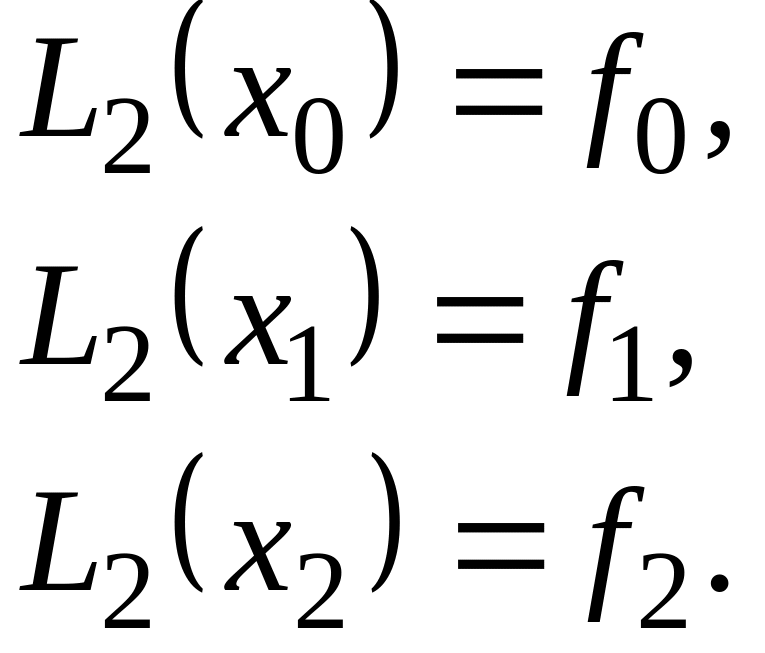
Нарешті, для довільного натурального

(1.7)

де

(1.8)

Функції (1.8) є багаточленами ступеню . Отже (1.7) теж є алгебраїчним багаточленом ступеню . Оскільки при маємо

Функції (багаточлени ) (1.8) називаються лагранжевими коефіцієнтами .

Зауважимо, що оскільки інтерполяційний багаточлен (1.7) лінійно залежить від значень функції то інтерполяційний багаточлен суми двох функцій дорівнює сумі інтерполяційних багаточленів доданків (коли вузли інтерполяції співпадають).