
- •1. Інтерполяція
- •1.1. Наближення функцій. Задача інтерполяції
- •1.2 Інтерполяційний багаточлен Лагранжа
- •1.3 Похибка інтерполяції багаточленом
- •1.4.Інтерполяція з рівновіддаленими вузлами
- •1.5.Скінчені та поділені різниці
- •1.6.Інтерполяційний багаточлен Ньютона
- •1.7 Інтерполювання сплайнами
- •2 Числове диференціювання
- •3 Числове інтегрування
- •3.1 Квадратнурні формули
- •3.2 Формула прямокутників
- •3.3 Формула трапецій
- •3.4.Формула Сімпсона
- •3.5 Ускладнені квадратурні формули
- •4 Завдання до розрахункової роботи
- •Завдання 1
- •Завдання 2
- •Список літератури
1.5.Скінчені та поділені різниці
Скінчені різниці.
Нехай
![]() де
де
![]() - ціле,
- ціле,
![]()
![]() .
.
Величина
![]() (1.17)
(1.17)
називається скінченою
різницею першого порядку
функції
у точці
![]() (з кроком
).
(з кроком
).
Величина
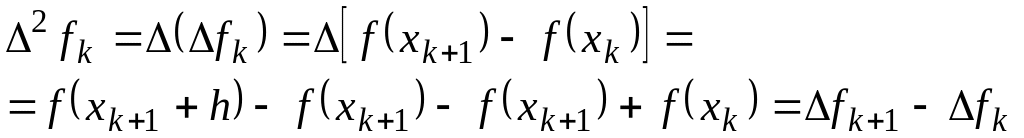 (1.18)
(1.18)
називається скінченою різницею другого порядку функції у точці .
Взагалі, скінчена різниця
-го
порядку функції
у точці
![]() визначається рекурентним співвідношенням
визначається рекурентним співвідношенням
![]() (1.19)
(1.19)
де
![]() .
.
При обчисленнях скінченні різниці зручно записувати у вигляді таблиці

Розглянемо деякі властивості скінчених різниць.
Лема 1.1.
Якщо
![]() ,
то існує така точка
,
то існує така точка
![]() ,
що
,
що
![]() .
.
Доведення. При маємо з формули скінчених приростів Лагранжа та з (1.17)
![]()
При
![]() маємо. Позначимо
маємо. Позначимо
![]() Тоді згідно (1.18)
Тоді згідно (1.18)
![]()
і тому за формулою скінчених приростів Лагранжа
![]() (1.20)
(1.20)
Але
![]() .
.
Застосовуючи ще раз формулу
скінчених приростів Лагранжа до
![]() ,
маємо
,
маємо
![]() (1.21)
(1.21)
де
![]() деяка точка.
деяка точка.
З формул (1.20), (1.21) виходить
![]() тобто твердження леми при
справедливо.
тобто твердження леми при
справедливо.
Для
![]() лема доводиться аналогічно.
лема доводиться аналогічно.
Висновок з леми 1.1. Скінчена різниця -го порядку алгебраїчного багаточлена -го ступеню стала, тобто не залежить від , а скінченні різниці ще вищих порядків дорівнюють нулеві.
Одне з практичних застосувань
скінчених різниць полягає у наступному.
Згідно леми 1.1, якщо
![]() , то величина
, то величина
![]() яку можна обчислити через табличні
значення функції
за допомогою формули (1.19), дорівнює
значенню похідної
яку можна обчислити через табличні
значення функції
за допомогою формули (1.19), дорівнює
значенню похідної
![]() у деякій точці
у деякій точці
![]() ,
де
,
де
![]()
Тому , якщо
мале, то число
![]() можна наближено прийняти за величину
можна наближено прийняти за величину
![]() та використати в оцінці похибки
інтерполяції з рівновіддаленими вузлами.
Такою нестрогою оцінкою похибки
користуються, якщо достатньо складне
обчислення похідної
та використати в оцінці похибки
інтерполяції з рівновіддаленими вузлами.
Такою нестрогою оцінкою похибки
користуються, якщо достатньо складне
обчислення похідної
![]() ,
або, взагалі, маємо у розпорядженні
тільки табличні значення
раз диференційованої функції.
,
або, взагалі, маємо у розпорядженні
тільки табличні значення
раз диференційованої функції.
Поділені різниці.
Нехай тепер
![]() -
довільні точки (вузли) осі
,
причому
-
довільні точки (вузли) осі
,
причому
![]() при
при
![]() .
.
Значення
![]() функції
у вузлах називаються поділеними
різницями нульового порядку.
функції
у вузлах називаються поділеними
різницями нульового порядку.
Число
![]() (1.22)
(1.22)
називається поділеною
різницею першого порядку функції
(відповідно точкам
![]() ).
).
Очевидно
![]() (1.23)
(1.23)
тобто поділена різниця першого
порядку є симетричною функцією аргументів
![]() і
і
![]() .
.
Поділена різниця
-го
порядку визначається через поділені
різниці
![]() -го
порядку за рекурентною формулою
-го
порядку за рекурентною формулою
![]() (1.24)
(1.24)
При обчисленнях поділені різниці записують у вигляді таблиці

Лема 1.2. Поділена різниця -го порядку може бути подана через вузлові значення функції за формулою
 (1.25)
(1.25)
тобто є симетричною функцією своїх аргументів .
Доведення . При твердження леми виходить з рівності (1.23).
При згідно з (1.24) маємо

Для довільного доведення проводиться за індукцією.
Висновок з леми 1.2.
Значення поділеної різниці не залежить
від порядку нумерації
![]() вузлів, за якими вона будується. Всього
маємо
вузлів, за якими вона будується. Всього
маємо
![]() варіантів нумерації вузлів цілими
числами від 0 до
.
варіантів нумерації вузлів цілими
числами від 0 до
.
Лема 1.3.
Якщо
![]() тобто вузли розміщуються на осі з сталим
кроком
тобто вузли розміщуються на осі з сталим
кроком
![]() то між поділеною різницею
-го
порядку та скінченою різницею
-го
порядку існує наступний зв’язок:
то між поділеною різницею
-го
порядку та скінченою різницею
-го
порядку існує наступний зв’язок:
![]() . (1.26)
. (1.26)
Доведення.
Для
=1
рівність (1.26) виходить з (1.17), (1.23). При
довільному
доведення проводиться за індукцією.
При цьому враховується той факт, що при
визначенні кожної наступної за порядком
скінченої різниці відбувається згідно
(1.19) віднімання попередніх різниць, а
при обчисленні наступної поділеної
різниці згідно з формулою (1.24) проводиться
додаткове ділення на величину
![]() Звідси й виникає величина
Звідси й виникає величина
![]() у
знаменнику правої частини рівності
(1.26).
у
знаменнику правої частини рівності
(1.26).
Лема 1.4.
Нехай
![]() - мінімальний відрізок, що містить вузли
- мінімальний відрізок, що містить вузли
![]()
![]() .
Тоді існує така точка
.
Тоді існує така точка
![]() що
що
![]() .
(1.27)
.
(1.27)
Доведення . Для вузлів, що розміщені зі сталим кроком, рівність (1.27) безпосередньо виходить з лем 1.1, 1.3.
Доведення у загальному випадку
можна здійснити наступним чином. Візьмемо
точку
![]()
![]()
![]() та побудуємо поділену різницю
-го
порядку
та побудуємо поділену різницю
-го
порядку

З цього виразу можна одержати

Співставимо останнє рівняння
з раніш одержаним виразом для похибки
![]() та одержимо
та одержимо
![]()
Покладаючи тепер
![]() ,
одержимо (1.27).
,
одержимо (1.27).
Висновок з леми 1.4. Поділена різниця -го порядку від алгебраїчного багаточлена -го ступеню має стале значення, що не залежить від вузлів а поділені різниці ще вищих порядків дорівнюють нулеві.
Скінченні і поділені різниці мають різноманітні застосування. Далі розглянемо їх використання для побудови інтерполяційних багаточленів.
