1.7 Інтерполювання сплайнами

Інтерполювання багаточленом Лагранжа або Ньютона на відрізку з використанням більшого числа вузлів інтерполяції часто призводить до поганого наближення , що пояснюється сильним накопиченням похибки в процесі обчислення. Крім цього через розходження процесу інтерполяції збільшення кількості вузлів не повинно приводити до підвищення точності .Для того , щоб обминути великої похибки , весь відрізок розбивають на окремі відрізки та на кожному з окремих відрізків приблизно замінюють функцію багаточленом невисокого ступеню (так звана кусково – поліноміальна інтерполяція).

Одним з способів інтерполяції на всьому відрізку являється інтерполювання за допомогою сплайн – функціями. Сплайн – функцією або сплайном називають кусково – поліноміальну функцію , яка визначена на відрізку та має на цьому відрізку деяке число неперервних похідних.

Слово “сплайн“ (англійське spline) означає гнучка лінійка, яка використовується для проведення гладких кривих через задані точки площини.

Перевага сплайнів перед звичайною інтерполяцією полягає, по – перше , у їх збіжності, і , по – друге, у сталості процесу обчислення.

Розглянемо частковий, але розповсюджений в обчислювальній практиці випадок, коли сплайн визначається за допомогою багаточленів третього ступеню (кубічний сплайн) .

Нехай задана неперервна функція . Введемо вузли (сітку):

та позначимо

Інтерполяційний кубічний сплайн , який відповідає даній функції , задовольняє наступні умови:

а) на кожному сегменті функція являється багаточленом третього ступеню;

б) функція , а також її перша та друга похідні неперервні на відрізку ;

в)

Остання умова називається умовою інтерполювання.

Доведемо існування та єдиність сплайна, який визначається вказаними умовами (плюс деякі граничні умови, які будуть введені в процесі побудови сплайна).

Побудова сплайна

На кожному з відрізків будемо шукати функцію у вигляді багаточлена третього ступеню

(1.32)

де - коефіцієнти, які підлягають визначенню. Знайдемо зміст введених коефіцієнтів. Маємо

тому

З умови інтерполювання отримуємо, що

Далі довизначимо , крім того, . З умови неперервності маємо

Звідси, враховуючи вираз для функції отримуємо при рівняння

Позначимо перепишемо рівняння у вигляді

(1.33)

Умова неперервності першої похідної

приводить до рівняння

(1.34)

З умови неперервності другої похідної отримуємо рівняння

. (1.35)

Об’єднуючи (1.33) ‑ (1.35), отримуємо систему рівнянь відносно невідомих

Дві умови, яких не вистачає, отримують, задаючи ті або інші граничні умови для Будемо вважати, що функція задовольняє умовам Тоді можна вимагати, щоб Звідси отримуємо тобто

Зауважимо , що умова співпадає з рівнянням (1.35) при .Таким чином , приходимо до замкнутої системи рівнянь для визначених коефіцієнтів кубічного сплайна:

(1.36)

(1.37)

(1.38)

Впевнимося у тому, що система має єдиний розв’язок. Виключимо з (1.36)‑(1.38) змінні та отримаємо систему, яка містить тільки Для цього розглянемо два сусідніх рівняння(1.38):

та віднімемо друге рівняння з першого. Тоді отримаємо

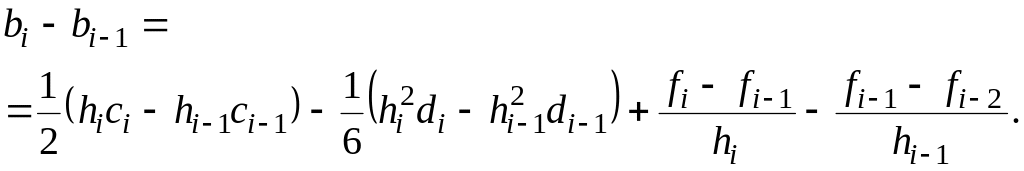
Підставимо знайдений вираз для в праву частину рівняння (1.37), отримаємо

(1.39)

Далі, з рівняння (1.36) отримуємо

Підставляючи ці вирази в (1.39) , приходимо до рівняння

Остаточно для визначення коефіцієнтів отримуємо систему рівнянь

(1.40)

В силу діагонального виду система (1.40) має єдиний розв’язок. Оскільки матриця системи трьох-діагональна, розв’язок можна знайти методом прогонки. По знайденим коефіцієнтам коефіцієнти і визначаються за допомогою явних формул

(1.41)

Таким чином, доведено, що існує єдиний кубічний сплайн, який визначається умовами а) і в) та граничними умовами

Зауважимо, що можна розглядати й інші граничні умови.