Билет № 10

1. Теорема о средней линии трапеции.

2. Формулы площади треугольника. Запись, вывод одной из них.

Вопрос № 1 Теорема о средней линии трапеции

Трапецией называется четырёхугольник, у которого две стороны парал­лельны, а две другие стороны не параллельны. Параллельные стороны трапе­ции называются её основаниями, а непараллельные стороны - боковыми сто­ронами.

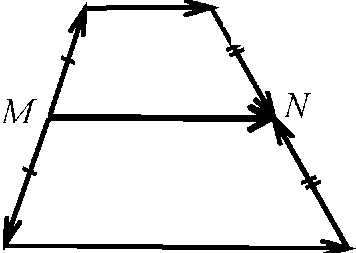
На рисунке ABCD - трапеция, ВС || AD, ВС и AD - основания, АВ Ц CD, АВ и CD - боковые стороны.

Средней линией трапеции называется отрезок, соединяющий середины её боковых сторон. На рисунке MN - средняя линия трапеции ABCD, так как АМ = МВ, CN = ND.

Теорема. Средняя линия трапеции параллельна основаниям и равна их полусумме.

B C

Дано: ABCD - трапеция, ВС || AD, MN - средняя линия.

Доказать: MN || ВС, MN || AD, MN = 2 (BC + AD).

A

Доказательство

По правилу многоугольника сложения нескольких векторов

MN = MB + BC + CN и MN = MA + AD + DN. Сложив эти равенства, получим

2mN = (MB+MA)+ (BC + ~AD)+ (CN + DN ).

По условию теоремы MN - средняя линия трапеции, поэтому M и N - се­редины сторон АВ и CD, а MB и MA, CNиDN - противоположные векторы. Так как сумма противоположных векторов равна нулевому вектору, то MB + MA = 0 и CN + DN = 0. Следовательно, 2MN = BC + AD, отсюда MN =¹ (BC + AD).

Так как BC tt AD , то MN tt BC и MN tt AD, а длина вектора BC + AD равна BC + AD. Отсюда следует, что MN || ВС, MN || AD и MN =¹ (BC + AD).

Итак, средняя линия трапеции параллельна основаниям и равна их полу­сумме.

Ч.т.д.

Вопрос № 2

Формулы площади треугольника. Запись, вывод одной из них

Одну из сторон треугольника часто называют его основанием. Если осно­вание выбрано, то под словом «высота» подразумевают высоту треугольника, проведенную к основанию.

Теорема. Площадь треугольника равна половине произведения его осно­вания на высоту.

a

Рис. 1 C D

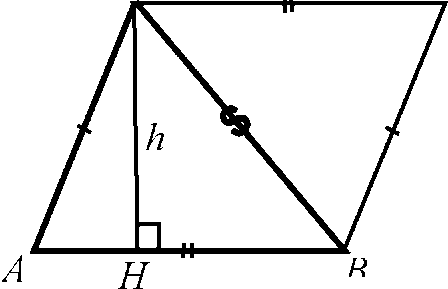
Дано: D АВС, АВ = а, СН = h.

Доказать: S_DАВС = 2ah.

Доказательство

Достроим треугольник АВС до параллелограмма ABDC так, как показано на рисунке 1. Рассмотрим треугольники АВС и DCB.

АС = BD и АВ = CD как противолежащие стороны параллелограмма, ВС - общая сторона. Следовательно, D АВС = D DCB по III признаку равенства тре­угольников (по трем сторонам).

Равные фигуры имеют равные площади, поэтому S_{D АВС} = S_D г>_СВ. По свойству площадей площадь параллелограмма равна сумме площадей тре­угольников, из которых он составлен, поэтому S^^ = S_{D АВС} + S_D г>_СВ = 2 S_{D АВС}. Значит, площадь D АВС равна половине площади параллелограмма ABDC.

Площадь параллелограмма ABDC равна произведению его основания а на

^высоту ^h, С^ДОШШ^НО, ^Sd ^ = 2 ^ah.

Итак, площадь треугольника равна половине произведения его основа­ния на высоту.

Ч.т.д.

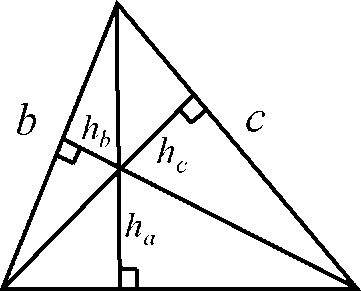
S_A = ¹ aha =¹ bhb = ¹ ch_c 2 2 2

a

Площадь прямоугольного треугольника

Sa

b

Площадь прямоугольного треугольника равна половине произведения его катетов.

1. ab

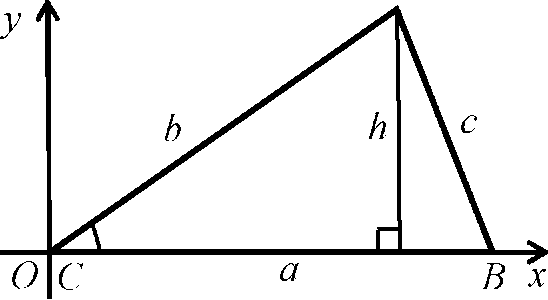
2. A(bcosC;b sinC )

Теорема. Площадь треугольника равна половине произведения двух его сторон на синус угла между ними.

Дано: А АВС, ВС = а, АС = b.

Доказать: S = —ab sin C.

Доказательство

Введем прямоугольную систему координат так, чтобы точка С совпала с началом координат, точка В лежала на положительной полуоси Ох, а точка А имела положительную ординату, тогда вершины треугольника будут иметь ко­ординаты С (0; 0), В (а; 0), A(bcosC; bsinC).

Площадь данного треугольника можно вычислить по формуле S = — ah, где h - высота треугольника. Но h равна ординате точки А, т.е. h = b sin C. Сле­довательно, S = ¹ ab sin C.

2

Итак, площадь треугольника равна половине произведения двух его сто­рон на синус угла между ними.

Ч.т.д.

Формула Герона

^S = V p ⁽p ^{- a} Xp -^{b )(}p -^c)^,

где а, b, с - стороны треугольника,

р - полупериметр треугольника,

Р = 2 ^(а + ^b + ^с).

a

Площадь равностороннего треугольника

S

где а - сторона треугольника.