Доказательство

Если ^ 1 и ^ 2 - прямые (рис. 1, б), то а ± АВ и b ± АВ, следовательно, а || b, так как две прямые, перпендикулярные третьей прямой, параллельны. Рассмотрим случай, когда ^ 1 и ^ 2 не прямые (рис. 1, а). Выполним дополнительные построения. Из точки О - середины отрезка АВ, проведём отрезок ОН L а. На прямой b от точки В отложим отрезок ВН₁ = АН, проведём отрезок ОН1 к прямой b.

Рассмотрим D ОНА и D ОН₁В. АО = ОВ, АН = ВН₁ по построению; ^ 1 = Z 2 по условию теоремы. Следовательно, D ОНА = D ОН₁В по I признаку равенства треугольников (по двум сторонам и углу между ними).

В равных треугольниках соответствующие элементы равны, поэтому ^ 3 = Z 4 и ^ 5 = Z 6. Так как ^ 3 = Z 4, то точка Н₁ лежит на продолжении луча ОН, то есть точки Н, О и Н₁ лежат на одной прямой. Так как ^ 5 = Z 6, то ^ 6 - прямой, потому что ^ 5 - прямой по построению.

Получили, что а ± НН₁ и b ± НН₁, следовательно, а || b, так как две пря­мые перпендикулярные третьей параллельны.

Итак, если при пересечении двух прямых секущей накрест лежащие уг­лы равны, то прямые параллельны.

Ч.т.д.

Теорема. Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.

Рис. 2

п

a Дано: прямые а и b, с - секущая,

^ 1 и ^ 2 - соответственные углы, ^ 1 = Z2 (рис. 2). b л' Доказать, а || b.

Доказательство

Z1 = Z2 по условию; ^ 2 = Z 3, так как они вертикальные. По свойству транзитивности ^ 1 = Z 3. Но ^ 1 и ^ 3 - накрест лежащие углы, поэтому по доказанному выше признаку а || b.

Итак, если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.

Ч.т.д.

Теорема. Если при пересечении двух прямых секущей сумма односто­ронних углов равна 180^о, то прямые параллельны.

Дано: прямые а и b, с - секущая,

^ 1 и ^ 4 - односторонние углы, ^ 1 + Z4 = 180^о (рис. 2).

Доказать: а || b.

Доказательство

^ 1 + Z 4 = 180^о по условию, отсюда

Z1 = 180^о - Z4. (1)

^ 3 + Z 4 = 180^о, т.к. ^ 3 и ^ 4 - смежные, отсюда

^ 3 = 180^о - ^ 4. (2)

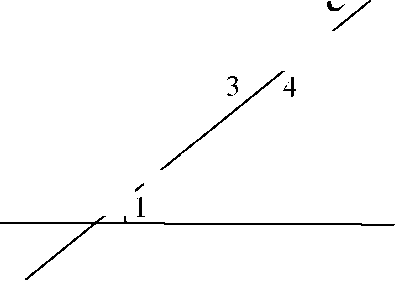
Правые части равенств (1) и (2) равны, поэтому равны и левые части. Следовательно, Z1 = Z 3. Но ^ 1 и ^ 3 - накрест лежащие, поэтому по дока­занному выше признаку а || b.

Вопрос № 2

Окружность. Определение, взаимное расположение прямой и окружности

Окружностью называется геометрическая фигура, состоящая из всех то­чек плоскости, расположенных на заданном (одинаковом) расстоянии от дан­ной точки.

Данная точка называется центром окружности, а отрезок, соединяющий центром с какой-либо точкой окружности, - радиусом окружности (рис. 1). Все радиусы имеют одну и туже длину.

Отрезок, соединяющий две точки окружности, называется хордой. Хорда, проходящая через центр окружности, называется диаметром. На рисунке 2 от­резки АВ, DE, EC, MN - хорды окружности, отрезок АВ - диаметр окружности.

Рис. 1

N Рис. 2

L

Рис. 3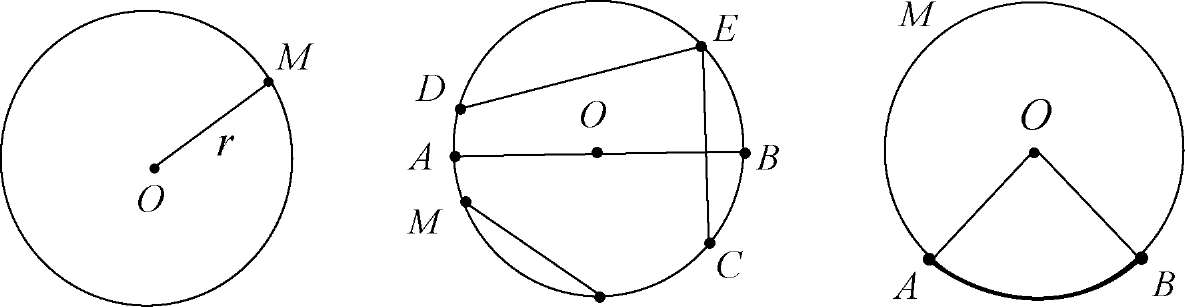

Диаметр - самая большая хорда, любой диаметр - хорда, но не всякая хорда является диаметром.

Диаметр в два раза больше ее радиуса. Центр окружности является сере­диной любого диаметра.

Если на окружности отметить две точки, то они разделят её на две части, каждая из которых называется дугой, то есть дуга - часть окружности, распо­ложенная между двумя точками этой окружности.

Чтобы различать эти дуги, на каждой из них отмечают промежуточную точку. Когда ясно, о какой из двух дуг идёт речь, используется обозначение без промежуточной точки. Обозначаются дуги так: u ALB, и AMB, и AB (рис. 3).

Дуга называется полуокружностью, если отрезок, соединяющий её кон­цы, является диаметром окружности. На рисунке 2 дуга ANB - полуокружность.

Для изображения окружности на чертеже пользуются циркулем. Чтобы провести окружность на местности, можно воспользоваться веревкой.

Часть плоскости, ограниченная окружностью, называется кругом (рис. 4).

Рис. 4

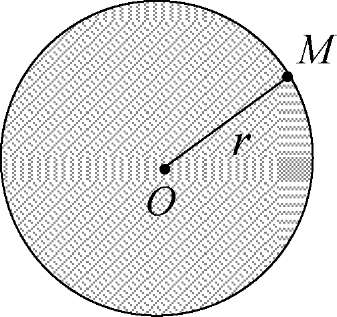
Возможны три случая взаимного расположения прямой и окружности в зависимости от соотношения между d — расстоянием от центра окружности до прямой и r — радиусом окружности, прямая и окружность имеют одну или две общие точки и не имеют ни одной общей точки.

1. случай: d < r (рис. 5). Если расстояние от центра окружности до прямой меньше радиуса окружности, то прямая и окружность имеют две общие точки (пересекаются в двух точках).

В этом случае прямая называется секущей по отношению к окружности. Секущая - это прямая, имеющая с окружность две общие точки, или секущая - это прямая, пересекающая окружность в двух точках.

2. случай: d = r (рис. 6). Если расстояние от центра окружности до прямой равно радиусу окружности, то прямая и окружность имеют только одну в одной точке общую точку (касаются).

В этом случае прямая называется касательной к окружности. Прямая, имеющая с окружностью только одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окруж­ности.

3. случай: d > r (рис. 7). Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общих точек

(не пересекаются).

d > r

Рис. 5

d < r

р - секущая

d = r

р - касательная А - точка касания Рис. 6

Рис. 7

Билет № 5

1. Теорема о сумме внутренних углов треугольника.

2. Касательная к окружности. Определение, свойства.

Вопрос № 1

Теорема о сумме внутренних углов треугольника. Следствия

Теорема. Сумма внутренних B a

A C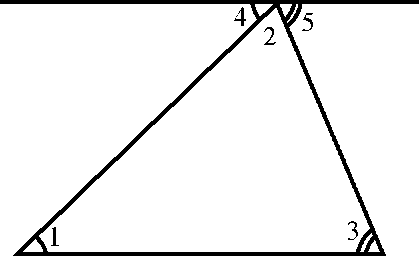

углов треугольника равна 180^о.

Дано: D АВС.

Доказать: ZА + ZВ + ZС = 180^о.

Доказательство

Через вершину В D АВС проведём прямую а || АС.

Z 1 = Z 4 как они являются накрест лежащими углами, образованными при пересечении параллельных прямых а и АС секущей АВ.

Z 3 = Z 5, так как они являются накрест лежащими углами, образован­ными при пересечении параллельных прямых а и АС секущей ВС.

^ 4 + Z 2 + Z 5 = 180^о, так как они образуют развёрнутый угол с верши­ной в точке В.

Учитывая, что ^ 4 = Z1, а ^ 5 = Z 3, получаем что ^ 1 + Z 2 + Z 3 = 180^о или ^А + ^ В + Z С = 180^о.

Итак, сумма внутренних углов треугольника равна 180^о.

Ч.т.д.

Следствия

1. В любом треугольнике либо все углы острые, либо два угла острые, а третий угол тупой, либо два угла острые, а третий угол прямой.

2. Если два угла одного треугольника соответственно равны двум углам друго­го треугольника, то и третьи углы треугольников равны.

3. Сумма острых углов прямоугольного треугольника равна 90^о.

4. В равнобедренном прямоугольном треугольнике каждый острый угол равен 45^о.

5. В равностороннем треугольнике каждый угол равен 60^о.

6. Внешний угол треугольника равен сумме двух внутренних углов, не смеж­ных с ним (теорема о внешнем угле треугольника).

Вопрос № 2

Касательная к окружности. Определение, свойства

Прямая, имеющая с окружностью только одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности. На рисунке 1 прямая р - касательная к окружности с центром О, А - точка касания.

Теорема о свойстве касательной к окружности

Теорема. Касательная к окружности перпендикулярна к радиусу, прове­дённому в точку касания.

Рис. 1

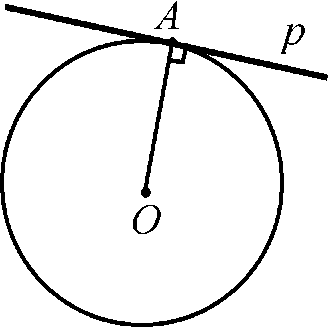
Дано: w (О;ОА)

р - касательная к окружности, А - точка касания.

Доказать: p X ОА.

Доказательство (методом от противного)

Предположим, что p X ОА (рис. 1).

В этом случае радиус ОА является наклонной к прямой р. Так как перпен­дикуляр, проведённый из точки О к прямой р, меньше наклонной ОА, то рас­стояние от центра О окружности до прямой р меньше радиуса. Следовательно, прямая р и окружность имеют две общие точки, т.е. р - секущая. Но это проти­воречит условию теоремы, что р - касательная к окружности.

Так как получили противоречие, то предположение, что p X ОА было не­верным, значит, p X ОА.

Итак, касательная к окружности перпендикулярна к радиусу, проведён­ному в точку касания.

Ч.т.д.

Верна и теорема, обратная теореме о свойстве касательной — признак касательной.

Теорема. Если прямая проходит через конец радиуса, лежащий на окружности, и пер­пендикулярна к этому радиусу, то она является касательной.

Дано: w (О;ОА), р, Ае р, p X ОА (рис. 1).

Доказать: р - касательная к w (О;ОА).

Доказательство

По условию р X ОА, ОА - радиус окружности, поэтому расстояние от центра окруж­ности до прямой р равно радиусу ОА. Следовательно, прямая и окружность имеют только одну общую точку. А это означает, что данная прямая р является касательной к окружности.

Итак, если прямая проходит через конец радиуса, лежащий на окружности, и пер­пендикулярна к этому радиусу, то она является касательной.

Ч.т.д.

На рисунке 2 проведены две касательные к окружности с центром О, про­ходящие через точку А и касающиеся окружности в точках В и С, при этом от­резки АВ и АС называются отрезками касательных, проведенных из точки А. Они обладают свойством, сформулированным в следующей теореме.

Теорема об отрезках касательных к окружности, проведенных из одной точки Теорема. Отрезки касательных к окружности, проведённые из одной точ­ки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности. Рис. 2

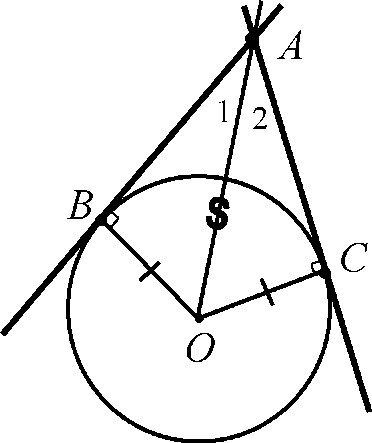
Дано: w (О;г), Ag w (О;г),

AB, AC - касательные к окружности, В и С - точки касания.

Доказать: АВ = ВС, Z1 =Z 2.

Доказательство

Так как касательная к окружности перпендикулярна к радиусу, проведён­ному в точку касания, то ^ АВО =Z АСО = 90°, а D АВО и D АСО - прямо­угольные (рис. 2).

Рассмотрим D АВО и D АСО. АО - общая сторона, ОВ = ОС как радиусы одной окружности. Следовательно, D АВО = D АСО по признаку равенства прямоугольных треугольников (по гипотенузе и катету).

В равных треугольниках соответствующие элементы равны, поэтому АВ = ВС и ^ 1 =Z 2.

Итак, отрезки касательных к окружности, проведённые из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.

Ч.т.д.

Билет № 6

1. Теорема о сумме углов выпуклого «-угольника.

2. Формула длины окружности. Запись, вывод.

Вопрос № 1

Многоугольник. Теоремы о сумме углов выпуклого n-угольника

Многоугольником называется фигура, составленная из отрезков так, что смежные отрезки не лежат на одной прямой, а несмежные отрезки не имеют общих точек.

Многоугольник называется выпуклым, если он лежит по одну сторону от каждой прямой, проходящей через две его соседние вершины.

Внутренним углом выпуклого многоугольника при данной вершине на­зывается угол, образованный его сторонами, сходящимися в этой вершине.

Внешним углом выпуклого многоугольника при данной вершине называ­ется угол, смежный с внутренним при этой вершине.

Сумма внутренних углов выпуклого n -угольника

Теорема. Сумма внутренних углов выпуклого многоугольника равна (п - 2) -180°, где п - число сторон многоугольника.

Дано: выпуклый «-угольник. Доказать: S_n = (n - 2) -180^о.

Доказательство

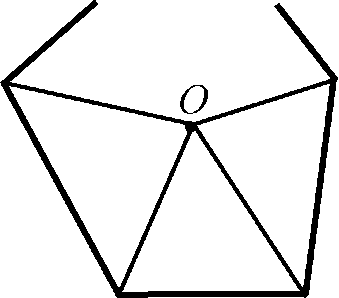
Внутри n-угольника возьмём произвольную точку О и соединим её со всеми вершинами. Многоугольник разобьётся на n треугольников с общей вер­шиной О.

Сумма углов каждого треугольника равна 180^о, следовательно, сумма углов всех треугольников равна 180^о«. В эту сумму, кроме суммы всех внутренних углов многоугольника, входит сумма углов треугольников при вершине О, рав­ная 360^о.

Таким образом, сумма всех внутренних углов многоугольника равна 180^о« - 360^о = (n - 2) -180^о.

Итак, S_n = (n - 2) -180^о.

Ч.т.д.

Сумма внешних углов выпуклого n -угольника

Теорема. Сумма внешних углов выпуклого многоугольника, взятых по одному при каждой вершине, не зависит от n и равна 360^о, где п - число сторон n-угольника.

Доказательство

Так как внешний угол многоугольника является смежным соответствую­щему внутреннему углу, а сумма смежных углов равна 180^о, то сумма внешних углов многоугольника равна:

180^о n - (n - 2) -180° = 180^о n - 180^о n + 360^о = 360^о.

С—' С .. J

^Y Y

внешние внутренние

и внутренние

Итак, сумма внешних углов выпуклого многоугольника, взятых по од­ному при каждой вершине, не зависит от n и равна 360^о, где п - число сторон n- угольника.

Ч.т.д.