Свойства функции распределения
1. 0 ≤ F(x) ≤ 1.
2.
Достигаются ли эти крайние значения? В
пределе – всегда (функция распределения
определена на всей числовой оси):
F(
) = 0,
F(
) = 1.
3. F – монотонно неубывающая функция (может только возрастать и не может убывать). Это легко доказать по определению.
4.
Полезность
введенного определения функции
распределения обусловлена следующим
очень важным свойством, позволяющим
через нее вычислять вероятность попадания
случайной величины Х
на заданный интервал
: Р(Х
) = F(β)
– F(α).
(Аналог
формулы Ньютона–Лейбница в интегральном
исчислении.)
Вопросы для самопроверки
Чем случайная величина отличается от случайного события?
Чем отличается дискретная случайная величина от непрерывной?
Дать определение закона (ряда) распределения дискретной случайной величины.
Какая случайная величина называется биномиально распределенной?
Дать определение математического ожидания случайной величины и объяснить его теоретико-вероятностный смысл.
Указать свойства математического ожидания.
Дать определение дисперсии случайной величины и объяснить теоретико-вероятностный смысл этого понятия.
Сформулировать свойства дисперсии.
Что называется функцией распределения случайной величины?
Сформулировать свойства функции распределения.
1.5. Непрерывные случайные величины
Непрерывной случайной величиной называется случайная величина, значения которой покрывают сплошным образом целый интервал на числовой оси, и функция распределения которой является кусочно-дифференцируемой функцией. Например, температура, замеренная в какой-либо точке пространства. Ее значения изменяются непрерывным образом. Другой пример – вес случайно взятого человека.
Плотность вероятности непрерывной случайной величины
Непрерывные
случайные величины исчерпывающим
образом описываются производной от
функции распределения, называемой
функцией плотности вероятности:
р(х) = 
F(x).
В свою очередь, зная р(х), можно найти F(x) через интеграл:
F(x) = 
.
Cвойства функции плотности вероятности
1. р(х) ≥ 0, как производная от монотонно возрастающей функции.
2. Площадь под графиком плотности вероятности равна единице:
.
3.
Функция плотности вероятности позволяет
находить вероятность попадания случайной
величины на заданный интервал (см.
свойство 4 функции распределения): Р(Х
)
=
= 
.
Осуществляя предельные переходы в определениях важнейших числовых характеристик случайных величин, получим формулы для вычисления математического ожидания непрерывной случайной величины:
и дисперсии непрерывной случайной величины:
.
Нормальное распределение
Нормальной
случайной величиной
Х = N(a,
)
называется непрерывная случайная
величина, имеющая плотность вероятности
следующего вида:
р(х) = 
).
Параметры a и носят простой смысл – это математическое ожидание и среднеквадратичное отклонение: а = М(N(а, )), 2 = D(N(а, )). График плотности вероятности нормальной случайной величины носит название кривой Гаусса, имеющей вертикальную ось симметрии, проходящую через точку а:
P(x)
x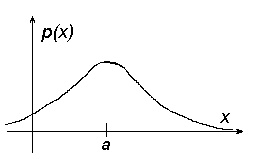
Для
случайной величины N(0,
1), являющейся важнейшей и всесторонне
изученной, практически применяемой
случайной величиной, составлены подробные
таблицы вероятностей, с которыми она
попадает в те или иные интервалы значений.
Так, Р({0
< N(0,
1) < х}) = Ф(х),
где Ф(х) = 
–
интегральная функция Лапласа.
Таблицы значений этой функции имеются
в каждом учебнике по теории вероятностей
и математической статистике. В свою
очередь
Р({
< N(a,
)
<
}) = Р(N(a,
)
) =
= Ф(( –а)/ ) – Ф(( –а)/ ).
Многие исследуемые на практике случайные величины очень хорошо моделируются с помощью нормальных случайных величин. Это, например, таблицы значений проб прочности бетона в теории железобетонных конструкций, ошибки результатов измерений теодолитом в геодезии, разброс скоростей и энергий молекул в газе (при изучении курса физики – кривая Гаусса), рост или вес случайно взятого человека. Другим примером служит какой-либо экономический показатель, величина которого описывается взаимодействием большого числа независимых друг от друга причин и факторов.