Воронка наибольшей вместимости
ЗАДАЧА
Из жестяного круга нужно изготовить коническую часть воронки. Для этого в круге вырезают сектор и остальную часть круга свертывают конусом (рис.31). Сколько градусов должно быть в дуге вырезаемого сектора, чтобы конус получился наибольшей вместимости?
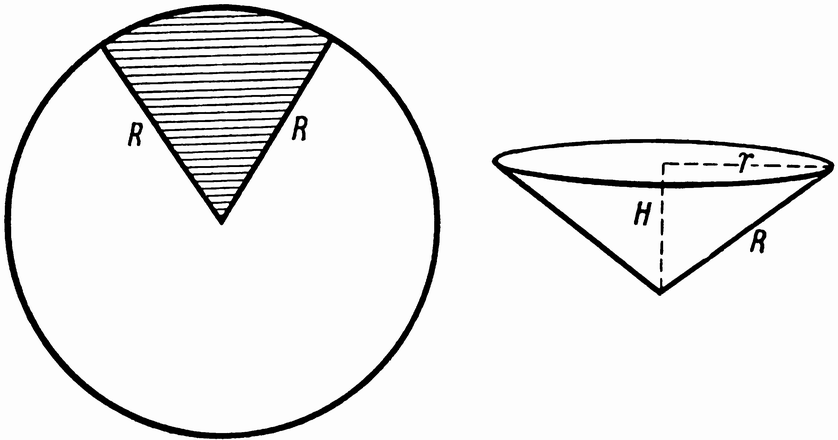
Рис. 31.
РЕШЕНИЕ
Длину дуги той части круга, которая свертывается в конус, обозначим через х (в линейных мерах). Следовательно, образующей конуса будет радиус R жестяного круга, а окружность основания будет равна x. Радиус r основания конуса определяем из равенства
2
r = x,
откуда
.
Высота конуса (по теореме Пифагора)
(рис. 31). Объем этого конуса имеет значение
.
Это выражение достигает наибольшей величины одновременно с выражением
.
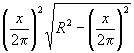и его квадратом
.
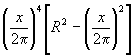Так как
есть величина постоянная, то (на основании доказанного в разделе "Когда произведение наибольшее?") последнее произведение имеет максимум при том значении х, когда
,
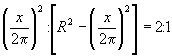откуда
,
и
.
В градусах дуга x 295° и, значит, дуга вырезаемого сектора должна содержать 65°.
<Paaaa
Самое яркое освещение
ЗАДАЧА
На какой высоте над столом должно находиться пламя свечи, чтобы всего ярче освещать лежащую на столе монету?
Рис. 32.
РЕШЕНИЕ
Может показаться, что для достижения наилучшего освещения надо поместить пламя возможно ниже. Это неверно: при низком положении пламени лучи падают очень отлого. Поднять свечу так, чтобы лучи падали круто, – значит удалить источник света. Наиболее выгодна в смысле освещения, очевидно, некоторая средняя высота пламени над столом. Обозначим ее через х (рис. 32). Расстояние ВС монеты В от основания С перпендикуляра, проходящего через пламя А, обозначим через а. Если яркость пламени i, то освещенность монеты согласно законам оптики выразится так:
,
где – угол падения пучка лучей АВ. Так как
,
то освещенность равна
.
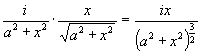Это выражение достигает максимума при том же значении х, что и его квадрат, т. е.
.
Множитель i2 как величину постоянную опускаем, а остальную часть исследуемого выражения преобразуем так:
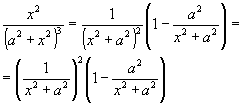
Преобразованное выражение достигает максимума одновременно с выражением
,
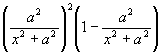так как введенный постоянный множитель а4 не влияет на то значение х, при котором произведение достигает максимума. Замечая, что сумма первых степеней этих множителей
есть величина постоянная, заключаем, что рассматриваемое произведение становится наибольшим, когда
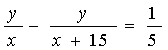
(см. "Когда произведение наибольшее?").
Имеем уравнение
.
Решив это уравнение, находим:
.
Монета освещается всего ярче, когда источник света находится на высоте 0,71 расстояния от проекции источника до монеты. Знание этого соотношения помогает при устройстве наилучшего освещения рабочего места.
<Paaaa
Глава восьмая. ПРОГРЕССИИ
<Paaaa
Древнейшая прогрессия
ЗАДАЧА
Древнейшая задача на прогрессии – не вопрос о вознаграждении изобретателя шахмат, насчитывающий за собой двухтысячелетнюю давность, а гораздо более старая задача о делении хлеба, которая записана в знаменитом египетском папирусе Ринда. Папирус этот, разысканный Риндом в конце прошлого столетия, составлен около 2000 лет до нашей эры и является списком с другого, еще более древнего математического сочинения, относящегося, быть может, к третьему тысячелетию до нашей эры. В числе арифметических, алгебраических и геометрических задач этого документа имеется такая (приводим ее в вольной передаче):
Сто мер хлеба разделить между пятью людьми так, чтобы второй получил на столько же больше первого, на сколько третий получил больше второго, четвертый больше третьего и пятый больше четвертого. Кроме того, двое первых должны получить в 7 раз меньше трех остальных. Сколько нужно дать каждому?
РЕШЕНИЕ
Очевидно, количества хлеба, полученные участниками раздела, составляют возрастающую арифметическую прогрессию. Пусть первый ее член х, разность у. Тогда
доля |
первого . . . . . . |
x |
" |
второго . . . . . . |
x + y |
" |
третьего . . . . . |
x + 2y |
" |
четвертого . . . . |
x + 3y |
" |
пятого . . . . . . |
x + 4y |
На основании условий задачи составляем следующие два уравнения:
После упрощений первое уравнение получает вид
х + 2у = 20,
а второе
11х = 2у.
Решив эту систему, получаем:
Значит, хлеб должен быть разделен на следующие части
<Paaaa