"Трудная задача"

Картина Богданова-Бельского "Трудная задача" известна многим, но мало кто из видевших эту картину

вникал в содержание той "трудной задачи", которая на ней изображена. Состоит она в том, чтобы устным счетом быстро найти результат вычисления:

.

Задача в самом деле нелегкая. С нею, однако, хорошо справлялись ученики того учителя, который с сохранением портретного сходства изображен на картине, именно С. А. Рачинского, профессора естественных наук, покинувшего университетскую кафедру, чтобы сделаться рядовым учителем сельской школы. Талантливый педагог культивировал в своей школе устный счет, основанный на виртуозном использовании свойств чисел. Числа 10, 11, 12, 13 и 14 обладают любопытной особенностью: .

Так как 100 + 121 + 144 = 365, то легко рассчитать в уме, что воспроизведенное на картине выражение равно 2.

Рис. 18.

Алгебра дает нам средство поставить вопрос об этой интересной особенности ряда чисел более широко: единственный ли это ряд из пяти последовательных чисел, сумма квадратов первых трех из которых равна сумме квадратов двух последних?

РЕШЕНИЕ

Обозначив первое из искомых чисел через х, имеем уравнение

x² + (х + 1)² + (x + 2)² = (х + 3)² + (x + 4)².

Удобнее, однако, обозначить через x не первое, а второе из искомых чисел. Тогда уравнение будет иметь более простой вид

(х – 1)² + x² + (x + 1)² = (х + 2)² + (x + 3)².

Раскрыв скобки и сделав упрощения, получаем:

x² – 10x – 11 = 0.

откуда

.

Существуют, следовательно, два ряда чисел, обладающих требуемым свойством: ряд Рачинского

10, 11, 12, 13, 14

и ряд

–2, –1, 0, 1, 2.

В самом деле,

(–2)² + (–1)² + 0² = 1² + 2².

<Paaaa

Какие числа?

ЗАДАЧА

Найти три последовательных числа, отличающихся тем свойством, что квадрат среднего на 1 больше произведения двух остальных.

РЕШЕНИЕ

Если первое из искомых чисел х, то уравнение имеет вид

(х + 1)² = х (х + 2) + 1.

Раскрыв скобки, получаем равенство

x² + 2x + 1 = x² + 2x + 1,

из которого нельзя определить величину х. Это показывает, что составленное нами равенство есть тождество; оно справедливо при любом значении входящей в него буквы, а не при некоторых лишь, как в случае уравнения. Значит, всякие три последовательных числа обладают требуемым свойством. В самом деле, возьмем наугад числа

17, 18, 19.

Мы убеждаемся, что

18² – 17 · 19 = 324 – 323 = 1.

Необходимость такого соотношения выступает нагляднее, если обозначить через х второе число. Тогда получим равенство

x² – 1 = (x + 1) (x – 1),

т. е. очевидное тождество.

<Paaaa

Глава седьмая. НАИБОЛЬШИЕ И НАИМЕНЬШИЕ ЗНАЧЕНИЯ

Помещаемые в этой главе задачи принадлежат к весьма интересному роду задач на разыскание наибольшего или наименьшего значения некоторой величины. Они могут быть решены различными приемами, один из которых мы сейчас покажем.

Русский математик П. Л. Чебышев в своей работе "Черчение географических карт" писал, что особенную важность имеют те методы науки, которые позволяют решать задачу, общую для всей практической деятельности человека: как располагать средствами своими для достижения по возможности большей выгоды.

<Paaaa

Два поезда

ЗАДАЧА

Два железнодорожных пути скрещиваются под прямым углом. К месту скрещения одновременно мчатся по этим путям два поезда: один со станции, находящейся в 40 км от скрещения, другой со станции в 50 км от того же места скрещения. Первый делает в минуту 800 м, второй – 600 м.

Через сколько минут, считая с момента отправления, паровозы были в наименьшем взаимном расстоянии? И как велико это расстояние?

РЕШЕНИЕ

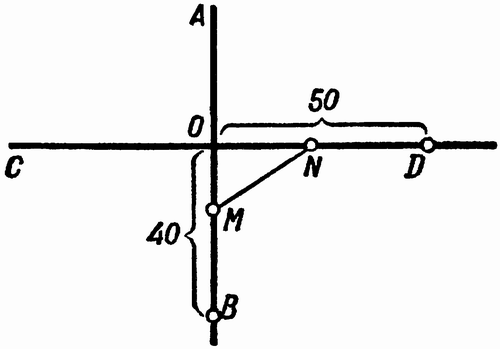
Начертим схему движения поездов нашей задачи. Пусть прямые АВ и CD – скрещивающиеся пути (рис. 19). Станция В расположена в 40 км от точки скрещения О, станция D – в 50 км от нее. Предположим, что спустя х минут паровозы будут в кратчайшем взаимном расстоянии друг от друга MN = m. Поезд, вышедший из В, успел к этому моменту пройти путь BM = 0,8x, так как за минуту он проходит 800 м = 0,8 км. Следовательно, ОМ = 40 – 0,8х. Точно так же найдем, что ON = 50 – 0,6x. По теореме Пифагора

MN = т = .

Рис. 19.

Рис. 20.

Возвысив в квадрат обе части уравнения

т =

и сделав упрощения, получаем:

х² – 124x + 4100 – т² = 0.

Решив это уравнение относительно х, имеем:

.

Так как х – число протекших минут – не может быть мнимым, то т² – 256 должно быть величиной положительной, или в крайнем случае равняться нулю. Последнее соответствует наименьшему возможному значению т, и тогда

т² = 256, т. е. т = 16.

Очевидно, что т меньше 16 быть не может, иначе х становится мнимым. А если т² – 256 = 0, то x = 62.

Итак, паровозы окажутся всего ближе друг к другу через 62 мин., и взаимное их удаление тогда будет 16 км.

Определим, как они в этот момент расположены. Вычислим длину ОМ; она равна

40 – 62 · 0,8 =  –9,6.

Знак минус означает, что паровоз пройдет за скрещение на 9,6 км. Расстояние же ON равно

50 – 62 · 0,6 = 12,8,

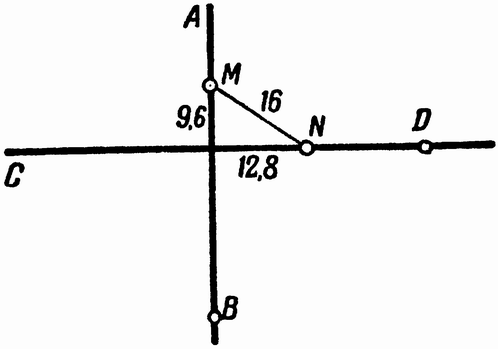
т. е. второй паровоз не дойдет до скрещения на 12,8 км. Расположение паровозов показано на рис. 20. Как видим, оно вовсе не то, какое мы представляли себе до решения задачи. Уравнение оказалось достаточно терпимым и, несмотря на неправильную схему, дало правильное решение. Нетрудно понять, откуда эта терпимость: она обусловлена алгебраическими правилами знаков.

<Paaaa