Номер автомашины

ЗАДАЧА

Прогуливаясь по городу, трое студентов-математиков заметили, что водитель автомашины грубо нарушил правила уличного движения. Номер машины (четырехзначный) ни один из студентов не запомнил, но, так как они были математиками, каждый из них приметил некоторую особенность этого четырехзначного числа. Один из студентов вспомнил, что две первые цифры числа были одинаковы. Второй вспомнил, что две последние цифры также совпадали между собой. Наконец, третий утверждал, что все это четырехзначное число является точным квадратом. Можно ли по этим данным узнать номер машины?

РЕШЕНИЕ

Обозначим первую (и вторую) цифру искомого числа через а, а третью (и четвертую) – через b. Тогда все число будет равно:

1000а + 100а + 10b + b = 1100а + 11b = 11(100а + b).

Число это делится на 11, а потому (будучи точным квадратом) оно делится и на 11². Иначе говоря, число 100а + b делится на 11. Применяя любой из двух вышеприведенных признаков делимости на 11, найдем, что на 11 делится число а + b. Но это значит, что

а + b = 11,

так как каждая из цифр а, b меньше десяти.

Последняя цифра b числа, являющегося точным квадратом, может принимать только следующие значения:

0, 1, 4, 5, 6, 9.

Поэтому для цифры а, которая равна 11 – b, находим такие возможные значения:

11, 10, 7, 6, 5, 2.

Первые два значения непригодны, и остаются следующие возможности:

b = 4,   a = 7; b = 5,   a = 6; b = 6,   a = 5; b = 9,   a = 2;

Мы видим, что номер автомашины нужно искать среди следующих четырех чисел:

7744, 6655, 5566, 2299.

Но последние три из этих чисел не являются точными квадратами: число 6655 делится на 5, но не делится на 25; число 5566 делится на 2, но не делится на 4; число 2299 = 121 · 19 также не является квадратом. Остается только одно число 7744 = 88²; оно и дает решение задачи.

<Paaaa

Делимость на 19

Обосновать следующий признак делимости на 19. Число делится без остатка на 19 тогда и только тогда, когда число его десятков, сложенное с удвоенным числом единиц, кратно 19.

РЕШЕНИЕ

Всякое число N можно представить в виде

N = 10x + y,

где х – число десятков (не цифра в разряде десятков, а общее число целых десятков во всем числе), у – цифра единиц. Нам нужно показать, что N кратно 19 тогда и только тогда, когда

N' = x + 2y

кратно 19. Для этого умножим N' на 10 и из этого произведения вычтем N; получим:

10N' – N = 10(x + 2y) – (10x + y) = 19y.

Отсюда видно, что если N' кратно 19, то и

N = 10N' – 19y

делится без остатка на 19; и обратно, если N делится без остатка на 19, то

10N' = N + 19y

кратно 19, а тогда, очевидно, и N' делится без остатка на 19.

Пусть, например, требуется определить, делится ли на 19 число 47 045 881.

Применяем последовательно наш признак делимости:

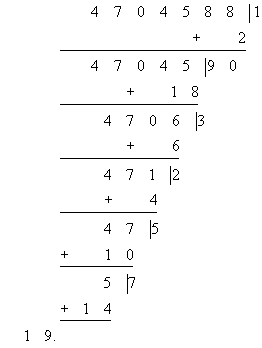
Так как 19 делится на 19 без остатка, то кратны 19 и числа 57, 475, 4712, 47063, 470 459, 4 704 590, 47 045 881.

Итак, наше число делится на 19.

<Paaaa

Теорема Софии Жермен

Вот задача, предложенная известным французским математиком Софией Жермен:

Доказать, что каждое число вида a⁴ + 4 есть составное (если а не равно 1).

РЕШЕНИЕ

Доказательство вытекает из следующих преобразований:

a⁴ + 4 = a⁴ + 4a² + 4 – 4a² = (a² + 2)² – 4a² = = (а² + 2)² – (2а)² = (а² + 2 – 2a)(a² + 2 + 2a).

Число а⁴ + 4 может быть, как мы убеждаемся, представлено в виде произведения двух множителей, не равных ему самому и единице [Последнее – потому, что а² + 2 – 2a = (a² – 2а + 1) + 1 = (a – 1)² + 1   1, если а   1.], иными словами, оно – составное.

<Paaaa

Составные числа

Число так называемых простых чисел, т. е. целых чисел, бóльших единицы, не делящихся без остатка ни на какие другие целые числа, кроме единицы и самих себя, бесконечно велико.

Начинаясь числами 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, ..., ряд их простирается без конца. Вклиниваясь между числами составными, они разбивают натуральный ряд чисел на более или менее длинные участки составных чисел. Какой длины бывают эти участки? Следует ли где-нибудь подряд, например, тысяча составных чисел, не прерываясь ни одним простым числом?

Можно доказать, – хотя это и может показаться неправдоподобным, – что участки составных чисел между простыми бывают любой длины. Нет границы для длины таких участков: они могут состоять из тысячи, из миллиона, из триллиона и т. д. составных чисел.

Для удобства будем пользоваться условным символом п!, который обозначает произведение всех чисел от 1 до п включительно. Например 5! = 1 · 2 · 3 · 4 · 5. Мы сейчас докажем, что ряд

[(n+1)!+2], [(n+1)!+3], [(n+1)!+4], ... до [(n+1)!+n+1] включительно

состоит из п последовательных составных чисел.

Числа эти идут непосредственно друг за другом в натуральном ряду, так как каждое следующее на 1 больше предыдущего. Остается доказать, что все они – составные.

Первое число

(n + 1)! + 2 = 1 · 2 · 3 · 4 · 5 · 6 · 7 ·... · (n + 1) + 2

– четное, так как оба его слагаемых содержат множитель 2. А всякое четное число, большее 2, – составное.

Второе число

(n + 1)! + 3 = 1 · 2 · 3 · 4 · 5 · 6 · 7·...· (n + 1) + 3

состоит из двух слагаемых, каждое из которых кратно 3. Значит, и это число составное.

Третье число

(n + 1)! + 4 = 1 · 2 · 3 · 4 · 5 · 6 · 7·...·(n + 1) + 4

делится без остатка на 4, так как состоит из слагаемых, кратных 4.

Подобным же образом устанавливаем, что следующее число

(n + 1)! + 5

кратно 5 и т. д. Иначе говоря, каждое число нашего ряда содержит множитель, отличный от единицы и его самого; оно является, следовательно, составным.

Если вы желаете написать, например, пять последовательных составных чисел, вам достаточно в приведенный выше ряд подставить вместо п число 5. Вы получите ряд

722, 723, 724, 725, 726.

Но это – не единственный ряд из пяти последовательных составных чисел. Имеются и другие, например,

62, 63, 64, 65, 66.

Или еще меньшие числа:

24, 25, 26, 27, 28.

Попробуем теперь решить задачу:

Написать десять последовательных составных чисел.

РЕШЕНИЕ

На основании ранее сказанного устанавливаем, что в качестве первого из искомых десяти чисел можно взять

1 · 2 · 3 · 4 · ... · 10 · 11 + 2 = 39 816 802.

Искомой серией чисел, следовательно, может служить такая:

39 816 802, 39 816 803, 39 816 804 и т. д.

Однако существуют серии из десяти гораздо меньших последовательных составных чисел. Так, можно указать на серию даже не из десяти, а из тринадцати составных последовательных чисел уже во второй сотне:

114, 115, 116, 117 и т. д. до 126 включительно.

<Paaaa