2.3. Другие виды аннуитетов Основные формулы и примеры

1). Аннуитет с выплатами в начале периода (рента пренумерандо) – платежи, одинаковой величины (СF), происходят через равные интервалы времени в начале периода (рис. 18). Первый платеж происходит сразу после заключения контракта (на начало первого периода, дату 0). Последний платеж – на начало последнего периода (дату (n–1)).

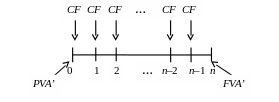
Рис. 18. Поток платежей для аннуитета с выплатами в начале периода

Текущую и будущую стоимости такого потока платежей можно найти по развернутым формулам, аналогичным (58), (59).

Текущая стоимость аннуитета с выплатами в начале периода. Каждый платеж умножаем на коэффициент дисконтирования и складываем (аналог формулы (58), первый платеж не дисконтируем, так как он относиться к дате 0, к которой приводим все платежи):

. (68)

Будущая стоимость аннуитета с выплатами в начале периода. Каждый платеж умножаем на коэффициент наращения и складываем (аналог формулы (59), на первый платеж проценты будут начисляться от момента 0 до момента n, т. е. всего n периодов; на второй платеж (n–1) периодов и т. д.):

, (69)

где CF – платеж в начале периода; r – доходность по альтернативному вложению за период; n – число периодов начисления (число платежей).

По сравнению с обыкновенным аннуитетом, в аннуитете с выплатами в начале периода проценты начисляются на один период больше, так как платежи вносятся раньше. Используем известные формулы обыкновенного аннуитета, начислив на них проценты путем умножения на коэффициент наращения за один период. Преобразованные формулы представлены в таблице 8.

Таблица 8

Аннуитет с выплатами в начале периода

Текущая стоимость	Будущая стоимость
Период платежей совпадает с периодом начисления процентов (p=k)
(70)	(71)
где PVA – рассчитано по формуле (61) или (58); FVA – рассчитано по формуле (62) или (59) для обыкновенного аннуитета; r – процентная ставка за период начисления.
Период платежей может не совпадать с периодом начисления процентов (pk)
(72)	(73)
где PVA – рассчитано по формуле (66); FVA – рассчитано по формуле (67) для обыкновенного аннуитета; r – годовая процентная ставка, начисляемая k раз в год; платежи происходят p раз в год.

2). Аннуитет с выплатами в середине периода – платежи, одинаковой величины (СF), происходят через равные интервалы времени в середине периода (рис. 19). Первый платеж происходит в середине первого периода (дата ). Последний платеж – в середине последнего периода (дата ( )).

По сравнению с обыкновенным аннуитетом, в аннуитете с выплатами в середине периода проценты начисляются на половину периода больше. Поэтому формулы обыкновенного аннуитета умножаем на коэффициент наращения за половину периода (таблица 9).

Таблица 9

Аннуитет с выплатами в середине периода

Текущая стоимость	Будущая стоимость
Период платежей совпадает с периодом начисления процентов (p=k)
(74)	(75)
где PVA – рассчитано по формуле (61) или (58); FVA – рассчитано по формуле (62) или (59) для обыкновенного аннуитета; r – процентная ставка за период начисления.
Период платежей может не совпадать с периодом начисления процентов (pk)
(76)	(77)
где PVA – рассчитано по формуле (66); FVA – рассчитано по формуле (67) для обыкновенного аннуитета; r – годовая процентная ставка, начисляемая k раз в год; платежи происходят p раз в год.

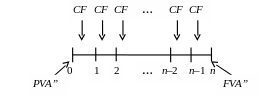
Рис. 19. Поток платежей для аннуитета с выплатами в середине периода

Пример 80. Найти текущую стоимость ежегодных платежей, если в течение 4 лет выплачивается по 45 000 руб. Рыночная ставка 10% годовых. Платежи происходят: а) в конце года; б) в середине года; в) в начале года.

Период платежей совпадает с периодом начисления процентов (p=k=1).

а) Для обыкновенного аннуитета используем формулу (61):

руб.

б) Для аннуитета с выплатами в середине периода используем формулу (74), значение PVA нашли в пункте (а):

руб.

в) Для аннуитета с выплатами в начале периода используем формулу (70), значение PVA нашли в пункте (а):

руб.

Пример 81. Найти накопленную через 4 года сумму, если в начале каждого полугодия на счет вкладывается по 25 000 руб. под 9% годовых, начисляемых ежемесячно.

Взносы раз в полгода (p=2), что за год составляет CF=25 0002=50 000 руб. Срок n=4 года. Проценты r=9%, начисляются k=12 раз в год. Период платежей не совпадает с периодом начисления процентов, поэтому в формулу (77) подставляем формулу (67).

Будущая стоимость аннуитета с выплатами в начале периода (pk):

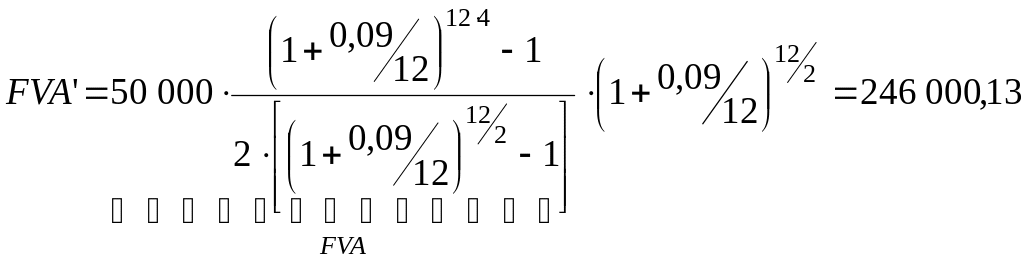руб.

3). Отложенный аннуитет (отсроченная рента) – платежи, одинаковой величины (СF), происходят через равные интервалы времени в конце периода. Первый платеж откладывается на t периодов. Последний платеж происходит на дату (t+n). Представляет собой обыкновенный аннуитет, сдвинутый на (t–1) периодов вперед. Поэтому на рисунке 20 покажем в сравнении отложенный аннуитет и обыкновенный аннуитет.

Сдвиг во времени влияет на значение текущей стоимости потока платежей. Найденная по формулам обыкновенного аннуитета текущая стоимость потока платежей попадает на период раньше, чем первый платеж (дата (t–1), которая соответствует дате 0 для обыкновенного аннуитета). Поэтому текущую стоимость необходимо дисконтировать на (t–1) периодов.

Текущая стоимость отложенного аннуитета, если период платежей совпадает с периодом начисления процентов (p=k):

, (78)

где PVA – рассчитано по формуле (61) или (58) для обыкновенного аннуитета; r – процентная ставка за период начисления; t – дата первого платежа (в периодах).

Текущая стоимость отложенного аннуитета, если период платежей может не совпадать с периодом начисления процентов (pk):

, (79)

где PVA – рассчитано по формуле (66) для обыкновенного аннуитета; r – годовая процентная ставка, начисляемая k раз в год; t – дата первого платежа (в годах).

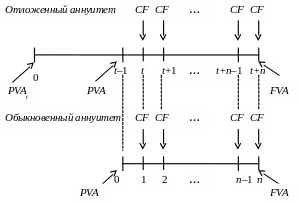
Рис. 20. Сравнение во времени отложенного и обыкновенного аннуитетов

Будущая стоимость отложенного аннуитета

, (80)

где FVA – будущая стоимость обыкновенного аннуитета, рассчитанная по формуле (59), (62) или (67), так как сдвиг во времени не отражается на величине будущей стоимости отложенного аннуитета.

Пример 82. Найти размер кредита, если для его погашения необходимо с 4 по 10 месяцы выплачивать по 8000 руб., ставка 20% годовых.

График платежей показан на рисунке 21.

Взносы по 8000 руб. вносятся ежемесячно (p=12 раза в год), следовательно, годовой платеж равен CF=800012=96 000 руб. платежи идут 7 месяцев, поэтому года. Проценты r=20%, начисляются k=1 раз в год.

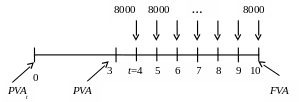
Рис. 21. Отложенный аннуитет

1. Текущую стоимость находим по формуле (66), так как (pk):

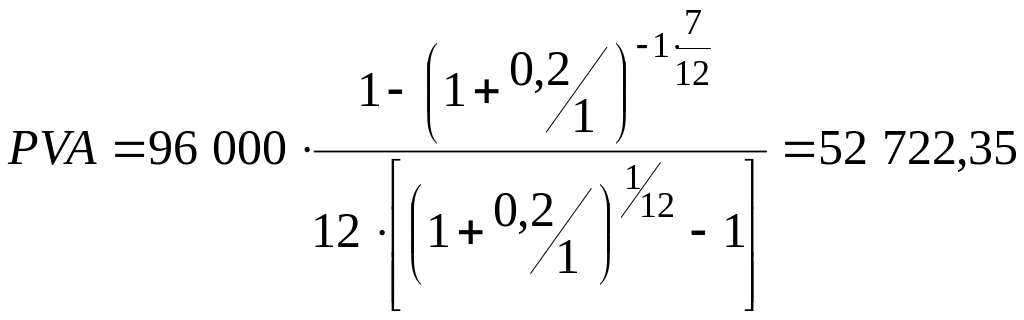руб.

Полученная текущая стоимость обыкновенного аннуитета относиться к дате 3 месяца или года (на период раньше, чем первый платеж).

2. Дисконтируем найденное PVA на 0 по формуле (79).

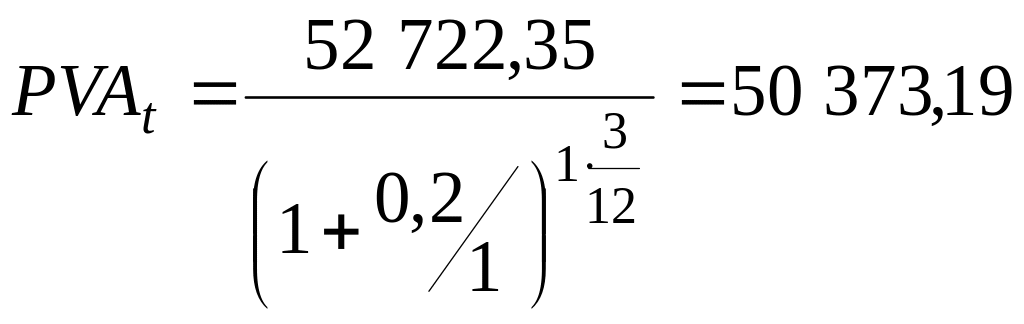руб.

3. За отсрочку платежа заплатили

руб.

4). Вечная рента – имеет неограниченное число платежей одинаковой величины (СF), происходящих через равные интервалы времени в конце периода. Примером может быть облигация без срока погашения, купонные платежи по которой представляют собой поток платежей.

Текущая стоимость вечной ренты (n):

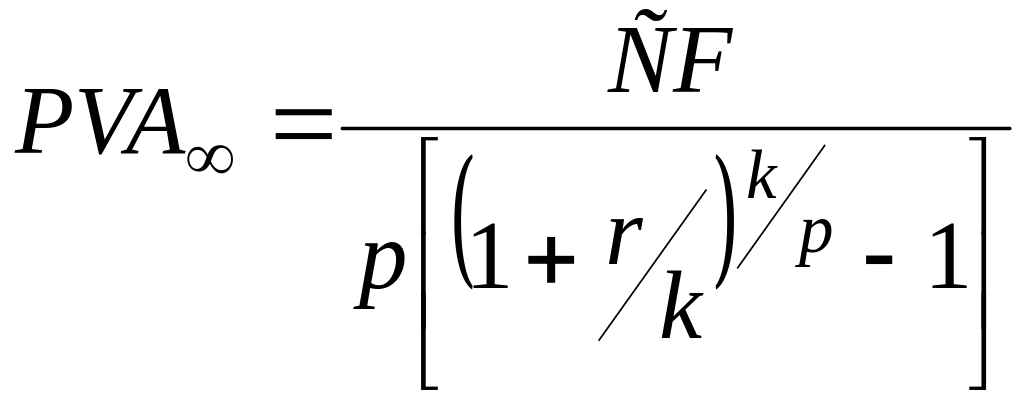, (81)

где CF – годовой платеж, может вноситься частями (p раз в течение года); r – годовая (номинальная) процентная ставка, начисляемая k раз в год; – ставка за период начисления

Будущая стоимость вечной ренты .

Пример 83. Определить, сколько надо инвестировать под 10% годовых с ежемесячным начислением, чтобы в конце каждого месяца получать по 20 000 руб. процентных платежей.

Годовой платеж равен CF=20 00012= 240 000 руб.; проценты r=10%, начисляются k=12 раз в год. Подставляем данные в формулу (81):

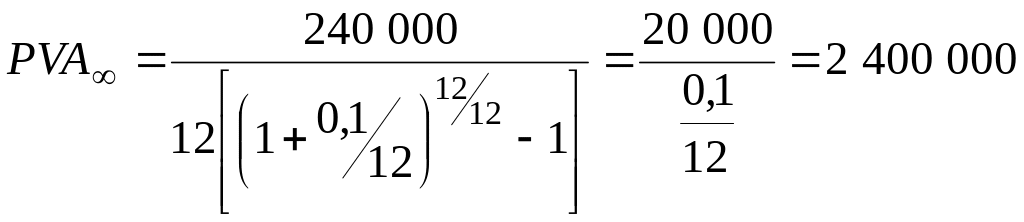руб.

5). Аннуитет с начислением простых процентов – платежи, одинаковой величины (CF), происходят через равные интервалы времени в конце периода (рис. 15). При расчете текущей и будущей стоимости используется простая процентная ставка.

Текущая стоимость аннуитета с начислением простых процентов (каждый платеж CF умножаем на коэффициент дисконтирования по простым процентам (формула (5)) и складываем):

, (82)

где r – доходность по альтернативному вложению за период.

Будущая стоимость аннуитета с начислением простых процентов (каждый платеж CF умножаем на коэффициент наращения по простым процентам (формула (4)) и складываем):

. (83)

Формулу (83) можно свернуть, как сумму арифметической прогрессии

. (84)

Пример 84. Найти текущую и будущую стоимость потока платежей, если в конце каждого года в течение 3 лет на депозит инвестируется по 100 000 руб. под простые проценты 10% годовых (рис. 10).

Текущая стоимость аннуитета с начислением простых процентов (82):

руб.

Будущая стоимость аннуитета с начислением простых процентов (84):

руб.

6). Смешанный аннуитет – платежи, одинаковой величины (CF), происходят р раз в год через равные интервалы времени в конце периода. Проценты начисляются следующим образом. В течение года на вносимые платежи начисляются простые проценты, а за годовые периоды начисляются сложные проценты.

Будущую стоимость смешанного аннуитета находим следующим образом.

1. Будущую стоимость за год рассчитываем, как будущую стоимость аннуитета с начислением простых процентов (FVA_пр). Формулу (84) перепишем в виде:

, (85)

где i – ставка простых процентов за период; p – число периодов в году; CF – платеж за период.

2. Накопленная за год стоимость (FVA_год) рассматривается как годовой платеж обыкновенного аннуитета. Будущая стоимость смешанного аннуитета рассчитывается по формуле (62), представленной в виде:

, (86)

где r – сложная процентная ставка за год; n – число лет.

Пример 85. Компания ежемесячно вносит в банк по 40 000 руб., на которые начисляются простые проценты по ставке 1% в месяц. За целые годовые периоды начисляются сложные проценты по ставке 6% годовых. Определить накопленную за 3 года сумму.

1. Будущая стоимость за год при начислении простых процентов (85), взносы по 40 000 руб. вносятся ежемесячно (p=12 раз в год), i=1% в месяц:

руб.

2. Будущая стоимость смешанного аннуитета (86), r=6% в год, n=3 года:

руб.

Через 3 года накопится 1 612 175,04 руб.