6. Электростатика диэлектриков.

6.1. Теорема единственности для решения граничных задач электростатики диэлектриков. Докажем единственность решения задачи о потенциале в среде, состоящей из некоторого числа диэлектриков без пространственной диперсии с постоянными диэлектрическими проницаемостями (Рис. 6.1). В каждой из областей потенциал удовлетворяет уравнению Пуассона

, (6.1)

где - плотность зарядов на границе - го диэлектрика с проводниками, - плотность сторонних зарядов в области . На границе раздела сред должны выполняться граничные условия

, (6.2)

где - плотность поверхностного заряда. Так как , то первое из условий (6.2) будет выполнено, если на границе раздела сред выполнено условие

. (6.3)

Второе условие в (6.2) перейдет в следующее

. (6.4)

Таким образом, задача электростатики диэлектриков сводится к решению уравнения (6.1) с известными функциями с учетом граничных условий (6.3), (6.4). Утверждается, что решение такой задачи единственно, потенциал находится с точностью до постоянного слагаемого. Последнее не влияет на электрическое поле, так как . Доказательство утверждения проводится способом от противного. Пусть и - два различных решения задачи, причем . Так как и удовлетворяют уравнению (6.1) с одними и теми же источниками, то . На границах потенциал будет удовлетворять условиям

, . (6.5)

Воспользуемся формулой Грина

.

где - замкнутая поверхность, охватывающая объем , занимаемый диэлектриком с проницаемостью , - внешняя по отношению к нормаль на поверхности . Функции заданы в объеме . Возьмем . Формула Грина с учетом однородного уравнения Пуассона для и суммирования по дает. (6.6)

При написании этого соотношения учтено, что интегрирование по поверхности возникает дважды: один раз, когда формула Грина пишется для объема с диэлектриком , а другой раз, для соседнего объема с диэлектриком . Нормали обладают свойством . С учетом этого свойства и второго граничного условия в (6.5) правая часть в (6.6) обращается в ноль. Имеем

.

Так как , то из равенства интеграла нулю следует, что

,

а это означает единственность решения рассматриваемой задачи.

6.2. Потенциал точечного заряда в присутствии диэлектрического полупространства. Смещение зарядов в молекулах однородного безграничного изотропного диэлектрика, помещенного в электростатическое поле, приводит к уменьшению результирующего поля в диэлектрике. Если диэлектрик ограничен, то изменение поля не сводится к масштабному уменьшению. Как правило, происходит существенное изменение пространственной структуры поля. При решении таких задач используется принцип единственности задач электростатики. Если с помощью суперпозиции электростатических полей удается удовлетворить граничным условиям на поверхности диэлектрика, то эта суперпозиция представляет собой истинное поле.

Определим потенциал, создаваемый точечным зарядом в присутствии диэлектрического полупространства с плоской границей (Рис. 6.2). Используем метод изображений. При этом идея использования фиктивных зарядов (изображений) несколько отличается от идеи изображений в задачах электростатики проводников (раздел 5.6). Считаем, что напряженность поля в вакууме будет такой же, как в отсутствии диэлектрика, но при наличии зеркального (фиктивного заряда) . Этот заряд помещается в точку в диэлектрике, точки и находятся на одинаковом расстоянии от границы раздела . Относительная диэлектрическая проницаемость этого диэлектрика . Реальный заряд находится в вакууме в точке .

Далее, предполагаем, что поле в диэлектрике будет таким же, как и поле дополнительного фиктивного заряда в неограниченном диэлектрике (без вакуумного полупространства) и расположенном в точке (это точка расположения реального заряда). На Рис. 6.2 и - это точки наблюдения соответственно в вакууме и в диэлектрике. Итак, предполагаем, что потенциалы и в вакууме и диэлектрике определяются формулами

,

В этих соотношениях имеются два неизвестных параметра и .Потенциалы и удовлетворяют уравнениям электростатики. Эти представления будут давать решение задачи, если выполняются граничные условия на поверхности диэлектрика. С этой целью подбираются величины пока еще произвольных двух констант и . Непрерывность тангенциальной составляющей электрического поля эквивалентна непрерывности потенциала. На границе раздела точки и совпадают и . Непрерывность потенциала обеспечивается выполнением условия

. (6.7)

Второе граничное условие это непрерывность нормальной составляющей вектора электрической индукции . Для вектора электрической индукции в двух полупространствах можно получить представления

, .

На границе диэлектрика и из условия получаем

. (6.8)

Из условий (6.7) и (6.8) находим искомые величины

, .

Теорема единственности обеспечивает истинность построенного решения.

6.3. Диэлектрический шар в однородном электрическом поле. Рассмотрим задачу о модификации однородного электростатического поля (Рис. 6.3) в которое помещается диэлектрический шар радиуса с диэлектрической проницаемостью . Проницаемость окружающей среды . При внесении диэлектрического объекта в однородное поле, поле внутри его, вообще говоря, становится неоднородным. В этом отношении данная задача является «экзотической» - будет показано, что поле внутри диэлектрического шара окажется однородным. Введем сферическую систему координат, полярная ось которой проходит через центр шара по направлению поля .Очевидно, что задача обладает осевой симметрией, ее решение не зависит от азимутального угла. Потенциал во внешней среде будем искать в виде суперпозиции

,

где - потенциал постоянного внешнего поля, - потенциал, создаваемый шаром. Потенциал внутри шара обозначим . Свободные заряды в диэлектриках отсутствуют, поэтому потенциалы и удовлетворяют однородному уравнению Пуассона. Общее решение этого уравнения можно представить в виде разложения по полиномам Лежандра (см. раздел 5.8 «Метод разделения переменных»)

, .

Потенциалы и должны удовлетворять условиям конечности их величин:

конечно при , конечно при . Это обеспечивается при . Получаем представления

,

.

На поверхности шара при эти потенциалы должны удовлетворять условиям

,

вытекающим из граничных условий для и . Приходим к уравнениям

. , ,

из которых в силу ортогональности полиномов Лежандра будем иметь систему двух уравнений для определения и

. (6.9)

Непосредственной проверкой можно убедиться, что эта система благодаря ортогональности полиномов Лежандра имеет ненулевое решение только при одном значении и (6.9) и принимает вид

, .

Решение этой системы дает

, .

В результате потенциал , описывающий возмущающее действие диэлектрического шара в области имеет вид потенциала диполя, помещенного в центр шара

, где

.

Для потенциала внутри шара имеем

и электрическое поле внутри шара представляется в виде

.

Таким образом, если в однородное поле вносится диэлектрический шар, то в нем создается однородное поле. Оно отличается от внешнего поля в раз. Возникает вопрос, при каких еще формах диэлектрика соблюдается свойство однородности? Оказывается, что это будет для диэлектрика в форме эллипсоида и бесконечного цилиндра, ось которого направлена вдоль внешнего поля. В отличие от , поле не зависит от размера диэлектрического шара. При имеем .

Так как это поле в диэлектрическом шаре, то полю можно придать смысл эффективного или действующего поля (поля, действующего на диэлектрический шар, моделирующий молекулу, подробнее об этом будет сказано в разделе 6.6)

. (6.10)

6.4. Потенциал распределенных зарядов. Уравнения электростатики для случая распределенной плотности сторонних зарядов , имеют вид

.

Потенциал удовлетворяет уравнению Пуассона

.

В случае точечного заряда и . Если - непрерывная функция координат, то заряд , сосредоточенный в бесконечно малом объеме можно считать точечным. Он создает потенциал

,

где - расстояние от элемента до точки наблюдения . Потенциал, создаваемый объемным распределением зарядов и поверхностным распределением зарядов , получается как суперпозиция соответствующих вкладов:

.

6.5. Полярные и неполярные молекулы в диэлектрике. Уменьшение поля в диэлектрике по сравнению с вакуумом (при тех же сторонних зарядах) связано со смещением зарядов в молекулах диэлектрика под действием электрического поля. Такое смещение зарядов приводит к возникновению у молекул направленного вдоль поля дипольного момента. При этом следует различать два принципиально различных типа молекул. Молекула одного типа (неполярные) сами по себе в отсутствии поля не обладают дипольным моментом, но дипольный момент у них возникает под действием поля. Поле как бы растягивает молекулу и раздвигает ее заряды. Положительные заряды смещаются по полю, а отрицательные против поля. При не очень сильных полях (в линейном приближении) дипольный момент неполярной молекулы оказывается пропорциональным напряженности электрического поля: , где - коэффициент поляризуемости молекулы.

Молекулы другого типа (полярные) обладают собственным (спонтанным) дипольным моментом при отсутствии внешнего поля. Хотя молекулы полярного диэлектрика и обладают спонтанным дипольным моментом, направления дипольных моментов отдельных молекул у полярных газов, жидкостей и ряда твердых диэлектриков распределены в отсутствие поля хаотически. Поэтому сумма дипольных моментов всех молекул в отсутствие поля равна нулю. Если полярную молекулу поместить в электрическое поле , то на нее будет действовать пара сил с моментом . Эта пара вращает диполь, стремясь расположить его вдоль поля. Таким образом, действие поля в случае полярного диэлектрика является прежде всего ориентирующим. Поле стремится ориентировать дипольные моменты отдельных молекул вдоль поля. Конечно, полярные молекулы, так же как и неполярные молекулы, могут деформироваться под действием внешнего поля. Однако, этот эффект является второстепенным по сравнению с ориентационным.

6.6. Поляризация плотных неполярных диэлектриков. Формулы Клаузиуса – Моссотти и Лоренца. В разделе 6.5 при обсуждении свойств неполярных диэлектриков подразумевалось, что в формуле для дипольного момента отдельной молекулы в случае слабых полей имеет место представление

,

поле имеет смысл среднего по пространству поля (это поле присутствует в уравнениях Максвелла), .

В случае полей малой амплитуды (линейное приближение), эту формулу можно представить в следующем альтернативном виде

,

где , - эффективное или действующее поле – поле действующее в той точке, где расположена молекула (при этом предполагается что сама молекула из этой точки удалена, поле присутствует в уравнении движения среды). Различие между и тем больше, чем больше плотность частиц в диэлектрике. Это следует из формулы (6.10).

Суммарный дипольный момент единицы объема это вектор поляризации

, (6.11)

где - концентрация неполярных молекул. В слабых полях (в линейном приближении) имеет место линейная связь между , и вектором поляризации . В общем случае такую связь можно представить в виде

, (6.12)

где . Второе равенство в(6,12) является следствием линейности теории, и оно дает связь между и

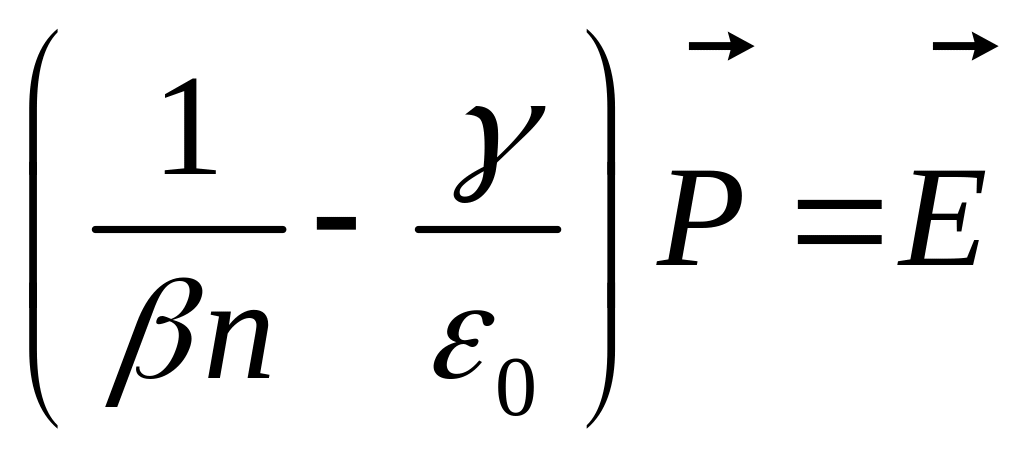, . (6.13)

Так как , то получаем представление для вектора электрической индукции

,где

.

Эту формулу можно преобразовать, представив в виде

.

Экспериментальные исследования показывают, что . Если взять , то получим известную формулу Клаузиуса – Моссотти

, (6.14)

дополнительно из (6.13) получается формула Лоренца

. (6.15)

Соотношение (6.13) принимает вид

.

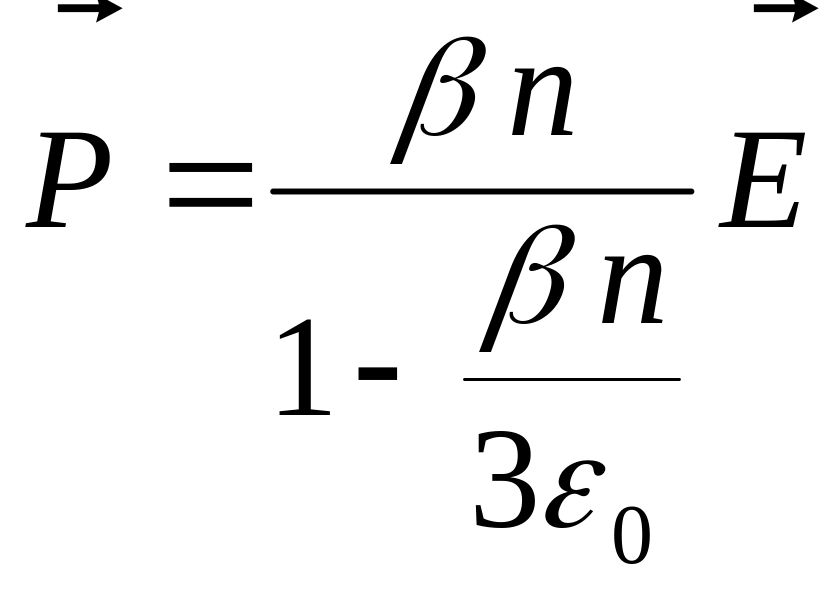С учетом (6.14) и (6.15) получаем выражение

,

Если молекулы в диэлектрике удалить и на их месте сделать сферические вакуумные полости произвольного размера, то представление для в таком приближении дается формулой (6.10), где под следует понимать среднее по пространству поле

.

Это подтверждает возможность моделирования неполярной молекулы сферической вакуумной полостью.

6.7. Поляризация полярных диэлектриков. Рассмотрим теперь газ, состоящий из одинаковых полярных молекул. Электрическое поле стремится ориентировать собственные дипольные моменты молекул по полю. Этой тенденции препятствует тепловое движение молекул. При отсутствии внешнего поля дипольные моменты ориентированы хаотически, все направления равновероятны, поэтому вектор поляризации в таком состоянии .

При внешне поле создает преимущественное направление для ориентации, при суммировании этих моментов необходимо учитывать вероятность распределения диполей по разным направлениям дипольных моментов . Перпендикулярные внешнему полю составляющие дипольных моментов молекул из-за их равновероятного распределения по углу не дают вклада в полный дипольный момент сферического объема.

Модуль полного дипольного момента единичного сферического объема в этом случае будет определяться по формуле

, , (6.16)

где - угол между векторами и . Угол является полярным углом в выбранной сферической системе координат, - элемент телесного угла, - азимутальный угол, - функция плотности вероятности распределения дипольных моментов по углам , - параллельная внешнему полю составляющая дипольного момента молекулы.

Если молекулы находятся в состоянии статистического равновесия, то функция плотности вероятности определяется формулой Больцмана

, (6.16а)

где - нормировочный множитель, - постоянная Больцмана, - температура, - потенциальная энергия полярной молекулы во внешнем поле, она минимальна при и она максимальна при . Нелинейная зависимость (6.16а) приводит к возникновению нелинейной связи . Это соответствует учету нелинейных эффектов в электростатике полярных диэлектриков. В результате имеем

.

Нормировочный множитель находится из условия

,

где -концентрация молекул. Получаем уравнение для определения

.

Для определения вектора поляризации в формуле (6.16) необходимо вычислить интеграл

Получается представление для абсолютной величины вектора поляризации

, (6.17)

где - функция Ланжевена,

.

Направление вектора поляризации совпадает с направлением поля . Получим представление для вектора поляризации и для диэлектрической проницаемости в предельном случае слабого поля и большой энергии теплового движения молекул:

, .

При этом имеем , .

Выражение для диэлектрической проницаемости получается из представления

, откуда следует

, .

Диэлектрическая проницаемость полярных диэлектриков в отличие от неполярных диэлектриков зависит от температуры. Поэтому если экспериментально установлена зависимость диэлектрической проницаемости от температуры в слабых полях, то это значит, что диэлектрик состоит из полярных молекул.

Другая предельная ситуация соответствует сильному полю, когда наступает эффект насыщения (все диполи ориентированы по полю):

, , , .

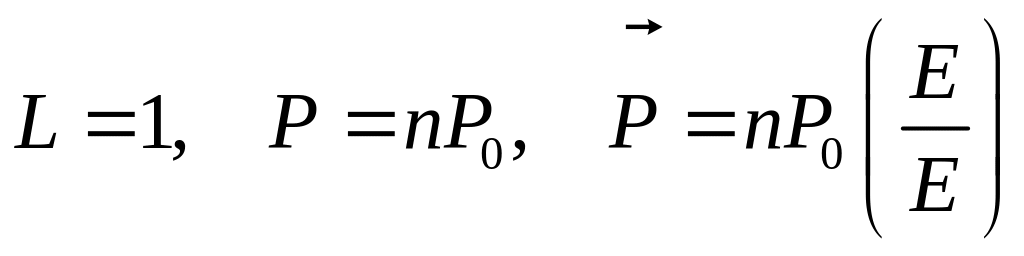Зависимость диэлектрической проницаемости полярного диэлектрика от поля отражает нелинейный характер поляризуемости таких сред.