10.15. Дисперсионное уравнение для волн в анизотропной среде. Свойства плоских волн в однородной анизотропной среде.

1. Прейдем к изучению волн малой амплитуды (линейное приближение) в анизотропных однородных средах. В таких средах векторы индукций и в общем случае не параллельны соответствующим полям и , диэлектрическая и магнитная проницаемости сред являются не скалярными, а тензорными величинами. Для Фурье – образов полей имеет место связь

.

Зависимость функций от является признаком наличия пространственной дисперсии, а зависимость от указывает на временную дисперсию. В этом разделе ограничимся рассмотрением веществ, анизотропных по отношению только электрическим свойствам и будем считать, что . Если тензор - симметричный т.е. , то всегда можно выбрать три взаимно перпендикулярных направления таким образом, что если направить вдоль них координатные оси , то тензор примет диагональную форму

,

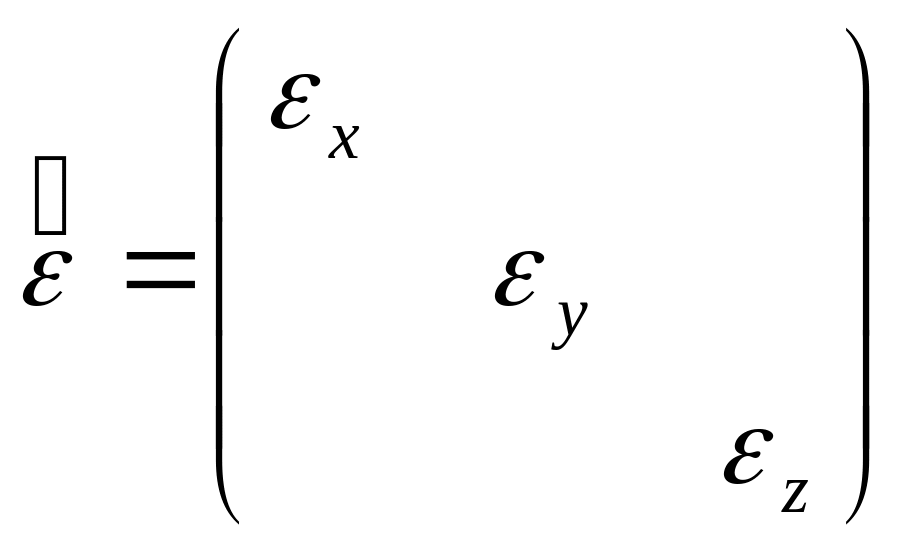где не выписанные элементы – нули. Такие направления называются главными диэлектрическими осями. Для кубических кристаллов все три главные диэлектрические проницаемости совпадают, выбор осей произволен, такой кристалл по электромагнитным свойствам не отличается от изотропной среды. Для одноосного кристалла совпадают две главные проницаемости (например )и выбор соответствующих двух осей ограничен лишь тем, чтобы они лежали в базисной плоскости (в данном примере это ). В двухосном кристалле все три главные проницаемости различны и отсутствует произвол в выборе главных осей. Главные оси, и только, они, обладают тем замечательным свойством, что если поле направлено вдоль одной из них, то индукция, как в изотропном случае, параллельна полю. При изменении частоты могут изменяться не только главные диэлектрические проницаемости, но и сами направления главных осей (в этом случае имеется дисперсия осей). Более сложный вид анизотропии существует в ситуации .

Анизотропия может иметь естественные и искусственные причины. При деформации изотропного тела в нем образуется выделенное направление, – возникают свойства одноосного кристалла (Зеебек 1813 г. Брюстер 1815 г.). Это явление используется при оптическом контроле напряжений в изделиях. Если имеется жидкая взвесь хаотически ориентированных анизотропных по форме частиц, то такая среда обладает изотропными свойствами. При создании потока возникает выделенное направление, степень упорядочения и анизотропия пропорциональны градиентам скорости (Максвелл 1873 г.). При помещении первоначально изотропных тел в однородное постоянное электрическое поле возникает анизотропия, пропорциональная квадрату (электрический эффект Керра 1875 г.). Аналогичный эффект возникает и в однородном постоянном магнитном поле (эффект Коттона - Мутона). Плазма, находящаяся во внешнем магнитном поле приобретает анизотропные свойства. При этом проявляется свойство магнитной активности: компоненты тензора комплексные функции даже при отсутствии диссипации. Характер анизотропии плазмы сильно зависит от частоты (обыкновенная и необыкновенная волны, или альфвеновская и магнитозвуковые волны,…)

2. Вопрос о возможных видах волн и об их свойствах можно решить на основе анализа дисперсионного уравнения для плоских волн (Фурье – образов полей). Из дисперсионного уравнения находится связь между волновым вектором и частотой. Это позволяет исследовать свойства фазовых и групповых скоростей в зависимости от параметров среды и направления распространения. После преобразования Фурье, однородные уравнения Максвелла можно привести к виду

(10.70)

где . Векторы и в плоской волне (Фурье - образы) ортогональны волновому вектору. Поле не обладает этим свойством в анизотропной среде, оно может иметь продольную (вдоль направления ) составляющую. Отметим, что в изотропной среде поле имеет продольную составляющую только при (это дисперсионное уравнение продольных волн). Это соотношение является прямым следствием уравнения при .

Система (10.70) с учетом формулы

приводится к однородному алгебраическому векторному уравнению для фурье – образа вектора электрического поля

`(10.70.А) или

, (10.71)

где , - символ Кронекера. Условие существования ненулевого решения возможно при условии равенства нулю определителя системы

.

Это уравнение и называется дисперсионным.

3. В частном случае изотропной среды представим вектор электрического поля в виде суммы двух слагаемых , где , . Дисперсионное уравнение разбивается на два. В уравнении (10.71.А) имеем значит дисперсионное уравнение для продольной волны имеет вид

.

Это соотношение можно получить непосредственно из уравнения , так как для продольной волны оно принимает вид . В продольной волне нет магнитного поля (имеет место уравнение ).

Для поперечной волны из (10.70.А) при следует

5. Рассмотрим одноосный кристалл.

.

Главную диэлектрическую ось (она совпадает с осью симметрии кристалла, и ее называют оптической осью кристалла) обозначим . Вращением системы координат добьемся того, что вектор «ляжет» в плоскость :

,

где - угол между осью и волновым вектором . Система алгебраических уравнений (10.71) для Фурье – образов поля имеет вид

Уравнение для «отщепляется» от остальной системы. Из него следует дисперсионное уравнение для поперечной электромагнитной волны (обыкновенной волны) и представление для волнового числа этой волны

.

В такой волне анизотропия не проявляется.

Во второй волне (необыкновенной) вектор имеет как продольную (вдоль оптической оси) так и поперечную компоненты. Эта волна является продольно – поперечной. Компоненты поля описываются системой уравнений

ненулевое решение системы возможно при условии равенства нулю ее определителя. Получаем представление для волнового числа необыкновенной волны

.

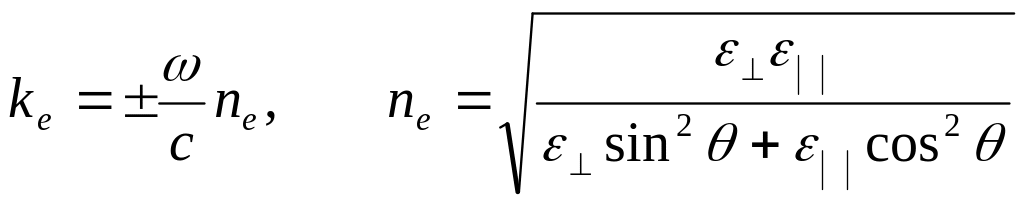Где - показатель преломления необыкновенной волны, он зависит от угла . Фазовая скорость так же зависит от угла . В предельном случае необыкновенная волна переходит в обыкновенную волну. Так как показатели преломления обыкновенной и необыкновенной волн различные, то при падении плоской волны из изотропной среды на границу с анизотропной средой, в последней волна «распадается» на обыкновенную и необыкновенную. Они распространяются под разными углами к границе раздела (эффект двойного лучепреломления).

10.16. Нелинейное дисперсионное уравнение. При описании нелинейных периодических волновых процессов вводится понятие нелинейное дисперсионное уравнение. Это обобщение соответствующего понятия линейной теории. При этом нелинейное дисперсионное уравнение получается, не опираясь на преобразование Фурье. Нелинейное дисперсионное уравнение получается как условие существования периодического решения. В случае непериодических решений, в линейной теории дисперсионное уравнение существует, а в нелинейной теории дисперсионного уравнения нет.

Рассмотрим конкретный пример. Получим условие существования периодического решения уравнения Кортевега-де Вриза (1895). Это простейшее уравнение, учитывающее влияние нелинейности и дисперсии. По существу будет анализироваться ситуация, когда эффект нелинейности компенсирует влияние «расплывания» за счет дисперсии.

В предельном случае линейного приближения после преобразования Фурье получим дисперсионное уравнение .

В нелинейной ситуации нас будет интересовать периодическое решение

. .

Уравнение Кортевега-де Вриза в такой ситуации превращается в обыкновенное дифференциальное уравнение

.

Потребуем выполнения условия

или

После интегрирования будем иметь

.

Отсюда получаем представление

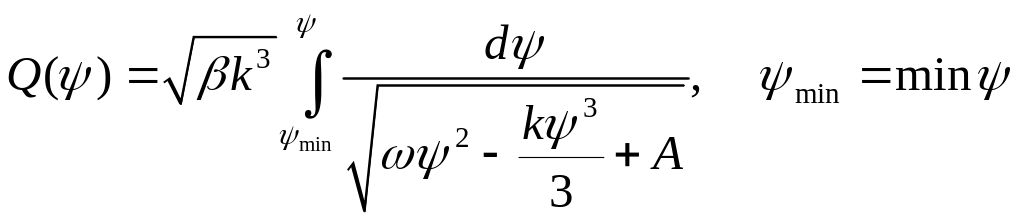
Уравнение для нахождения точек экстремума функции .

В линейном приблжении это уравнение принимает вид .

Условие периодичности функции имеет вид

.

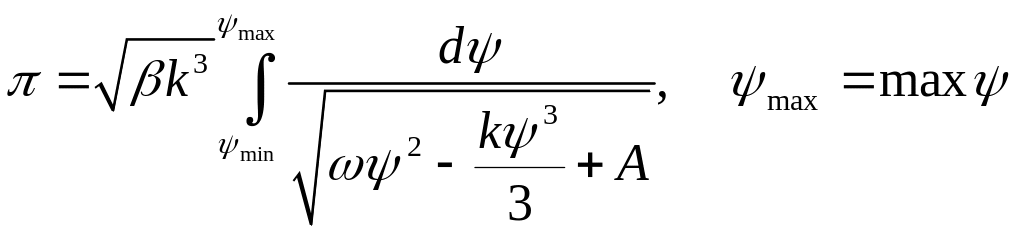Это и есть нелинейное дисперсионное уравнение, дающее связь . Здесь параметр характеризует амплитуду периодической волны. В случае линейного приближения дисперсионное уравнение не содержит амплитуды волны, оно принимает вид

,

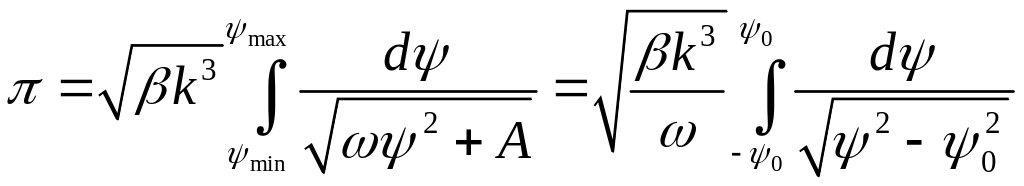. Или .

Это соотношение приводится к виду линейного дисперсионного уравнения, полученного выше на основе преобразования Фурье .

Следует обратить внимание на то, что в нелинейной ситуации понятие дисперсионное уравнение вводится только для периодических процессов. При этом частота зависит не только от волнового числа, но имеется зависимость частоты от амплитуды волны. Эта амплитуда характеризуется параметром .

10.17. Различные принципы излучения волн в средах без дисперсии и в средах с дисперсией. Особенности использования принципа излучения Зоммерфельда для сред с дисперсией. При решении задач о поле, возбуждаемом сторонними источниками в безграничной среде, возникает проблема выбора правильного решения из набора возможных независимых частных решений исходных уравнений. Наибольшие трудности возникают при решении идеализированных задач без учета потерь. Существует несколько различных способов отбора решения, соответствующего физической реальности. Условия, на которых основаны эти способы, часто называются принципами излучения. Известны: принцип Зоммерфельда, принцип Мандельштама, принцип погашения поля на бесконечности и принцип причинности. Они основаны на задании граничных условий на бесконечности для самого поля или для элементарных волн, на основе которых строится это поле, на использовании закона сохранения энергии, на задании начальных условий.

Если решение строится в виде разложения по элементарным волнам, то в соответствии с принципом Зоммерфельда разложение необходимо вести по расходящимся от источника волнам.

Л.И. Мандельштам (1947) предложил отбирать физически реализуемое решение на основе требования отвода энергии от источника. Вдали от источника поле должно состоять только из волн, которые уносят энергию на бесконечность. Мандельштам отметил, что такой отбор решений важен в средах, имеющих различные знаки групповой и фазовой скоростей вдоль некоторых направлений.

Если излучение распространяется в равновесной среде, то эта среда обладает поглощением (диссипацией), хотя оно иногда бывает и достаточно малым. Это поглощение приводит к затуханию полей при удалении от источника на бесконечность. На этом основано введение бесконечно малых потерь (для облегчения построения решения иногда вводятся некоторые «искусственные» потери) в идеализированных задачах без учета диссипации (например, задача о волнах в вакууме). В построенном таким образом решении потери затем устремляются к нулю. Введение малых потерь делает очевидным отбор правильного решения, но может значительно усложнить решение исходной задачи.

Принцип причинности требует, чтобы поле возникало в некоторой точке при выполнении условия . Это поле создается источником, включаемым в момент времени . Параметр учитывает запаздывание импульса при распространении его от источника в точку наблюдения с конечной скоростью.

Все принципы исходят из разумных (но различных) предположений. Естественно ожидать, что все эти способы, примененные к решению одной и той же задачи, должны привести к одному и тому же результату. На самом деле это так для полей в средах без дисперсии, но не всегда верно при наличии дисперсии.

1). Рассмотрим вопрос об эквивалентности различных принципов излучения в среде без дисперсии. В качестве простого примера рассмотрим вопрос о выборе правильного решения волнового уравнения для скалярного потенциала

(10.72)

где - плотность сторонних зарядов, - фазовая скорость. Этому уравнению удовлетворяют два линейно независимые решения

Смысл обозначений ясен из Рис.10.16, - радиус-вектор точки наблюдения, - радиус-вектор точки интегрирования, - расстояние от точки интегрирования до точки наблюдения. Множитель является функцией Грина уравнения (10.72) (решение, соответствующее точечному источнику), - точка наблюдения. Преобразование Фурье для функций имеет вид

, (10.73)

(10.74)

Введем новую переменную , и меняя порядок интегрирования в (10.74), получим

(10.75)

Множитель представляет собой функцию Грина для решения уравнения

.

На больших по сравнению с размерами источника расстояниях ( ) величину можно приближенно представить в виде - угол между векторами . Учитывая это, представим (10.75) в виде

Подстановка этого представления в (10.73) дает

.

Принципу Зоммерфельда удовлетворяет решение , поскольку оно представляет собой суперпозицию волн, уходящих по фазе на бесконечность. Решение является суперпозицией волн, сходящихся из бесконечности к источнику. В среде без дисперсии одинаковы фазовая, групповая скорости и они совпадают со скоростью переноса энергии. Поэтому удовлетворяет принципу Мандельштама. Покажем, что удовлетворяет принципам причинности и погашения. Возьмем представление

.

Если источник включается в момент времени то Фурье – образ источника не имеет особых точек в верхней полуплоскости комплексной плоскости . Следовательно, при условии можно замкнуть контур интегрирования по на бесконечности в верхней полуплоскости. При этом будем иметь , так как в верхней полуплоскости подынтегральная функция не имеет особых точек. Таким образом, удовлетворяет принципу причинности.

Учет влияния диссипации приводит к комплексности волнового числа, причем . В разложении (10.75) условию погашения на бесконечности удовлетворяет функция . Поэтому удовлетворяет и принципу погашения. На основе решения этой конкретной задачи, пришли к выводу, что в среде без дисперсии все принципы излучения эквивалентны. Они приводят к отбору одного и того же решения . Ниже будет показано, что этот вывод носит общий характер для сред без дисперсии.

2). Пусть поле возбуждается источником конечных размеров в сплошной однородной среде с дисперсией и пусть оно описывается линейным скалярным дифференциальным уравнением

, (10.76)

где - линейный оператор, - функция, описывающая источник. Применяя преобразование Фурье, получим алгебраическую систему уравнений для фурье – образов

При получается условие существования ненулевых решений (дисперсионное уравнение)

при .

На основе преобразования Фурье имеем интегральное представление решения, являющегося суперпозицией расходящихся на бесконечность волн (это решение соответствует для среды без дисперсии)

. (10.77)

В среде без потерь функция будет вещественной. В области прозрачности вещественными будут и корни дисперсионного уравнения Следствием этого является расположение полюсов на вещественной оси (на пути интегрирования по ). Это обстоятельство приводит к необходимости определить правило обхода этих особых точек. Воспользуемся для этого принципом причинности: . При условии контур интегрирования по частоте в (10.77) можно замкнуть на бесконечности в верхней полуплоскости . Чтобы выполнилось условие , внутри замкнутого контура не должно быть особых точек (они лежат на вещественной оси). Поэтому путь интегрирования по частоте должен обходить особые точки сверху, как показано на Рис.10.17. Условие причинности можно удовлетворить также и другим способом: если в выражении заменить на . Тогда нули уравнения сместятся с вещественной оси в нижнюю полуплоскость. Контур интегрирования, проходящий по вещественной оси , при можно замкнуть на бесконечности в верхней полуплоскости. Внутри этого контура нет особых точек, поэтому получим . Возьмем параметр малым и воспользуемся приближенным представлением

.

Применим формулу

(10.78)

где означает интеграл в смысле главного значения. В результате (10.77) представим в виде

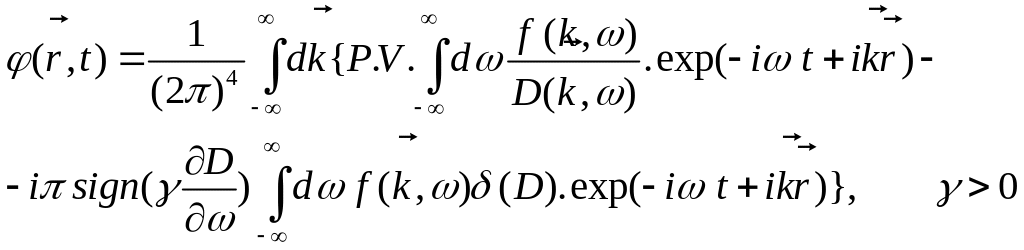. (10.79)

Это представление было получено Ю.В. Чугуновым (1969 г.), оно является решением уравнения (10.76). Это решение удовлетворяет принципу причинности.

Третий способ вычисления интеграла в (10.77) по частоте сводится к введению малой мнимой добавки в волновое число, например в составляющую волнового вектора: . Заранее знак добавки не известен. Знак должен выбираться так, чтобы потенциал удовлетворял принципу причинности. Используем приближенное представление

и применяя формулу (10.78), получим

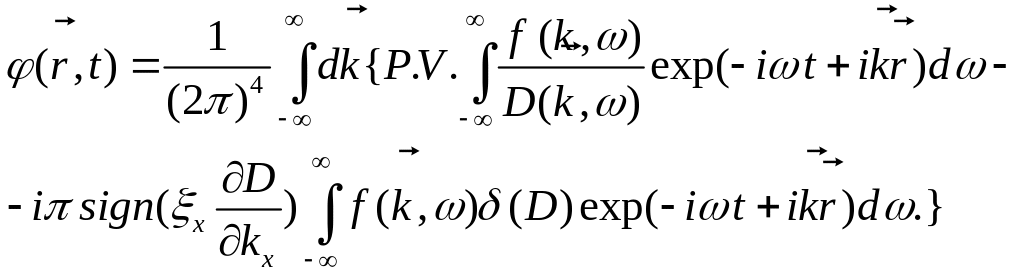. (10.80)

Первое интегрирование в (10.80) производится по . Условие совпадения формул (10.79) и (10.80) имеет вид:

.

Отсюда получаем правило выбора знака добавки

. (10.81)

Из условия получаем или . Это означает, что для компонент групповой скорости имеем представление .

Следовательно, условие (10.81) можно представит в виде .

Аналогичные рассуждения для малых мнимых добавок к компонентам приводят к правилу , (10.82.А)

Исследуем ситуацию, когда функция удовлетворяет принципу причинности.

Используя соотношения (10.82.А), выясним связь между направлением вектора (радиус – вектор между точками источника и наблюдения) и вектором групповой скорости в волнах, составляющих такое поле . С этой целью рассмотрим входящий в (10.77) интеграл

. (10.82)

При отсутствии потерь полюсы лежат на вещественной оси , а при они смещаются с вещественной оси. Замыкая контур интегрирования в (10.82) в верхней полуплоскости на бесконечности при , и в нижней полуплоскости при , имеем

1). , при ,

, при ,

2). , при ,

, при .

Таким образом, при вклад в поле дают волны, у которых выполнены условия . В области вклад в поле дают волны, обладающие свойством . В обоих случаях эти волны удовлетворяют условию . Рассматривая аналогично интегрирование по , получим следующий результат. Поле , удовлетворяющее принципу причинности, состоит из волн, для которых выполнено неравенство .

Следовательно, в этих волнах угол между векторами и должен быть острым. Именно к такому же условию приводит и принцип Мандельштама: решение должно строиться на основе волн, уносящих энергию на бесконечность, т.е. удовлетворяющих условию , где - скорость переноса энергии, или . Это соотношение получается потому, что в средах без потерь скорость переноса энергии монохроматической волны совпадает с групповой скоростью.

В то же время, в средах с дисперсией векторы и не параллельны, поэтому в таких средах одновременно могут выполняться условия и .

В таком случае использование принципа излучения Зоммерфельда приведет к выбору неправильного решения.

Можно показать (делать это здесь не будем), что решение, обладающее свойством причинности, удовлетворяет и принципу погашения поля на бесконечности. При этом имеем ограничение на : . (10.83)

Конечно, должно иметь место неравенство .

Поясним смысл этих условий. Если угол между векторами и острый, то условию затухания удовлетворяют волны, уходящие по фазе на бесконечность, в этом случае принцип Зоммерфельда справедлив. Если же угол между и тупой, то в соответствии с (10.84) затухающими на бесконечности будут волны, у которых (это волны приходящие по фазе из бесконечности). В таком случае принцип Зоммерфельда несправедлив.

10.17. Потенциалы Лиенара – Вихерта. Поле движущегося заряда. Дипольное излучение. Релятивистское излучение. Рассмотрим задачу о поле произвольно движущегося в однородной материальной среде без дисперсии точечного заряда.

1). Решение этой задачи построим, используя выражение для запаздывающих потенциалов

, , (10.84)

где - радиус – векторы точек наблюдения и интегрирования соответственно, , - время запаздывания, равное времени распространения волны от точки интегрирования до точки наблюдения, - фазовая скорость волны. Для точечного заряда , движущегося со скоростью , имеем представления

, ,

где - радиус – вектор положения точечного заряда в момент времени . Интегрирование в (10.84) осуществляется в лабораторной системе координат. Более удобно пользоваться системой координат, связанной с зарядом. С этой целью введем новую векторную переменную

и представим (10.84) в виде

, , (10.85)

где - якобиан преобразования переменных. Явный вид якобиана можно найти, воспользовавшись соотношением .

Элементы определителя находятся по формуле

,

где , . Якобиан имеет вид

.

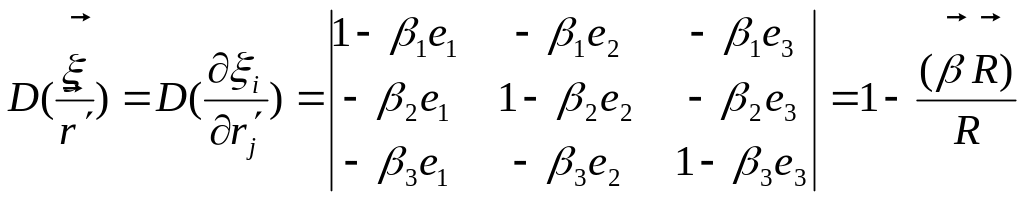После интегрирования в (10.85), получим формулы для потенциалов Лиенара - Вихерта

, , (10.86)

где , .

2). На основе представлений для потенциалов найдем электромагнитное поле, возбуждаемое движущимся зарядом:

.

Дифференцирование в этих формулах производится по и

,

где ,

, .

Из этих формул получаем

, .

Учитывая формулы Лиенара – Вихерта (10.86), получим

,

где

,

,

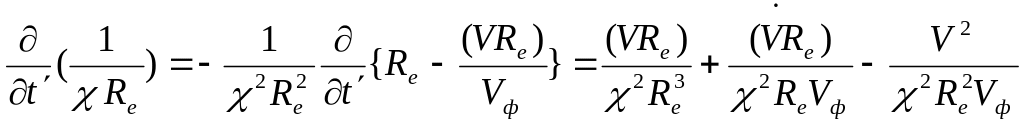после довольно громоздких преобразований получается представление для электрического и магнитного полей

.

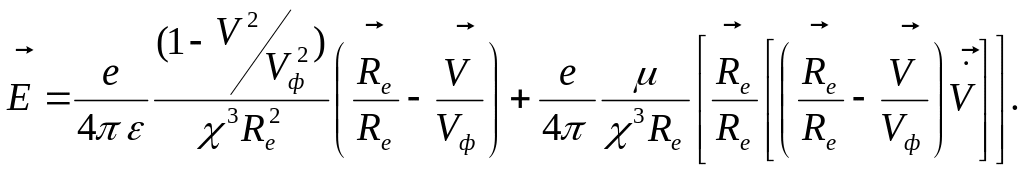
Отметим характерные закономерности для поля, движущегося точечного заряда

1). При , имеем электростатическое поле заряда: .

2). Если скорость движения постоянна, то имеет место закономерность

.

3). При в дальней зоне имеет место .

Полный поток энергии от неравномерно движущегося заряда будет отличным от нуля на бесконечности.

4). При и имеет место приближенное описание

,

В дальней зоне возможно дополнительное упрощение (дипольное излучение)

,

где - угол между векторами и . Поле имеет диаграмму направленности с максимумом при .

5). Ультрарелятивистское излучение при . Поле имеет резко выраженную зависимость от угла между векторами и (ниже этот угол обозначен ) благодаря множителю :

.

При ускоренном релятивистском движении заряженной частицы, например, при движении по окружности во внешнем магнитном поле возникает синхротронное (магнитотормозное) излучение.

6). При возникает черенковское излучение.