10.6. Фазовая и групповая скорости. Различные способы введения понятия групповой скорости. Скорость переноса энергии.

1). Понятие фазовой скорости относится к плоской монохроматической волне . Рассмотрим закономерность перемещения поверхности равной фазы .

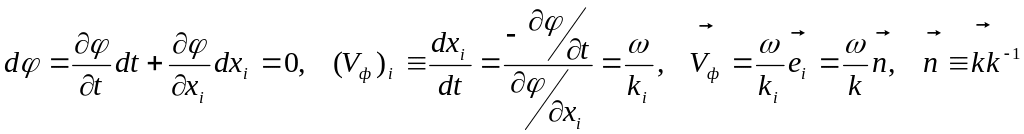
где - фазовая скорость данной плоской монохроматической волны. Так как для конкретной среды и связаны дисперсионным соотношением, то фазовая скорость является функцией частоты и волнового вектора, в общем случае эта функция может быть комплексной. Произвольное поле может быть представлено как суперпозиция плоских монохроматических волн.

Рассмотрим процесс в среде с временной дисперсией. Для простоты ограничимся случаем одномерного поля и воспользуемся представлением

. (10.9)

Где - дисперсионное алгебраическое уравнение для данной сплошной однордной среды. Это уравнение может иметь несколько корней, соответствующих различным типам волн и различным направлениям их распространения. Рассмотрим только одну волну, описываемую корнем дисперсионного уравнения . Первое интегрирование (10.9) по вычету можно проводить либо по , либо по . Сделаем первое интегрирование по и для одного типа волны получим

. (10.10)

Выясним смысл функции , для этого рассмотрим представление (10.10) в момент времени .

Согласно теореме Фурье этот интеграл можно обратить и найти

.

Эта формула определяет Фурье – образ функции .

2). Сначала рассмотрим простейший случай, когда в среде отсутствует дисперсия и в ней нет потерь (при этом ). Рассмотрение случая отсутствия дисперсии позволит выяснить простейшие идеализированные закономерности. В этом случае возможно представление (10.10) в виде

.

Здесь учтено, что при имеет место .

Первое слагаемое представляет собой некоторую функцию, зависящую от А второе – функцию от :

, .

Первое слагаемое описывает волну, распространяющуюся вдоль положительного направления оси , а второе – волну, бегущую в противоположном направлении. Обе эти волны не меняют формы в процессе своего распространения со скоростью в среде без дисперсии. Конечно, этот результат может быть получен и не прибегая к преобразованию Фурье – это следует непосредственно из волнового уравнения для поля .

3). В реальной ситуации идеализация среды без наличия дисперсии нарушается. Как уже отмечалось выше, в любом веществе в пределе диэлектрическая проницаемость стремится к проницаемости вакуума. Уже этот факт указывает на наличие временной дисперсии. Существование дисперсии это следствие общих физических принципов. Рассмотрим среду с дисперсией, но сначала ограничимся простейшим случаем суперпозиции только двух плоских монохроматических волн с близкими частотами и волновыми векторами и одинаковыми амплитудами:

,(10.11)

где причем и . Формулу (10.11) можно преобразовать к виду

.

Множитель соответствует плоской монохроматической волне со средними значениями частоты и волнового числа (в радиотехнике такая волна называется несущей). Функция описывает медленно изменяющуюся в пространстве и во времени амплитуду этой волны (огибающую). Частота изменения этой амплитуды . В результате суперпозиции двух волн близкой частоты возникает периодическое, медленное изменение амплитуды и быстрые осцилляции (биение) (Рис. 10.2). Выясним закономерности перемещения фиксированного значения амплитуды или . Так как и малы, то получаем

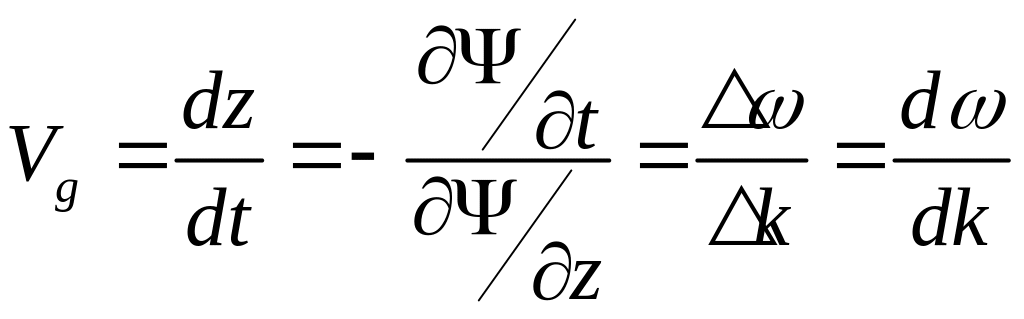
Это означает, что амплитуда биений (огибающая) перемещается со скоростью

,

которая называется групповой скоростью. Она совпадает с фазовой скоростью только при отсутствии дисперсии, когда имеется линейная зависимость от (фазовая скорость постоянна). Конечно, величине можно придать физический смысл скорости только в том случае, если эта производная вещественная (допустимо приближенное понимание групповой скорости при слабой комплексности). В случае комплексности этой производной, эволюция поля происходит более сложно, имеет место «деформация» (не происходит перемещения фиксированного вида профиля ) и это не позволяет ввести понятие огибающей и понятие скорости перемещения огибающей – групповой скорости. Иногда, чисто формально в такой ситуации групповой скоростью называют , однако эта величина не является скоростью перемещения чего-либо (возможны ситуации ).

4). Рассмотрим более общий случай квазимонохроиатической волны (волновой пакет или цуг волн), когда в суперпозиции участвуют не две волны, а непрерывная совокупность плоских монохроматических волн с узким интервалом частот и волновых векторов:

, .

Это позволяет использовать приближенное представление для (10.10)

.

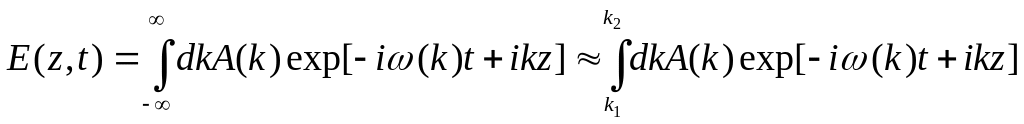Такая ситуация соответствует тому, что функция имеет резкий максимум при . Интегрирование в интервалах и дает пренебрежимо малый вклад в интеграл. Используем приближение при выполнении условия . В результате, получим ,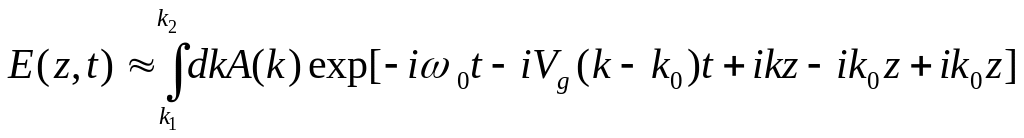

(10.12)

где ,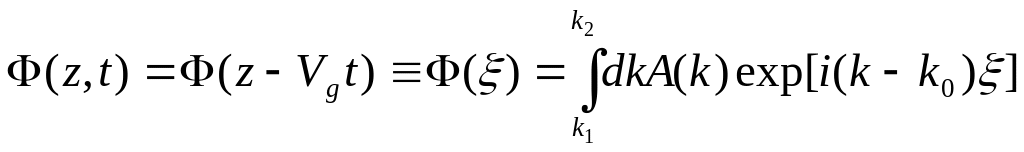

где - значение групповой скорости при , .. В случае , экспоненциальный множитель в (10.12) соответствует плоской монохроматической волне со средними значениями частоты и волнового числа . Величина описывает огибающую, которая медленно изменяется в пространстве (на расстояниях порядка ) и во времени (с временным масштабом порядка ). Огибающая – функция одного переменного . Это означает, что огибающая переносится в пространстве с постоянной скоростью, равной групповой скорости для значения . Волновой пакет (квазимонохромат) движется как единое целое, без изменения формы. Конечно, этот вывод приближенный, так как в Фурье – представлении использовались только два члена в разложении

Оценим роль отброшенного (третьего) слагаемого, приняв во внимание то, что оно умножается в показателе экспоненты на время . Условие пренебрежения имеет вид

, (10.13)

за время пакет проходит расстояние и условие (10.13) можно представить в виде - пространственный масштаб изменения волнового пакета. На расстояниях больших волновой пакет претерпевает «искажение» за счет дисперсии, он «расплывается» и здесь понятие групповой скорости теряет смысл. Выше отмечалось, что понятие групповой скорости так же теряет смысл при комплексности . Это может быть при наличии диссипации и при распространении волны в «области непрозрачности» (в этой области производная является мнимой величиной).

Под волновым пакетом понимаем суперпозицию волн с небольшим разбросом волновых векторов. Выясним, какую область в пространстве занимает такой волновой пакет. Рассмотрим простейший пример поля, сосредоточенного в пространстве в области . Сопоставим между собой величины и . Пусть имеем представление поля

,

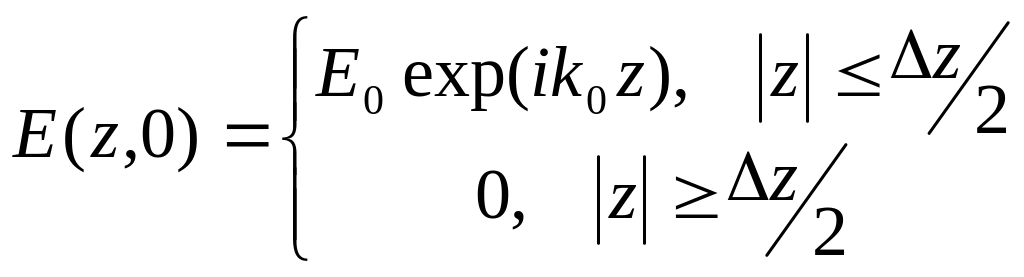при этом Фурье – образ представляется в виде

,

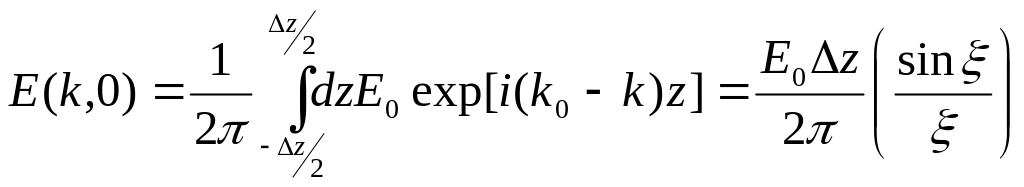где - безразмерный параметр. Функция не мала (т.е. порядка единицы) при . Ширина этого интервала составляет . Разброс волновых чисел , поэтому условие приводится к виду

.

Такое же соотношение справедливо не только для данного примера, но и для любых квазимонохроматических волновых пакетов. В трехмерных задачах будем иметь

.

Это соотношение можно представить в виде

Если обозначить интервал времени, которое пакет проводит в данной точке пространства (время прохождения пакета через данную точку), то . Справедливо представление , где - разброс по частотам в пакете. Таким образом, имеем соотношение

.

5). Найдем связь между групповой скоростью и показателем преломления ( - волновое число в вакууме). Учтем представление и продифференцируем соотношение :

откуда получим

.

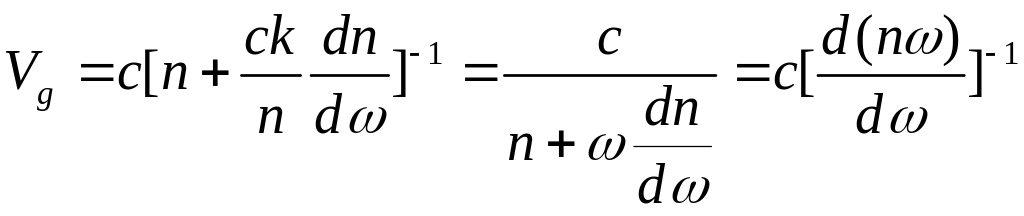В области нормальной дисперсии . Для большинства сред (но не для всех) в этой области , поэтому для них имеют место неравенства . В области аномальной дисперсии и при этом может быть очень большим. Групповая скорость в этой области может быть больше . Но это конечно, не означает, что какие то участки обгонят передний фронт, движущийся со скоростью . Эти «быстрые» участки при приближении к фронту тормозятся (при этом в окрестности фронта перестает быть применимым приближение квазимонохроматичности и теряет смысл понятие групповой скорости). Такие быстрые участки не обгоняют передний фронт. В области аномальной дисперсии групповая скорость может быть и отрицательной, при этом огибающая перемещается в сторону, противоположную той, в которую перемещается поверхность равной фазы. В таких ситуациях понятием групповой скорости нужно пользоваться с большой осторожностью. При исследовании эволюции поля нужно обратиться к исходному представлению Фурье (10.10) для волны данного типа и вычислять этот интеграл нужно по возможности наиболее точными приближенными методами (если интеграл вычисляется точно, то проблема вообще не возникнет).

6). Получим формулу Рэлея и рассмотрим геометрический способ Эренфеста получения связи групповой скорости с фазовой скоростью. При отсутствии дисперсии имеет место соотношение

.

При этом групповая скорость совпадает с фазовой скоростью:

.

Наличие дисперсии учтем, введением функции :

.

Учитывая соотношение для длины волны , получим формулу Рэлея

.

В зависимости от знака производной групповая скорость может быть как больше, так и меньше фазовой скорости . Возможно обращение в ноль и допустима ситуация . Эренфест предложил графический способ нахождения по кривой . В точке на Рис. 10.2.А пунктирная линия касается кривой . Из Рис. 10.2.А видно, что длина отрезка дается соотношением

.

Отрезок отсекаемый на оси ординат касательной к кривой в точке удовлетворяет формуле Рэлея

.

На Рис. 10.2.Б Изображены различные ситуации для случаев . Следует отметить, что в ситуациях, когда возможно нарушение применимости понятия групповой скорости, в частности: не происходит ли искажение профиля огибающей.

7). Рассмотрим еще один способ введения понятия групповой скорости. Это позволит ввести новые полезные понятия и позволит придать групповой скорости новый смысл. Пусть имеется квазимонохроматическое поле вида (ради простоты ограничиваемся случаем «одномерного» поля ):

, (10.14)

где - медленно изменяющаяся огибающая, - быстро осциллирующая, периодическая по функция. В частности, может быть использовано представление . В предельном случае монохроматического поля . Здесь - корень дисперсионного уравнения, описывающий некоторый тип волны. При этом и не зависят от переменных , в линейных полях. Значения и не зависят от амплитуды поля. В нелинейных полях и зависят от амплитуды поля. В нелинейных полях понятие нелинейного дисперсионного уравнения вводится не опираясь на преобразование Фурье. Нелинейным дисперсионным уравнением называется условие существования периодического решения.

Для квазимонохромата (10.14) по определению вводятся понятия локальная частота и локальное волновое число :

, (10.15) . (10.16)

В предельном случае монохроматической волны, определение (10.15), (10.16) дают правильный результат: , . Для локальных функций частота и волновое число можно использовать связь , существующую для монохроматической волны (имеется доказательство справедливости этого утверждения, но здесь приводить его не будем).

Продифференцируем (10.15) по , и (10.16) по . Сложение этих результатов дает уравнение, связывающее между собой локальные функции и

. (10.17)

Это очень интересный результат. Уравнение (10.17) это аналог уравнения неразрывности (закона сохранения). Локальное волновое число это аналог плотности (плотность волн), а локальная частота это поток (поток волн). Сразу возникает способ вычисления : нужно подсчитать число периодов волны на единице длины. Для нахождения нужно подсчитать число периодов волны, проходящих через данную точку за единицу времени. Если в (10.17) использовать связь и определение групповой скорости , то получим уравнение в частных производных гиперболического типа для описания эволюции локального волнового числа

. (10.18)

Следствием нелинейной связи (10.14) является то, что при решении линейной задачи получилось нелинейное уравнение гиперболического типадля локального волнового числа. Уравнение (10.18) можно привести к характеристической форме (представить в виде обыкновенного дифференциального уравнения в новой системе координат). Существуют несколько процедур для реализации этого. Однако, уравнение (10.18) очень простое и переход к характеристической форме делается, если учесть определение полной (материальной) производной по времени: , где - скорость перемещения точки наблюдения. Значит, характеристическая форма (10.18) имеет вид

(10.19) Это уравнение справедливо на линии . (10.20)

Линия (10.20) называется характеристикой. На характеристике согласно (10.19)

,

а из уравнения характеристики (10.20) следует, что характеристика – прямая линия, так как

.

Таким образом, возможно следующее определение групповой скорости: это такая скорость перемещения наблюдателя, что он в квазимонохроматической волне видит локальное волновое число постоянным (локальная частота при этом так же будет константой ).

8). Найдем теперь связь групповой скорости со скоростью переноса энергии плоской монохроматической волной в однородной изотропной среде с временной и пространственной дисперсиями, но без потерь. Для плоской монохроматической волны уравнения Максвелла записываются в виде

, (10.21) . (10.22)

Здесь - вещественная функция.

Перейдем от этих уравнений к уравнениям для приращений Дифференциалы (10.21) и (10.22) дают

,

.

Эквивалентная форма этих соотношений

, (10.23) . (10.24)

Умножим (10.23) скалярно на , а уравнение (10.24) – на . Учитывая формулу

,

Получим

, (10.25)

. (10.26)

Вычитая (10.26) из (10.25), будем иметь

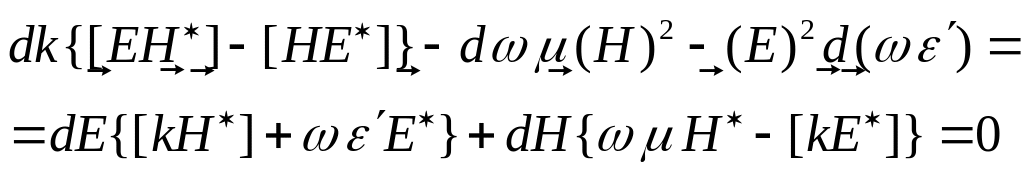(10.27)

Равенство нулю правой части это следствие уравнений (10.21), (10.22) при вещественных и в среде без потерь. Преобразуем уравнение (10.27), приняв во внимание соотношения

, . Получим (10.27) в виде

.

Здесь - средняя за период плотность энергии магнитного поля, - средняя за период плотность электрической и кинетической энергии заряженных частиц вещества, - составляющая вдоль средней за период плотности потока кинетической энергии, - средняя за период плотность потока электромагнитной энергии. Так как для групповой скорости имеем определение

,

то приходим к представлению

, .

В среде без потерь средняя за период энергия сохраняется, уравнение неразрывности имеет вид

и имеет место связь - скорость переноса энергии. Значит,

.

Таким образом, групповая скорость плоской монохроматической волны в среде без потерь совпадает со скоростью переноса энергии этой волной.

10.6-А. Свойства диэлектрической проницаемости и волнового числа.

Имеет место представление Фурье для в ситуации, когда отсутствует пространственная дисперсия

В среде без пространственной дисперсии функция обладает свойствами:

.

Исследуем зависимость от частоты параметра . Для фазовой скорости имеем представление

.

Функция связана с относительной комплексной диэлектрической проницаемостью изотропной среды формулой

.

Выше отмечалось, что любая среда для достаточно высоких частот ведет себя как вакуум. В этой области частот, пренебрегая пространственной дисперсией, воспользуемся разложением

(10.28)

В квадратных скобках формулы (10.28) отсутствует слагаемое вида . При этом в пределе имеем , . Если бы в (10.28) присутствовал член , то имело бы место представление при . Последнее представление противоречило бы закономерности при .

10.7. Распространение переднего фронта нестационарной волны. Интегральное представление одномерного нестационарной волны, распространяющейся в направлении и соответствующей одному из типов волн в однородной среде ( - корень дисперсионного уравнения ). В среде с потерями для такой волны . Особые точки функции для пассивных сред расположены в нижней полуплоскости.

, (10.29)

где функция имеет передний фронт на уровне :

.

Согласно (10.29) имеем представление

.

Особые точки подынтегральной функции в (10.29) (особые точки функций и ) лежат в нижней полуплоскости . Это обеспечивает выполнение принципа причинности (поле отсутствует до момента включения источника). Соотношение (10.29) представляется в виде

, (10.30)

,

Где называется импульсной функцией:

, (10.31)

она обладает свойством ( - дельта функция Дирака).

Покажем, что импульсная функция удовлетворяет принципу причинности. Выясним, при каких значениях аргумента импульсная функция станет отличной от нуля. При больших значениях , в области замыкания контура интегрирования на бесконечности, можно воспользоваться разложением (10.28) и будем иметь приближенное представление экспоненты

.

Подчеркнем тот факт, что это представление не будет использоваться при вычислении интеграла в (10.31), оно используется только для определения возможности или невозможности замыкания контура при .

При выполнении условия имеется возможность замкнуть контур интегрирования на бесконечности в верхней полуплоскости . Так как внутри такого контура нет особых точек, то

при , . (10.32)

Если , то можно замыкать контур интегрирования на бесконечности в нижней полуплоскости . Наличие особых точек в нижней полуплоскости обеспечивает следующее свойство

при . (10.33)

Предельное представление было использовано только для получения соотношений (10.32), (10.33)

Покажем, что передний фронт нестационарной волны движется со скоростью . Свойства (10.32), (10.33) позволяют поле представить в виде

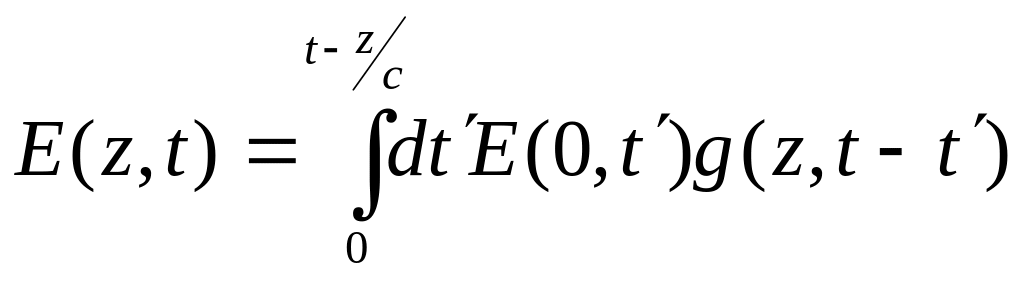. (10.34)

Поле при , так как при этом интегрирование в формуле (10.34) проходит в области отрицательных значений переменной , где по условию включения . Это соответствует тому, что волновой процесс, порожденный полем еще не достиг уровня . Поле обладает свойством причинности:

(10.35)

это свидетельство того, что передний фронт нестационарного поля в любой среде распространяется со скоростью света в вакууме. Отдельные характерные точки (нули, максимумы,…) поля могут перемещаться со скоростью большей, чем , однако они тормозятся при приближении к фронту и не могут обогнать его.

10.8. Теоремы единственности для стационарных (гармонических полей) задач. Докажем теоремы единственности решения уравнений Максвелла для комплексных амплитуд стационарных полей в неоднородных изотропных средах с потерями. Исходные уравнения для комплексных амплитуд имеют вид

(10.36) , (10.37)

где , . Существуют два типа задач: внутренние и внешние.

В случае внутренних задач по заданному стороннему току ищутся поля внутри объема (Рис. 10.3). На границе этого объема задаются условия для касательных составляющих полей

(10.38)

где поверхности и могут перекрываться. Докажем, что решение системы (10.36), (10.37) с условиями (10.38) единственно. Для этого допустим, что и два различных решения задачи. Тогда разностное решение должно удовлетворять системе (10.36), (10.37) без стороннего источника и это разностное решение удовлетворяет нулевым граничным условиям

. (10.39)

Для этого поля напишем известное энергетическое соотношение

Следствием условия (10.39) является , поэтому имеем

.

В среде с потерями это равенство выполняется только при условии , что и доказывает единственность решения внутренней задачи. В среде без потерь однозначности решения не будет, так как возможно выполнение равенства

при .

В случае внешних задач электродинамики ищется решение системы (10.36), (10.37) вне некоторых объемов (Рис.10.4), на поверхности которых задаются граничные условия

Внешнюю задачу можно свести к внутренней задаче, если ввести поверхность бесконечно большого радиуса. На поверхности задается граничное условие

которое называется условием излучения. Это условие в средах с потерями выполняется за счет экспоненциального убывания полей. Доказательство утверждения единственности внешней задачи далее проводится так же как и для внутренних задач. При решении задач в средах без потерь можно ввести малые потери, построить решение, а затем в этом решении сделать предельный переход к среде без потерь.

10.9. Отражение плоских волн от плоской границы раздела. В однородной и безграничной среде могут распространяться плоские монохроматические волны. Если среда неоднородна, то монохроматические волны в ней, вообще говоря, уже не являются плоскими. Существует важный случай, когда и в неоднородной среде могут распространяться плоские монохроматические волны. Это случай двух однородных полу - бесконечных сред, соприкасающихся вдоль плоской границы. Рассмотрим такой случай.

Плоские волны удовлетворяют уравнениям Максвелла внутри каждого из полупространств, заполненных однородной средой с параметрами и (Рис.10.5). Поэтому вопрос сводится к тому, как удовлетворить граничным условиям на поверхности раздела сред и на бесконечности. Пусть плоская волна падает на границу из среды под углом к вертикальной оси В среде возникает преломленная волна, идущая в направлении под углом к оси В среде появляется отраженная волна , которая идет в направлении под углом к оси На Рис.10.5 сплошными линиями изображена ситуация (ниже этот случай назовем ситуация №1),когда в среде компонента вектора фазовой скорости имеет тот же знак, что и компонента вектора скорости переноса энергии . В этом случае энергия переносится в область волной, уходящей в сторону . Однако существуют среды, у которых (назовем этот случай ситуацией №2). В этом случае волна, уносящая энергию в область , должна приходить по фазе из области к границе раздела сред. Эта волна на Рис.10.5 изображена пунктирными стрелочками. Подробнее об этой ситуации см. Мандельштам Л.И. «Лекции по оптике, теории относительности и квантов», 1972, стр. 394 и 435.

Плоскую электромагнитную волну можно разбить на две волны с разной поляризацией), распространяющиеся независимо друг от друга. Введем понятие плоскость падения волны как плоскость , проходящую через ось и через вектор, характеризующий направление распространения падающей плоской волны. Ось проведем в плоскости падения (ось перпендикулярна плоскости падения). Волной вертикальной поляризации назовем волну, у которой . Волна горизонтальной поляризации имеет . Коэффициенты отражения и преломления (прохождения) этих волн различаются. Рассмотрим подробно задачу о волне горизонтальной поляризации.

Электрическое поле падающей волны запишем в виде

,

где , - волновое число в первой среде, . Отраженную от границы волну опишем соотношением

,

где - коэффициент отражения волны горизонтальной поляризации, . Во второй среде будет преломленная волна

,

где - коэффициент преломления, .

На Рис.10.5 вектор для ситуаций №1 и№2 изображен соответственно сплошной и пунктирной линиями.

При написании представлений для отраженной и преломленной волн использованы соображения:

1). Поскольку падающее поле не зависит от координаты , свойства среды также не зависят от , то отраженная и преломленная волны не зависят от этой координаты.

2). Электрическое поле в падающей волне описывается вектором , параллельным границе раздела. На границе раздела составляющая непрерывна. Поэтому в отраженной и преломленной волнах вектор электрического поля сохраняет ориентацию (в анизотропных средах это не так).

3). Считается, что отраженная и преломленная волны остаются плоскими

Использование таких допущений позволяет построить решение Оно единственно согласно соответствующей теореме.

Сначала рассмотрим ситуацию №1. На границе раздела сред тангенциальная составляющая поля должна быть непрерывна:

. (10.40)

Это условие должно быть выполнено при любых значениях , а это приводит к условию равенства показателей экспонент

. (10.41)

Из (10.40), (10.41) следует соотношение

. (10.42)

Равенство (10.41) – это закон Снеллиуса. Из (10.41) следует, что . Для однозначного выбора необходимо привлечь условие убывания отраженного поля при . Это требование выполняется при . В результате получаем . На Рис.10.5 введен угол . Из закона Снеллиуса получаем представление для угла преломления

.

Если показатель преломления - вещественный и , то тогда , т.е. нормаль к поверхности равной фазы преломленной волны «прижимается» к вертикальной оси . При выполнении условия угол может быть комплексным при . Если - комплексное число, то и принимают комплексные значения. При этом , в соответствии с условием затухания преломленной волны при должно выполняться условие

Для того, чтобы найти явный вид коэффициентов нужно кроме (10.42) добавить еще одно условие. Для этого используем граничное условие

(10.43)

для тангенциальных компонент магнитного поля при отсутствии поверхностных токов. Используем уравнение

,

которое для горизонтальной поляризации имеет вид

.

Отсюда получаем представления полей падающего, отраженного и преломленного:

, ,

.

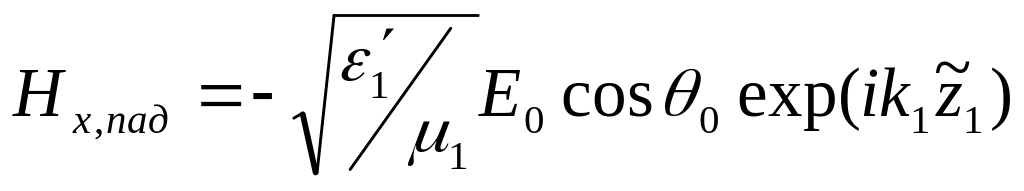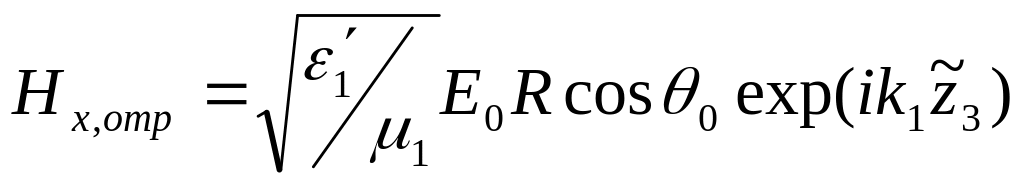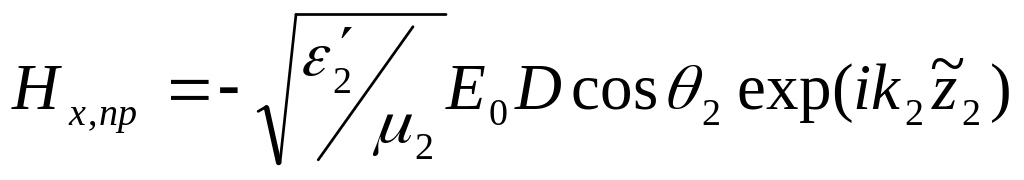Из граничного условия (10.43) получаем

,

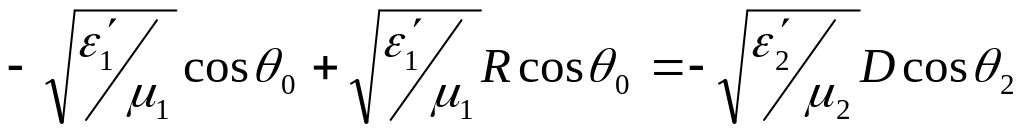которое совместно с условием (10.42) позволяет определить коэффициенты для волны горизонтальной поляризации

,

,

где 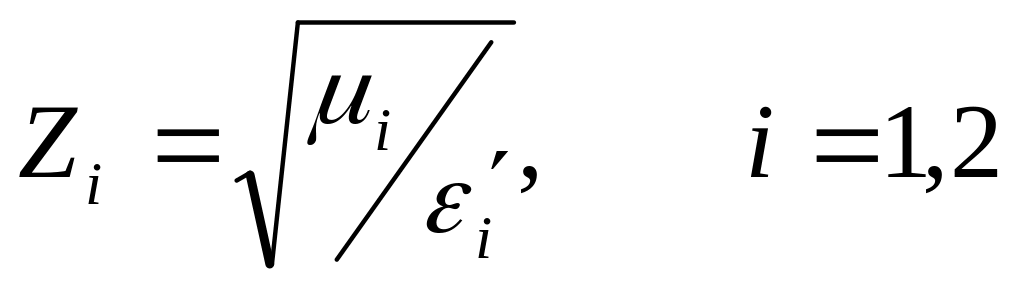. - характеристические импедансы (волновые сопротивления) сред.

В случае волны вертикальной поляризации задача решается аналогично, получается:

,

.

Рассмотрим некоторые предельные случаи для задачи о волне горизонтальной поляризации.

1. При отражении волны от оптически более плотной среды, когда выполняются условия 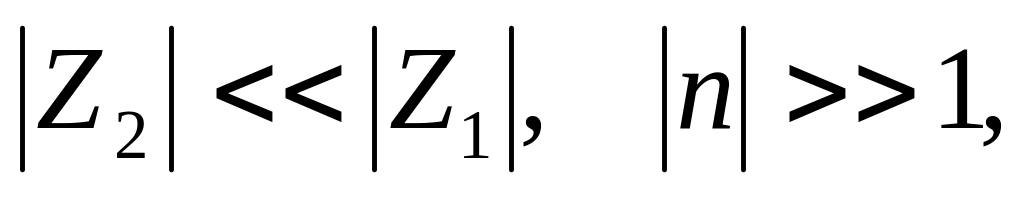получаем 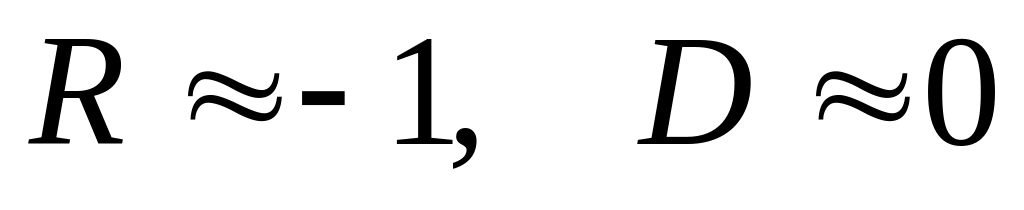. В этом случае на границе имеем «узел» напряженности электрического поля: 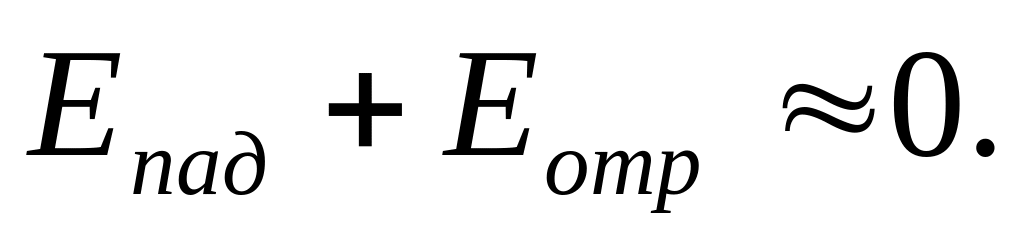Такая ситуация наблюдается при отражении от металла.

2. Отражение волны от менее плотной среды. Будем считать, что 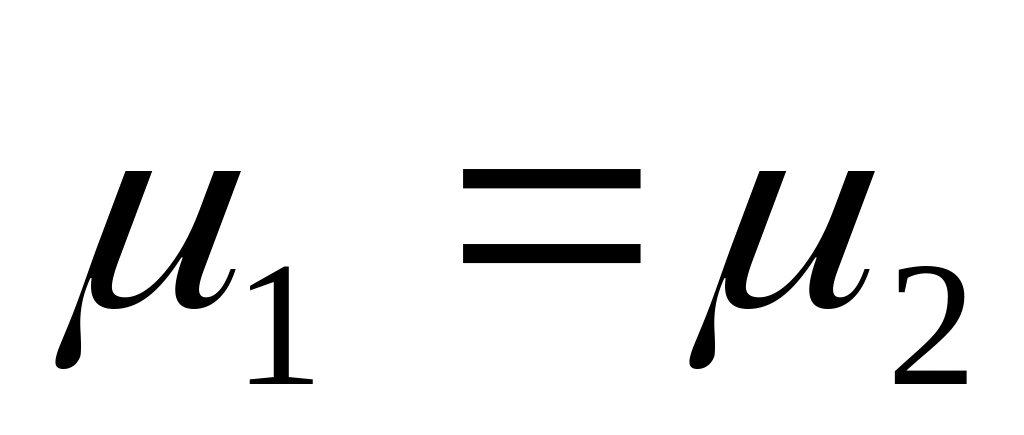, 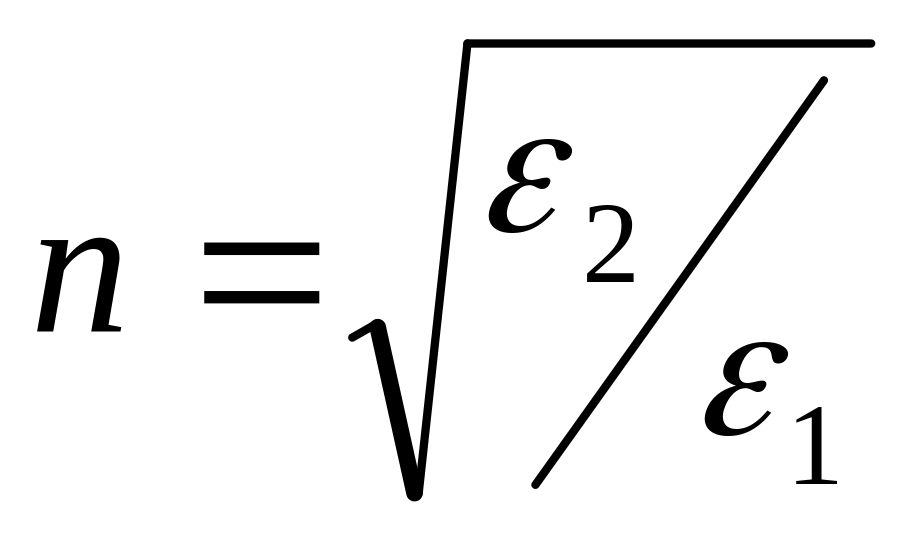<1. Из закона Снеллиуса следует, что вещественным угол будет только при выполнении условия 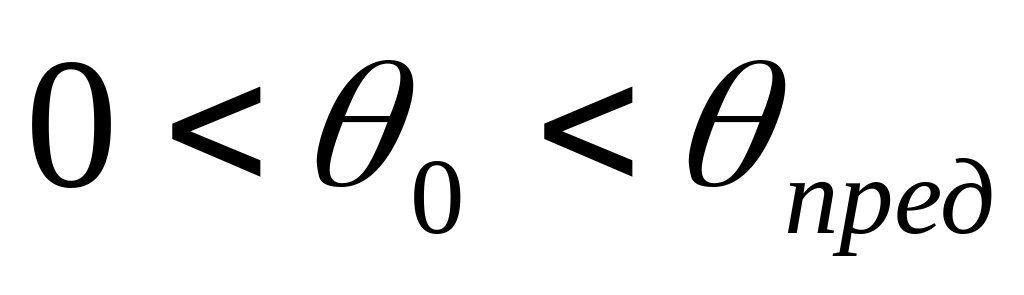, где При 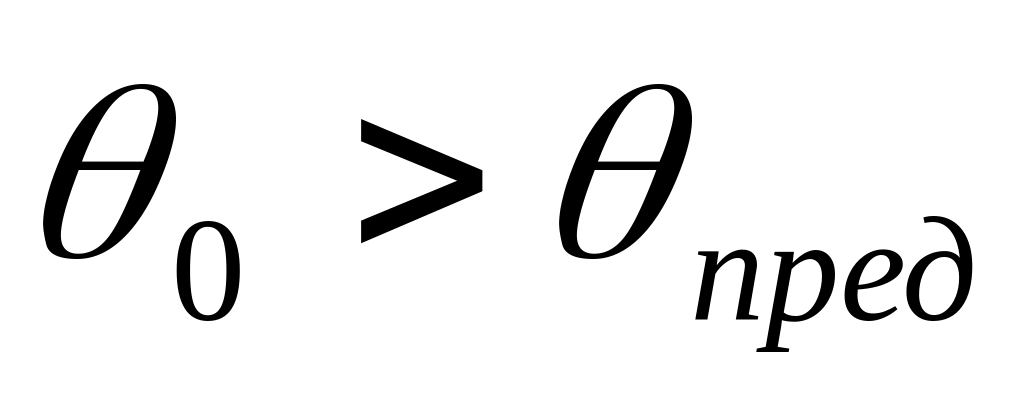наступает полное внутреннее отражение от оптически менее плотной среды. В этом случае 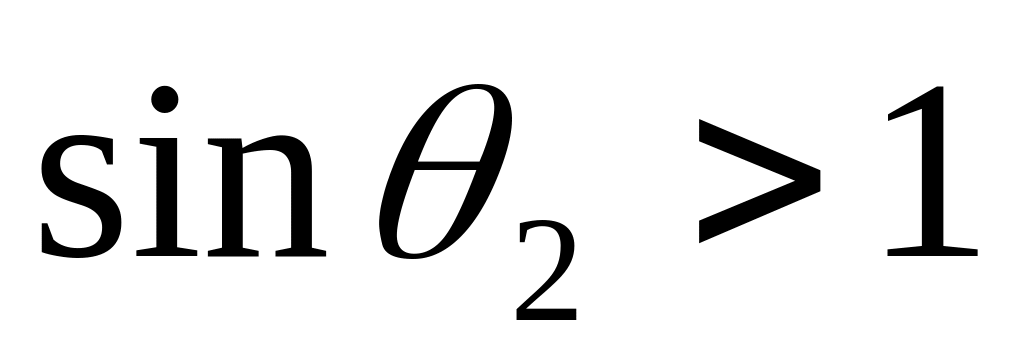, поэтому 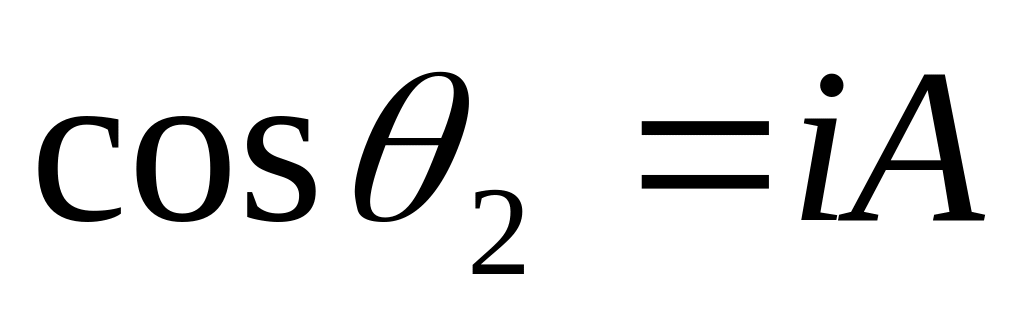- чисто мнимая величина 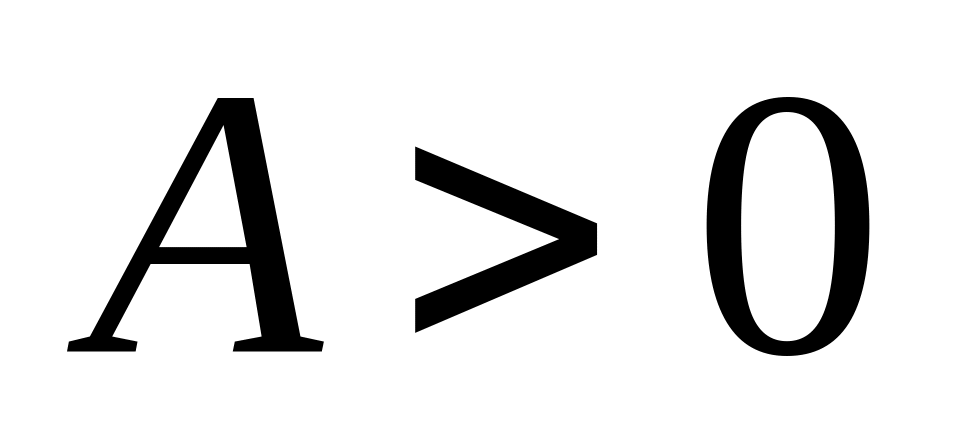. В результате преломленная волна в среде будет экспоненциально затухать при отходе от границы раздела:

Коэффициенты в такой ситуации представляются в виде

,

следовательно, при полном внутреннем отражении электрическое поле в верхней среде имеет структуру поверхностной волны: она является распространяющейся вдоль оси , а с увеличением расстояния от границы амплитуда поля экспоненциально убывает. Глубина проникновения волны в среду имеет вид

При учете представлений , получаем

При глубина проникновения , но с ростом она уменьшается.

В заключение рассмотрим вопрос о среднем за период потоке энергии во второй среде при условии полного внутреннего отражения. В преломленной волне горизонтальной поляризации имеется электрическое поле и две компоненты магнитного поля , которые найдем из уравнения . Имеем:

Получаем представления

. .

Вектор Пойнтинга имеет две компоненты: . Средний за период поток энергии определяется в виде .

Таким образом, поток энергии во второй среде при полном внутреннем отражении направлен вдоль границы (Рис.10.6) и он убывает по мере удаления от границы по закону . Так выглядит явление при отсутствии потерь во второй среде. Учет потерь приведет к тому, что . Для выяснения динамики установления такой специфической картины распределения потока энергии, необходимо решать нестационарную задачу.

Аналогично рассматривается ситуация №2, угол преломления при этом равен . Формулы для коэффициентов отражения и преломления здесь не приводим.

10.10. Приближенные граничные условия Леонтовича. Поверхностный импеданс. Для того чтобы решить задачи электродинамики при наличии границ раздела и найти поле в одной из этих сред, необходимо найти поля во всех средах, учитывая граничные условия. Имеются ситуации, когда допустимо приближенное нахождение поля с использованием приближенных граничных условий Леонтовича для искомого поля. При таком подходе задача существенно упрощается, так как определяется поле только в одной среде. Этот способ оказывается применим, если среда, в которой ищется поле, граничит с хорошо проводящей средой, имеющей большой (по абсолютной величине) показатель преломления.

Рассмотрим простейшую ситуацию: наличие плоской границы раздела между двумя полу пространствами с различными свойствами (рис.10.7). Пусть среда имеет свойства вакуума а в среде токи проводимости преобладают над токами смещения: и при этом выполнено неравенство . Для плоской волны по закону преломления Снеллиуса при следует: . Таким образом, при любом угле падения волна во второй среде идет почти перпендикулярно к границе. Для волны горизонтальной поляризации во второй среде будем иметь

Так как тангенциальные составляющие поля непрерывны на границе, то аналогичная связь должна быть и в первой среде при :

.

Проведя аналогичные рассуждения для плоской волны вертикальной поляризации, придем к граничному условию

.

Таким образом, получен приближенная связь между тангенциальными составляющими поля в первой среде на границе раздела, однако, в эту связь входят свойства второй среды – поверхностный импеданс Оба условия записываются в виде единой формы

, (10.44)

где - внешняя к первой среде единичная нормаль на границе.

Условия (10.44) являются приближенными граничными условиями Леонтовича (1948 г.) Для плоской волны точность этого условия повышается, при выполнении условия . При нормальном падении волны на плоскую границу раздела, условие Леонтовича становится точным.

Условие соответствует тому, что

.

Значит, поле во второй среде экспоненциально затухает при увеличении расстояния

.

При выполнении условия поле проникает во вторую среду на глубину скин – слоя . Неравенство обеспечивает малость угла преломления при любых углах падения .

Большое значение условий Леонтовича заключается в том, что их можно применять при решении более сложных задач электродинамики. Рассмотрим условие их применимости в некоторых из этих случаев.

1). Если вторая оптически более плотная среда неоднородна, но неоднородность ее проявляется при , то в условии (10.44) такая неоднородность не проявится существенным образом. Если неоднородность среды проявляется уже при , но свойства каждого слоя удовлетворяют условию , , то и в этом случае применимо условие Леонтовича, но с импедансом , зависящем от свойств этих слоев.

2). Фронт падающей волны не плоский, но отличие от плоской волны слабое. Рассмотрим поле точечного источника (Рис.10.8). Пусть - расстояние от источника до участка , где рассматриваются граничные условия. Если , то фронт волны почти плоский. Если дополнительно справедливо , то на участке во второй среде волна пойдет почти перпендикулярно к границе. Таким образом, на участке при амплитуда поля на границе почти постоянна и выполняются условия применимости для использования (10.44).