Часть II. Электродинамика быстропеременных процессов.

10. Описание электромагнитных волн. Волновое уравнение для процесса в однородном изотропном диэлектрике. Плоские волны. Плотность и поток электромагнитной энергии. Уравнения Максвелла для комплексных амплитуд. Диэлектрическая проницаемость при очень больших частотах. Энергетические соотношения для стационарных процессов. Энергия поля в диспергирующих средах. Фазовая и групповая скорости. Различные способы введения понятия групповой скорости. Скорость переноса энергии. Распространение переднего фронта нестационарной волны Теоремы единственности для стационарных задач. Отражение плоских волн от плоской границы раздела. Приближенные граничные условия Леонтовича. Поверхностный импеданс. Потенциалы в электродинамике. Поле точечного и пространственно распределенного источников в однородной среде без дисперсии. Поле короткой линейной антенны. Диполь Герца. Принцип перестановочной двойственности. Дисперсионное уравнение для волн в анизотропной среде. Нелинейное дисперсионное уравнение. Свойства плоских волн в однородной анизотропной среде. Различные принципы излучения волн в средах без дисперсии и в средах с дисперсией. Особенности использования принципа излучения Зоммерфельда для сред с дисперсией. Потенциалы Лиенара – Вихерта. Поле движущегося заряда. Дипольное излучение. Релятивистское излучение.

10.1. Волновое уравнение для процесса в однородном изотропном диэлектрике. Плоские волны. Плотность и поток электромагнитной энергии. Переходя к изучению электромагнитных волн в материальных средах, начнем с волн малой амплитуды (линейное приближение) в однородном изотропном диэлектрике при отсутствии сторонних зарядов и токов

, , .

Рассмотрение начнем с простейшего случая отсутствия пространственной и временной дисперсии: Используя формулу

получим волновое уравнение для электрического поля

.

Аналогичное уравнение получается и для магнитного поля

.

Эти волновые уравнения отличаются от волновых уравнений для полей в вакууме только тем, что в них вместо входит величина . Отсюда следует вывод, что электромагнитные волны распространяются в диэлектрике со скоростью . Как и в вакууме, волны являются поперечными.

Рассмотрим плоские монохроматические волны (фурье – образы полей)

.

где - комплексные константы. Волновой вектор ориентирован в направлении распространения волны. Для плоской волны справедливо

.

Волновое уравнение – однородное дифференциальное уравнение в частных производных с постоянными коэффициентами, оно для плоских волн превращается в однородное алгебраическое уравнение. Условие разрешимости последнего дает дисперсионное уравнение

.

Отсюда находим . Знаки соответствуют волнам идущим в противоположные стороны. Фазовая скорость для плоских волн определяется следующим образом: . Рассмотрим одну волну 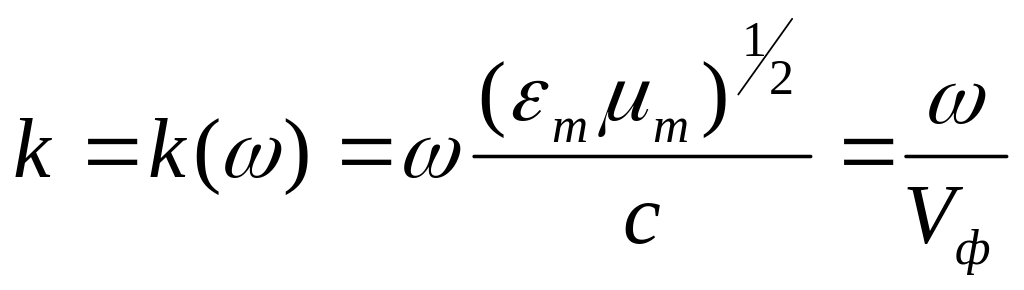. Будем иметь представление , из которого следует .

Умножив это равенство на , получим соотношение

.

Волна является поперечной. Оба поля взаимно перпендикулярны и перпендикулярны направлению распространения волны. Для поперечного поля справедливо: , значит

.

Отсюда следует равенство плотностей электрической энергии и магнитной энергии в плоской волне:

.

Вектор плотности потока электромагнитной энергии (вектор Умова - Пойнтинга) дается формулой . Для плоской волны это выражение представляется в виде

Где - плотность электромагнитной энергии это сумма плотностей энергии электрической и магнитной:

.

Значит, можно написать

.

В среде без потерь справедлив закон сохранения энергии

И при отсутствии дисперсии скорость переноса энергии совпадает с фазовой скоростью. При наличии дисперсии эти скорости различаются.

10.2. Уравнения Максвелла для комплексных амплитуд. Используем систему уравнений Максвелла в материальных средах в следующем виде

, (10.1) , (10.2) , (10.3) , (10.4) . (10.5)

В этой системе уравнений число неизвестных функций больше, чем число уравнений, система не замкнутая. Для замыкания системы необходимо добавить уравнения материальных связей, которые в случае линейной электродинамики для немагнитных однородных сред, не изменяющих свои параметры во времени, можно записать следующим образом

,

,

.

Рассмотрим свойства полей гармонически зависящих от времени

,

Здесь и - это вещественные функции. Это можно записать в другой эквивалентной форме

.

В принципе, вместо знака «-» перед можно брать знак «+», переход от одного случая к другому осуществляется операцией комплексного сопряжения. Введем обозначение для комплексной амплитуды и придем к представлению

,

функция - это Фурье-образ функции . В соответствии с этой формулой каждый входящий в (10.1) – (10.5) вектор и скалярную функцию можно записать в таком же виде. Например,

С учетом такого представления для гармонических полей и того, что , уравнение (10.1) записывается в виде

.

Поскольку это уравнение должно выполняться в любой момент времени, то приходим к уравнению для комплексных амплитуд

.

Аналогично записываются и другие уравнения:

,

, .

В однородной среде без пространственной дисперсии, в линейной электродинамике материальные уравнения для комплексных амплитуд имеют вид

,

.

С учетом этих материальных соотношений, уравнения Максвелла принимают вид

,

Или

,

где введено обозначение

,

где - тензор комплексной проницаемости среды, - тензор относительной комплексной проницаемости среды. В случае изотропной среды , где - единичный тензор.

Уравнение неразрывности приводится к виду

.

Система уравнений Максвелла для комплексных амплитуд в случае линейной электродинамики при отсутствии пространственной дисперсии имеет вид

, ,

, ,

где имеет место материальное соотношение

.

10.3. Диэлектрическая проницаемость при очень больших частотах. В пределе функция . Это очевидно из простых физических соображений: При достаточно быстром изменении поля, процессы поляризации, приводящие к установлению отличной от индукции , вообще не успевают происходить. Можно установить предельный вид функции для любых сред при больших частотах. Частота поля должна быть велика по сравнению с частотами движения всех электронов в атомах данного вещества. Электроны в такой ситуации можно считать свободными, пренебрегая их взаимодействием друг с другом и с ядрами атомов.

Скорость движения электронов мала по сравнению со скоростью света . Поэтому расстояние , проходимое электроном в течении периода волны, малы по сравнению с длиной волны . Поле волны можно считать однородным и уравнение движения, описывающее возмущение скорости взять в виде

.

Отсюда получаем связь между комплексными амплитудами

Вектор поляризации - это дипольный момент единицы объема

где - концентрация электронов (во всех атомах единичного объема). Так как справедливо

, то имеем

.

Фактическая область применимости этой формулы начинается от далекого ультрафиолета у самых легких элементов или от рентгеновских частот у более тяжелых элементов. Величина имеет размерность частоты, она называется плазменной частотой. При происходит предельный переход по закону .

В окрестности переднего фронта волны имеется резкое изменение поля, которое описывается высокими частотами. Значит, фронт распространяется в среде с диэлектрической проницаемостью вакуума. Скорость распространения переднего фронта равна скорости распространения света Отметим, что идеализация для описания нестационарных процессов не удовлетворяет условию предельного перехода

..4. . Энергетические соотношения для стационарных процессов. Под стационарными процессами, будем здесь понимать процессы, гармонически зависящие от времени. Для них задача сводится к решению уравнений Максвелла для комплексных амплитуд. После нахождения комплексных амплитуд, переход к реальным полям осуществляется по формуле

При рассмотрении энергетических соотношений приходится сталкиваться с произведением векторов поля. При этом следует иметь в виду, что

Для гармонических полей часто важны не сами квадратичные величины, а средние за период значения этих величин. Для таких средних за период квадратичных величин можно получить удобные для использования формулы, дающие представления через комплексные амплитуды.

Определим мощность, выделяемую на сопротивлении при протекании по нему гармонического тока. Ток и напряжение сдвинуты по фазе на угол

,

Здесь и - это вещественные функции. Мгновенная мощность определяется соотношением а средняя за период мощность, выделенная на сопротивлении дается формулой

где учтено, что .

Этот же результат можно получить при помощи формального приема. Запишем и в виде

, .

Не трудно показать, что

Здесь значком обозначена операция комплексного сопряжения

.

Так как вектор Умова – Пойнтинга имеет вид , то для гармонических полей среднее за период значение его выражается формулой

.

Исходя из уравнений Максвелла для комплексных амплитуд

, (10.6)

, (10.7)

получим энергетическое соотношение, в которое входило бы значение . С этой целью, считая среду изотропной, выделим вещественные и мнимые части параметров: , , и перепишем (10.7) в виде

. (10.8)

Умножая скалярно уравнение (10.6) на , а уравнение (10.8) на и вычитая одно из другого, получим

.

Учитывая, что в левой части этого уравнения стоит , проинтегрируем уравнение по объему . После этого по теореме Гаусса – Остроградского перейдем от объемного интеграла к интегралу по поверхности , охватывающей объем . В результате получим комплексное энергетическое соотношение для гармонических полей

.

После применения операции , получим

. (10.9)

Первое слагаемое здесь представляет средний за период поток энергии через площадь . Если , то энергия уходит из объема . Второе слагаемое при

соответствует магнитным и электрическим потерям энергии внутри объема на нагревание среды. В принципе, возможны случаи неравновесных (активных сред), в которых . Правая часть (10.9) - это работа сторонних сил за период на нагревание среды и на излучение электромагнитной энергии. Рассмотрим связь между векторами и между векторами . Представим

] , , .

При , имеем . С учетом представлений для комплексных амплитуд

,

получается связь между гармоническими полями

, .

Уравнениям

соответствует эллипс (Рис 10.1) на плоскости . За один период точка на этой плоскости пробегает по эллипсу. Потери энергии пропорциональны площади этого эллипса. В случае векторы и эллипс вырождается в прямую линию, магнитные потери отсутствуют. Аналогичными свойствами обладают векторы и .

10.5. Энергия поля в диспергирующих средах. Для изменения электрической и магнитной индукций и на величину и в единичном объеме необходимо затратить работу

.

В случае статических полей и в случае сред без дисперсии индукция зависит только от поля и через диэлектрическую проницаемость от температуры среды. В особом типе кристаллов (сегнетомагнетики) ситуация сложнее: зависит от трех полей . Аналогичными свойствами обладает и поле . Поэтому, при постоянной температуре является полным дифференциалом термодинамической функции (она называется плотностью свободной энергией)

.

В простейшем случае линейных полей в среде без дисперсии свободная энергия имеет вид

,

в изотропной среде происходит дополнительное упрощение

.

В входит не только энергия самого поля, но и свободная энергия вещества, связанная с полем.

Если - плотность энергии и плотность энтропии, то имеет место термодинамическое соотношение ,

где - температура, . Если и не зависят от температуры, то .

В случае переменных во времени полей и при наличии дисперсии ситуация усложняется. При этом величина не представляет собой полный дифференциал, хотя сохраняет смысл работы по изменению индукциий и (работа, совершаемая над системой). Согласно первому началу термодинамики

,

где - изменение внутренней энергии, - изменение теплоты, выделяемой в единичном объеме вещества. Следует подчеркнуть, что не является полным дифференциалом, какой либо функции. Знание не позволяет определить обе величины и порознь, так как нужно знать еще динамику вещества (это определяет энергию вещества в поле).