3.Материальные соотношения.

3.1. Материальные соотношения в электродинамике. Временная и пространственная дисперсии в линейной электродинамике.

В том случае, когда описываются поля в вакууме, система уравнений Максвелла является замкнутой: число уравнений равно числу неизвестных функций. Заданное распределение сторонних токов и зарядов позволяет однозначно найти поля и . Система уравнений линейна, поля не зависят от амплитуды источника. Скорость распространения полей постоянна и равна скорости света в вакууме

В материальных средах уравнения Максвелла не замкнуты, число уравнений меньше, чем число неизвестных функций. Сами уравнения Максвелла линейны, но дополнительные уравнения (материальные соотношения) могут быть нелинейными. Только при описании волн малой амплитуды можно пользоваться линейным приближением таких материальных соотношений, пренебрегая влиянием нелинейных эффектов. Для замыкания системы уравнений Максвелла необходимо иметь дополнительные материальные соотношения

(3.1)

В электродинамике соотношения (3.1) вводятся на основе уравнений сплошной среды (уравнений динамики). В общем случае соотношения (3.1) являются нелинейными. В данном курсе лекций рассмотрение будет ограничено в основном линейным приближением (приближение линейной электродинамики), хотя ряд задач будет рассмотрен с учетом нелинейности. Вектор намагничивания и вектор поляризации связаны с полями линейными соотношениями

Для материальных сред, за исключением ферромагнетиков и ферритов, допустимо пренебрежение влиянием вектора намагничивания: .

Самый общий вид связи между полями и в линейной электродинамике имеет интегральный характер, учитывающий суперпозицию всех временных (до момента наблюдения ) и пространственных влияний поля на поле в точке наблюдения в момент времени

, (3.2)

где - тензор, учитывающий анизотропные свойства среды. Если среда изотропная, то компоненты тензора имеют вид , где - символ Кронекера, - скалярная функция. Отсутствие интегрирования в (3.2) в области учитывает принцип причинности: будущее не оказывает влияние на настоящее. Интегрирование по пространственным переменным учитывает то, что на индукцию в точке влияет распределение поля во всем пространстве и свойства среды во всем пространстве. Такое свойство материальной среды называется пространственной дисперсией, этот термин введен М.Е. Герценштейном в 1952 г. Одной из возможных причин пространственной дисперсии является процесс хаотического, теплового переноса заряженных частиц и наводимых ими полей из удаленных точек пространства в окрестность точки наблюдения

Получим условие слабого проявления пространственной дисперсии. Если - тепловая скорость заряженных частиц, временной масштаб изменения поля во времени , среднее расстояние проходимое этими частицами за это время оценивается в виде . Фурье - образы поля имеют вид . Пусть поле распространяется с фазовой скоростью . Тепловое движение зарядов будет приводить к изменению фазового набега волны за период на величину , где - волновое число. Влияние пространственной дисперсии за счет теплового движения зарядов среды будет пренебрежимо мало при условии малости фазового набега:

Если среда пространственно однородна, то имеет место влияние свойств среды в зависимости от расстояния точки интегрирования до точки наблюдения : При этом имеем . Если пространственная дисперсия слабая, то компоненты тензора имеют резкий максимум в окрестности точки наблюдения . Предельная ситуация отсутствия пространственной дисперсии соответствует - образной зависимости: , в этом случае имеет место свойство пространственной локальной связи векторов и :

,

поле зависит от поля и зависит от свойств среды только в точке наблюдения .

Интегрирование в (3.2) по времени от значения до момента наблюдения , учитывает влияние на индукцию всего предшествующего распределения во времени поля . Это интегрирование учитывает свойства материальной среды на промежутке времени от до . Такое свойство среды называется временной дисперсией (иногда это свойство называют частотной дисперсией). Если свойства среды неизменны (однородны, стационарны) во времени, то компоненты тензора зависят только от . Отсутствие временной дисперсии соответствует представлению . Одновременное отсутствие и временной и пространственной дисперсии приводит к локальной связи .

3.2. Материальные соотношения для гармонических составляющих плоских волн и в однородных стационарных средах. При решении уравнений в частных производных с постоянными коэффициентами удобно использовать интегральное преобразование Фурье по времени и по координатам. Это позволяет свести проблему к решению алгебраических уравнений с последующим обратным преобразованием Фурье. Если поля гармонические, то использование преобразования Фурье позволяет проводить алгебраическое исследование комплексных Фурье – образов полей. Вещественная (или мнимая) часть этих образов описывает реальные гармонические поля. Преобразование Фурье для вектора электрической индукции имеет вид

, (3.3)

где - комплексный Фурье – образ вещественной функции . Отметим, что иногда в преобразовании Фурье используется другое представление экспоненты: . Переход от функции к Фурье – образу делается следующим образом

. (3.4)

Будем интересоваться нестационарным процессом, возникающим при включении источника в момент времени . По принципу причинности поля отсутствуют при и преобразование (3.4) принимает вид

. (3.5)

Подставляя в (3.5) представление (3.2) для функции в случае однородной стационарной среды, получим

.

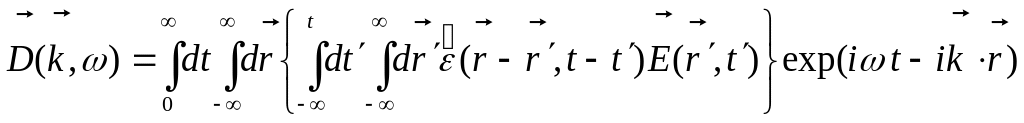Введем обозначения и получим представление

.

Поменяем порядок интегрирования и получим выражение для Фурье – образа

Выражение в фигурных скобках представляет собой , а выражение в квадратных скобках это . Таким образом, получено материальное соотношение для Фурье - образов

. (3.6)

Зависимость от частоты отражает наличие временной (частотной) дисперсии, а зависимость от волнового вектора это признак пространственной дисперсии.

В линейной электродинамике можно ввести в рассмотрение материальные связи, описывающие плотности токов

,

.

В случае однородной стационарной среды получаются соотношения для Фурье – образов

,

.

3.3 Энергетические соотношения для электромагнитного поля. Уравнения Максвелла, как уже отмечалось выше, это основные постулаты электродинамики материальных сред. Важным следствием этих уравнений является закон, описывающий баланс энергии в среде при наличии электромагнитного поля. Получим его для простейшего случая неоднородной изотропной среды без временной и пространственной дисперсии, когда справедливы соотношения

,

где - скалярная функция, описывающая диэлектрическую проницаемость неоднородной среды. Первое уравнение Максвелла

скалярно умножим на . Второе уравнение Максвелла

скалярно умножим на и вычтем одно из другого

. (3.7)

Используя формулу

,

проинтегрируем соотношение (5.1) по объему , включающему сторонние источники. Если объем не зависит от времени , то получим

. (3.8)

Воспользовавшись формулой Гаусса-Остроградского, преобразуем (3.8) к виду

, (3.9)

Где - поверхность, охватывающая объем , - внешняя по отношению к объему нормаль, - объем, в котором расположены сторонние источники. Соотношение (3.9) содержит квадратичные функции, оно выражает закон сохранения энергии в изотропной среде без дисперсии. Подынтегральное выражение во втором слагаемом

представляет собой распределенную в пространстве плотность электромагнитной энергии. Оно показывает, что всюду, где есть поля , есть и энергия.

Плотность потока электромагнитной энергии входит в подынтегральное выражение первого члена в (3.9). Слагаемое - отражает потери на джоулево тепло. Интеграл характеризует мощность стороннего источника, которую нужно затратить в объеме , чтобы электрическая и магнитная индукции изменялись со скоростями и .

Формула (3.9) приводится к виду

.

При учете дисперсии энергетическое соотношение усложняется, в него будет входить еще энергия среды (кинетическая энергия заряженных частиц). Учет анизотропии приводит к дополнительному усложнению.