9. Квазистационарные явления.

9.1. Квазистационарные явления в электродинамике. Потенциалы, описывающие квазистационарные поля. Задачи электродинамики в сплошных материальных средах описываются замкнутой системой уравнений: уравнениями Максвелла совместно с уравнениями материальных связей. Для описания непрерывных полей используются дифференциальные уравнения в частных производных Система уравнений Максвелла это линейная система. Возможно использование этой системы в различных формах, например, для неизвестных функций :

, (9.1)

, (9.2)

, (9.3)

, (9.4)

. (9.5)

Сейчас будем использовать материальные соотношения в простейшем виде. Считаем, что они представляют собой линейные локальные связи (сделано пренебрежение влиянием пространственной и временной дисперсиями)

.

В предыдущих разделах анализировались свойства статических полей, не зависящих от времени. Учет зависимости от времени приводит к значительному усложнению решения задач электродинамики. Однако, имеется круг проблем, когда допустимо использовать приближенный учет влияния зависимости полей от времени. Одно из таких приближений (квазистационарное приближение) основано на пренебрежении зависимостью вектора индукции от времени в уравнении (9.2) . Это приближение основано на пренебрежении токами смещения по сравнению с токами проводимости

. (9.6)

Для гармонического поля условие (9.6) с учетом приведенных простейших материальных соотношений запишется в виде ограничения на частоту сверху

. (9.7)

В том случае, если поля не гармонические, то в условии (9.7) следует заменить на , где - характерный временной масштаб изменения полей во времени. Приведем оценку частот, удовлетворяющих условию (9.7) для почв и для металлов. Для почв , для меди , относительная диэлектрическая проницаемость их , так что . Условие (9.7) дает ограничения

для почв,

для меди.

Как будет видно из дальнейшего исследования, квазистационарное приближение соответствует пренебрежению эффектом запаздывания при распространении электромагнитных волн в среде.

Ниже ограничимся случаем , и будем иметь квазистационарное описание полей

, (9.8)

, (9.9)

, (9.10)

, (9.11)

Равенство (9.10) позволяет ввести векторный потенциал

. (9.12)

Из уравнения (9.8) получаем представление для электрического поля

,

где произвольная функция.

Уравнение (9.11) приводится к виду

, . (9.13)

Потенциал произвольный, его выберем так, чтобы имело место уравнение электростатики

Согласно (9.13), это порождает калибровку Кулона:

. (9.14)

Уравнение (9.9) при учете представления , принимает вид . (9.15)

Это соотношение дает связь между двумя неизвестными функциями и .

Рассмотрим частный случай описания квазистационарного процесса в ситуации: :

,

так как то при имеем при . Из уравнения

следует , т.е. свободные и сторонние заряды компенсируют друг друга. Из уравнения непрерывности при следует: не зависит от времени. Так как , значит и не зависит от времени в такой ситуации. Получим теперь уравнение для поля . Для этого применим операцию к уравнению и учтем, что и имеет место представление

.

В последнем соотношении учтено, что при . В результате получим уравнение параболического типа

, при . (9.15.А)

Уравнение такого вида описывает явление теплопроводности и диффузии, параметр называется магнитной вязкостью. Ниже будет показано, что это уравнение не описывает эффекта запаздывания. Обсудим этот вопрос. Пусть - размер системы, в которой протекает процесс, - длина волны или характерный пространственный масштаб изменения полей, , где - скорость распространения волны в среде. Пренебрежение запаздыванием волны в системе возможно при условии :

или ,

где - время прохождения волны через систему, - временной масштаб изменения поля.

Для того, чтобы выяснить основные закономерности диффузии электрического поля, решим задачу на основе уравнения (9.15,А) в идеализированной постановке (раздел 9.3). При построении решения оказывается полезным знание - теоремы теории размерности.

9.2. - теорема теории размерности. Пусть имеется некоторая зависимость, определяющая размерную величину в виде функции от размерных параметров :

.

Если эта зависимость имеет физическое содержание, то она должна отражать следующий бесспорный факт. Если определяющие параметры заданы в определенной системе единиц измерения, то физическая закономерность , не зависит от произвола при выборе системы единиц измерения. Отсюда следуют интересные закономерности. Разобьем величины на две группы. В первую группу включим только определяющие параметры с независимыми размерностями (например, длина, время и т.д.). Во вторую группу будут входить параметры, размерности которых можно выразить через размерности величин первой группы. Таким образом, например, размерность параметра имеет вид размерности произведения параметров первой группы

.

Размерность величины и соответственно размерность функции имеют вид

.

Степени получаются простым подсчетом. Величины

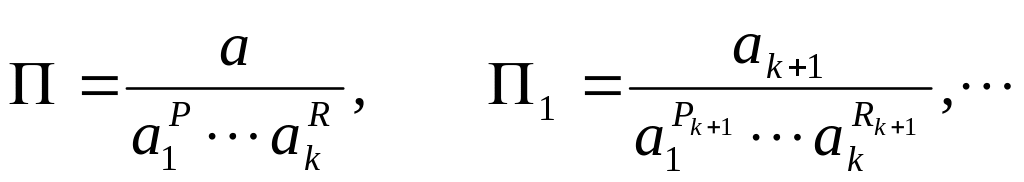
оказываются безразмерными. Поэтому значения этих величин не зависят от выбора системы единиц измерения. Независимость закономерности, имеющей физический смысл, от выбора единиц измерения означает, что соответствующее соотношение можно представить в виде (это и есть - теорема теории размерности):

,

где - безразмерная функция. У этой функции число аргументов на меньше, чем у функции . - теорема явно сформулирована и доказана Э. Бакингамом, хотя ее неявное использование началось задолго до этого (Фурье, Максвелл, Рейнольдс, Релей) Рассмотрим два простых примера.

Пример №1 – закон Кулона. Рассмотрим задачу о нахождении потенциала электростатического поля точечного заряда, находящегося в начале сферической системы координат

.

Необходимость введения связана с наличием сингулярности в начале координат у плотности заряда в случае .

Потенциал зависит от определяющих параметров :

.

В этой задаче для определяющих параметров справедливо: . Функция - безразмерная, величины имеют независимые размерности. Из уравнения

получается соответствие по размерности:

Здесь значок обозначает одинаковость размерности. Согласно - теореме имеем

.

Константа находится при подстановке этого представления в неоднородное уравнение Кулона , ,

Учет интегрирования по сферической поверхности , окружающей объем приводит к результату:

Здесь учтено, что на поверхности , где .

.

В результате получаем закон Кулона

.

Пример №2. Теорема Пифагора. Прямоугольный треугольник целиком и полностью определяется заданием острого угла и величины гипотенузы . Значит, для площади имеем представление

.

Опустим перпендикуляр из вершины прямого угла на гипотенузу. При этом основной треугольник разбивается на два подобных ему прямоугольных треугольника: один с площадью , гипотенузой , острым углом и второй с площадью , гипотенузой , острым углом ( и это катеты основного треугольника). Площади связаны соотношением . Согласно - теореме имеем

.

В результате получаем теорему Пифагора

.

Это доказательство приведено в книге А.Б. Мигдал «Качественные методы в квантовой теории» М. Наука 1975, с. 9-10. Однако, имеется утверждение, что А. Эйнштейн сделал это раньше - в возрасте 11 лет (М. Шредер «Фракталы, хаос, степенные законы», Москва-Ижевск, Регулярная и хаотическая динамика, 2005, стр.25-26)

Соображения анализа размерностей могут дать содержательный результат. Важнейшим элементом является определение совокупности определяющих параметров. Эта совокупность находится просто, если имеется математическая постановка задачи. В этом случае определяющие параметры - это множество независимых переменных и параметров, входящих в уравнения, граничные, начальные и иные условия, определяющие единственное решение. Правильный выбор определяющих параметров в задаче, не имеющей явной математической формулировки, связан с интуицией исследователя. Успех в этом случае зависит от правильного понимания того, какие параметры важны, а какими параметрами можно пренебречь.

9.3. Диффузия электрического поля. Отсутствие эффекта запаздывания в квазистационарых полях. Рассмотрим решение следующей задачи о диффузии электрического поля. Эволюцию поля опишем уравнением

, , .

Пусть в начальный момент времени задано условие

.

Электрическое поле зависит от четырех определяющих параметров

.

Первые три определяющих параметра имеют независимые размерности, а четвертый параметр позволяет составить безразмерную величину

.

Согласно - теореме поле будем искать в виде

,

где - безразмерная функция. Уравнение в частных производных для поля приводится к обыкновенному дифференциальному уравнению

.

введем вспомогательную функцию , удовлетворяющую уравнению

.

Решение этого уравнения имеет вид .

Из определения получим

,

или

,

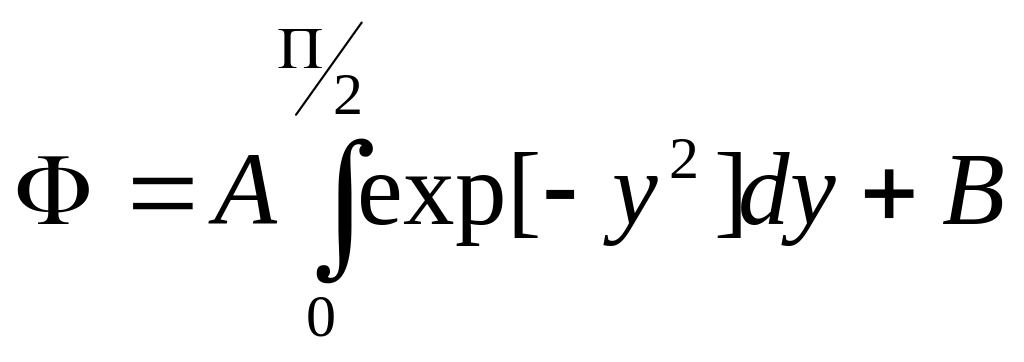где - произвольные константы, которые находятся из начального условия

.

При , имеем ,

при , имеем ,

где учтено . В результате имеем . Получаем представление

.

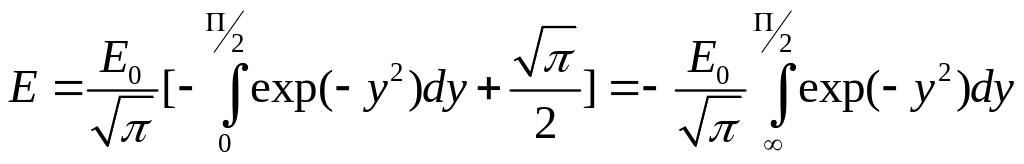Согласно этому представлению при - отсутствует эффект запаздывания (возмущения распространяются с бесконечной скоростью). Рассмотрим закономерности перемещения поверхности равной фазы , из которого получаем формулу для фазовой скорости - она конечна, и убывает с увеличением времени. Учет нелинейности может привести к формированию разрывного поля. Фронт его перемещается с конечной скоростью (реализуется эффект запаздывания).