45.Відстань від точки до прямої.

Нехай є точка та пряма Ах+Ву+С=0. Під відстанню від точки М до прямої розуміється довжина перпендикуляру , проведеного з точки М до прямої.

Для визначення відстані необхідно:

1.Сласти рівняння прямої, перпендикулярної до даної та яка проходить через точку ;

2.Знайти точку перетину двох прямих, розв’язавши систему складену з рівнянь цих прямих;

3.За формулою знайти відстань між двома точками. .

47.Загальне рівняння лінії другого порядку. Рівняння кола.

Загальне рівняння лінії другого порядку:

Загальне рівняння кола: , рівняння кола:

48.Еліпс, рівняння еліпсу та характеристична властивість.

Крива другого порядку Ax²+Cy²=δ має назву кривої еліптичного типу, якщо коефіцієнти А та С мають однакові знаки. Будемо вважати, наприклад, що А>0, С>0 тоді, можливі випадки: δ>0,δ=0,δ<0.Зрозуміло, що в третьому випадку δ<0 крива не має дійсних точок, у другому δ=0: Ax²+Cy²=0, тоді коли х=у=0, тобто рівняння визначає тільки одну точку; у третьому: δ>0- з цього випливає канонічне рів-ня еліпса:x²/a²+y²/b²=1 в якому a=√δ/A- велика напіввісь еліпса;b=√δ/C- мала напіввісь еліпса. Точки F₁(с; 0) та F₂(-с; 0),де с = √а² - Ь² мають назву фокуси еліпса, а відношення ε=c/a -ексцентриситет еліпса. Ексцентриситет характеризує форму еліпса. Зрозуміло, що 0≤ε≤1, причому для кола ε=0 (а=Ь). Точки А₁(а; 0),А_г(-а; 0), B₁(0; Ь),B₂(0; -Ь) – вершини еліпса. Суму відстаней від будь-якої точки еліпса М(х;у) до його фокусів:d=xε+a-xε+a=2a. Висновок: Для будь-якої точки еліпса сума відстаней від цієї точки до фокусів є величина стала, яка дорівнює 2а (характеристична властивість)

49.Гіпербола, її рівняння. Асимптоти гіперболи.

Крива другого порядку Ах²+Су²=δ називається гіперболою (кривою гіпербічного типу), якщо коефіцієнти А та С мають протилежні знаки, тобто А*С<0. Нехай А>0, С<0. Можливі три випадки:δ>0;2) δ=0; 3)δ<0. У першому випадку маємо гіперболу, канонічне рівняння якої x²/a² -y²/b²=1,де а=√δ/A - дійсна напіввісь; b=√δ/-C - уявна напіввісь. Фокуси гіперболи: точки F₁(с; 0),F₂(-c; 0), де

с =√a²+b², ексцентриситет: ε=a/c— приймає будь-яке значення більше 1. Вершини гіперболи: точки A₁(а; 0) та A₂(-a; 0).

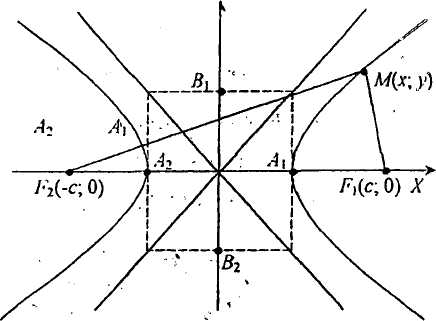
Рівняння асимптот гіперболи.

Рівняння асимптот гіперболи. Запишемо рівняння гіперболи у вигляді у=±b/a√x² - а² . Якщо х→∞, тоді √x² - а² →√x²→x,тоді останнє рівняння матиме вигляд: y≈±b/a*х, тобто при x→∞ гілки гіперболи як завгодно близько підходять до прямих y=± b/a*х, які мають назву асимптот гіперболи. Якщо а=b, маємо рівнобічну гіперболу х²-у² =а², асимптоти якої y=±x,взаємно перпендикулярні та є бісектрисами координатних кутів. У другому випадку (δ=0) рівняння Ах²+Су²=δ має вигляд x²/a² -y²/b²=0, тобто отримуємо пару прямих, що перетинаються :х/а+у/b=0 та х/а-у/b=0.У третьому випадку (δ<0) маємо криву Ах²+ Су²=δ=> x²/a² -y²/b²=-1 з піввісями а=√δ/-А,b=√δ/C, яка має назву спряженої з гіперболою x²/a² -y²/b²=1.

50. Парабола, її рів-ня та характеристична властивість. (у-y₀)²⁼2р(х-x_о) –рів-ня парaболи. Точка О'(х_о;у₀) - вершина параболи, р - параметр параболи. Якщо р>0 — гілки параболи спрямовані вправо, якщоp<0-гілки параболи спрямовані вліво. Пряма y=y₀ - вісь симетрії пара- боли. Якщо вершина параболи знаходиться на початку коо- рдинат, то рів-ня (y-y₀)²=2p(x-x₀) приймає вигляд y²=2рх. Точка F (Р/2;0) - фокус параболи, пряма х=-P/2 –директри- са. Для будь-якої точки параболи Аf(х;у) відстань до фокуса F(P/2;0) дорівнює:p(M;F)=√(x+P/2)². Оскільки x+p/2≥ 0,з іншого боку, відстань до директриси MN=x+P/2.Висновок: Параболою є множина точок площини, рівновіддалені від даної точки (фокуса) та від даної прямої (директриси) - характеристична властивість параболи.

52.Рів-ня площини, що проходить через точку перпендикулярну вектору.

Відомо, що площина проходить через т M₁(x₁; y₁; z₁) і перпендикулярно n=(A; B; C). Цей вектор називається нормальним вектором площини (вектор нормалі). Візь- мемо на площині т M(x; y; z) а потім побудуємо вектор М₁М=(x-x₁; y-y₁; z-z₁) вектори М₁М і n взаємно перпен -дикулярні  A(x-x₁)+B(y-y₁)+C(z-z₁)=0 р-ня прямої, що проходить через дану точку перпенд вектору

53.Загальне р-ня площини у просторі та його досліджнння. Загальне рів-ня площини та його дослідження. Теорема 1: У просторі R² будь-яка площина виражається рів-ням першого ступеню: Ах+Ву+Сz+D=О - загальне рівняння площини. З іншого боку, ми отримали, що площина може буди задана рівнянням:A(x-x₀)+B(y-y₀)C(z-z₀).Виконаємо деякі перетворення: Aх+Ву+Сz-Aх₀-By₀-Cz₀=0, нехай D=-Ах₀-Ву₀-Сz₀ тобто отримаємо загальне рів-ня площи- ни. Теорема 2: Будь-яке рівняння з трьома невідомими Ах+Ву+Сz+D=О визначає площину у просторі R²,якщо хоча б один з коефіцієнтів біля змінних не дорівнює ну- лю. Частинні випадки рівняння площини. 1)D=0, Ах+Ву+Сz=О - площина проходить через початок коор- динат;2)А=О, Bу+Сz+D=0-площина || осі ОХ; В=О,Ах+Сz+D=0 - площина ||осі ОУ;С=0, Ах+Ву+D=0 - площина ||осі 0Z;3)A=D=0, Ву+Сz=О - площина проходить через вісь ОХ;B=D=0, Аx+Сz=О - площина проходить через вісь ОУ;С=D=0,Ах+Ву=0 - площина проходить через ві сь 0Z;4)A=B=0, Сz+D=0 - площина || площині ХОУ;А =С=0, Ву+D=0 - площина ||площині ХОZ;B=С=0, Ах+D=0 - площина || площині У0Z;5)А =В=D=0, Сz=0, z=0 - рівняння координатної площини ХОУ;А=С=D=0, Ву=0;у=0- площина ХОZ;B=С=D=0, Ах=0, x=О - площина УОZ.

54.Взаємне роміщення площин.Умова паралельності двох площин має вигляд: А₁/А₂=В₁/В₂=С₁/С₂.Якщо крім коефіцієнтів біля змінних пропорційні й вільні члени, тобто виконується, А₁/А₂=В₁/В₂=С₁/С₂=D₁=D_2,то площи- ни співпадають.Умова перпендикулярності має вигляд: А₁А₂+В₁В₂+С₁С₂=0.