95.Означення диференціалу функції та його геометричний зміст

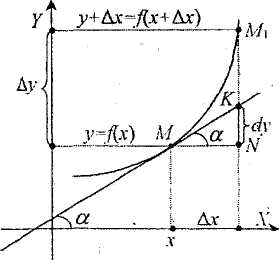
Означення: Диференціалом ф-ції називається головна, лінійна відносно ∆x частина приросту фу-ції, яка дорівнює добутку похідної на приріст незалежної змінної: dy=f'(x)∆x. Геометричний зміст диференціала. Візьмемо на графіку ф-ції y=f(x) довільну точку М(х, у). Надимо аргументу х при- ріст ∆х. Тоді функція y=y(x) отримає приріст ∆y=f(x+∆x)-f(x).Проведемо дотичну до кривої у=f(х) у точці М, яка ут- ворює кут α з додатнім напрямком осі Ох, тоді f'(x)=tgα. З прямокутного трикутника MKN:KN=MN*tgα=∆x*tgα=f ' (x)∆x, зідно з dy= f ' (x)∆x, маємо dy=KN.

Таким чином, диференціал ф-ції - є приріст ординати дотич- ної, проведеної до графіка ф-ції у=f(x) у даній точці, коли х отримує приріст ∆х.

96.Інваріантність форми диференціалу. Розглянемо ф-цію y=f(u), де аргумент и=φ(х) сам є ф-цією від х, тобто розглянемо складну ф-цію y=f[φ(х)]. Якщо ф-ції y=f(u) та u=φ(х) диференційовані ф-ції відносно своїх аргументів, тоді похідна складної ф-ції: у'=f '(u)u'.У цьому випадку диференціал ф-ції:dy=f ‘[φ(x)]dx=f ’(u)u’dx=f'(u)du, враховуючи що u'dx = du, то dy=f ‘(u)du або df(u)=dy=f ‘(x)dx. Остання рівність означає, що формула диференціалу не змінюється, якщо замість функції від неза- лежної змінної х розглядати функцію від залежної змінної u. Ця властивість отримала назву інваріантності (тобто незмін­ності форми (формули) диференціалу).

97.Застосування диференціалу до наближених обчисле- нь. З наведених вище формул витікає, що ∆y=dy+α(∆х)∆х, тобто приріст ф-ції ∆у відрізняється від її диференціалу dy на нескінченно малу величину більш високого порядку, ніж dy≈f '(x)∆x. Тому при достатньо малих значеннях ∆y≈dy або f(x +∆х) - f(x)≈ f'(x)∆x.Чим менше значення ∆х, тим точніше формула. Формула використовується для наближених обчислень: f(x +∆х)≈ f(x) + f ’(x)∆x.

98. Теорема Ферма та Роля. Теорема Ферма: Якщо ди- ференційована на проміжку X функція y=f(x) досягає най- більшого або найменшого значення у внутрішній точці x_о цього проміжку, то похідна функції у цій точці дорівнює 0,тобто f ‘=(x₀).Теорема Роля: Нехай функція y=f(x) задо- вольняє наступним умовам:1)неперервна на відрізку [а;Ь]; 2)диференційована на інтервалі (а, Ь);3)на кінцях відрізку приймає рівні значення, тобто f(а)=f(Ь).Тоді в се- редині відрізку існує по меншій мірі одна така точка ξ є (а,Ь), в якій похідна функції дорівнює 0: f '(ξ) = 0. 5. Теорема Лагранжа та її висновки. Терема Лагранжа: Нехай ф-ція у= f(x) задовольняє наступним умовам: 1)неперервна на відрізку [а; Ь]; 2)диференційована на інтервалі (а: Ь).Тоді в середині відрізка існує, по крайній мірі, одна така точка ξ Є(а;Ь),в якій похідна дорівнює час- тці від ділення приросту функції на приріст аргументу на цьому відрізку, тобто

(b)-f(a)

f ‘(ξ)=----------- або

b-a

f(b)-f(a)=f ‘(ξ)(b-a).Наслідок: Якщо похідна ф-ції f(x) дорів- нює нулю, на деякому проміжку X, то функція постійна на цьому проміжку.

100.Пра-ло Лопіталя для розкриття невизначенос тей

Теорема: Границя відношення двох нескінченно-малих або нескінченно-великих функцій дорівнює границі відношення їх похідних (кінцеві або нескінченні), якщо остання існує у, певному розумінні. Тобто, якщо є невизначеність виду

(0/ 0) або (∞/∞) ,то limf(x)/g(x)=limf ‘(x)/g ‘(x).

x→x₀ x→x₀

Зауваження: Якщо границя відношення похідних є невизначеність типу (0/0) або (∞/∞), тоді можна знов використати правило Лопіталя, тобто перейти до границі відношення других похідних і т. д. Зауваження: Використан- ня правила Лопіталя до розкриття невизначеностей вигляду 0;∞ або ∞;∞ можливе лише після перетворення їх до вигля- ду (0/0) або (∞/∞).