2. Дифференциальные уравнения лини с распределенными параметрами

Рассмотрим двухпроводную однородную линию, физические параметры которой рав­номерно распределены по ее длине:

― активное сопротивление пары проводов на единицу длины [Ом/м], определяется по известной формуле , зависит от материала про­вода (γ ) и от ее температуры ;

― индуктивность пары проводов на единицу длины линии [Гн/м], оп­ре­деляется как отношение потокосцеплепия к току ( ), является ото­бра­жением магнитного поля ли­нии в ее схеме замещения, зависит от магнитных характеристик среды (μ) и геометрических размеров линии;

― активная проводимость между проводами на единицу длины линии [См/м], яв­ляется следствием несовершенства изоляции между проводами, зави­сит от электрических па­раметров среды (γ) и геометрических размеров линии;

― емкость между проводами на единицу длины линии [Ф/м], опреде­ля­ется как от­ношение заряда к напряжению( ), является отображением электрического поля линии в ее схеме замещения, зависит от электрических ха­рактеристик среды () и геометрических размеров линии.

Удельные параметры линии зависят от физических парамет­ров самих проводов и окружающий их среды, поэтому они получили название физических или первич­ных.

Разделим всю линию на элементарные участки длиной dх и рассмотрим один из таких участков, находящийся на расстоянии х от начала линии. Схема замещения участка будет иметь вид рис.154.Здесь u и i ― напряжение и ток в на­чале рассматриваемого участка. В конце участка напряжение и ток получают приращения: и .

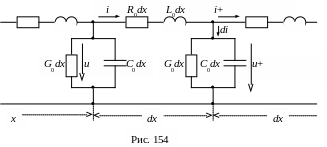
Функции напряжения и тока ( u, i ) зависят от двух параметров t и x, они изменяются в пространстве и во времени, поэтому дифференциальные уравне­ния для схемы замещения следует составлять в частных производных.

Уравнение по 2-му закону Кирхгофа для контура:

.

После упрощения получим:

(1).

По закону Ома и 1-му закону Кирхгофа:

В приведенном выражении пренебрегаем слагаемыми второго порядка малости, со­держащими .

По 1-му закону Кирхгофа для узла:

После упрощения получим:

 (2).

Уравнения (1) и (2) являются основными дифференциальными уравне­ниями двухпро­водной линии с распределенными параметрами, которые исполь­зуются для расчета как переходного, так и установившегося режима линии.

3. Решение уравнений линии с распределенными параметрами в устано­вившемся сину­соидальном режиме

Пусть напряжение и ток в линии с распределенными параметрами изме­няются по синусоидальному закону:

,

.

Заменим в дифференциальных уравнениях линии синусоидальные функ­ции и и их производные и соответствующими комплексными изображениями , , , :

(1)

(2)

В уравнениях (1) и (2) приняты обозначения:  ком­плекс­ное сопро­тивление линии на единицу длины [Ом /м],  комплексная проводимость линии на единицу длины [См /м].

Дифференцируем уравнение (2) по переменной х и делаем в него подста­новку из (1):

или

(3)

Решаем дифференциальное уравнение 2-го порядка (3) классическим ме­тодом. Характеристическое уравнение и его корни: от­куда   , + + .

Решение для искомой функции в общем виде:

,

где  безразмерная ком­плексная вели­чина, названная коэффициентом (постоянной) распространения,  комплексные постоянные интегрирования, которые определяются через граничные условия, т. е. через зна­чения искомых функций U(x), I(x) в за­данной точке линии, например в ее начале (х=0) или в ее конце (x=l).

Из уравнения (1) находим:

где 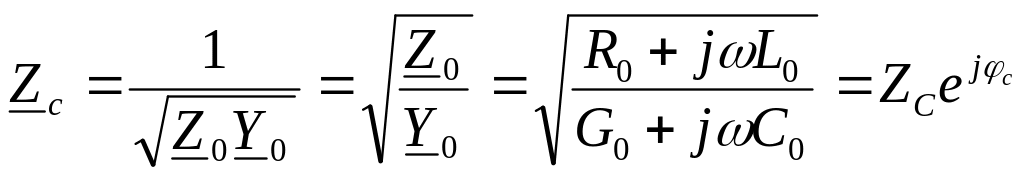― волновое или характери­стическое сопро­тивление линии.

Таким образом, решения для искомых функций U(x) и I(x) имеют вид:

, (4)

. (5)

Волновое сопротивление и постоянная распространения получили название вторичных параметров линии.

Выразим постоянные интегрирования и через граничные условия начала линии. При х = 0 , , подставим эти значения в уравне­ния (4) и (5):

Совместное решение этих уравнений позволяет определить постоянные интегрирова­ния: , .

Подставим полученные значения постоянных интегрирования в решения для искомых функций (4) и (5):

Полученные уравнения используются при расчетах цепей с распределен­ными пара­метрами в установившемся синусоидальном режиме.

Если принять х = l ,то получим значения параметров режима в конце ли­нии:

Выразим постоянные интегрирования через граничные условия конца ли­нии. Для этой цели в полученных ранее решениях (4) и (5) заменим переменные х на ly из условия x = ly, где l ― длина всей линии, а y ― расстояние от конца линии до рассматриваемой точки:

,

.

Здесь есть некоторые новые постоянные ин­тегри­рования.

При y = 0 , подставим эти значения в найден­ные урав­нения, получим:

Совместное решение этих уравнений позволяет определить постоянные интегриро­вания:

,

Подставляем значение постоянных в решение для искомых функций:

,

.

Полученные уравнения используются при расчете цепей с распределен­ными пара­метрами в установившемся синусоидальном режиме.

Если принять y = l , то получим значение параметров режима в начале ли­нии: