Граничные условия Кирхгофа

Устранив интегрирование по поверхности S₂, можно выразить возмущение в точке x_i через возмущение и его производную по нормали, взятые на бесконечной плоскости S₁, расположенной непосредственно за экраном:

(6.32)

Экран непрозрачен везде, кроме открытого отверстия, которое мы обозначим W. Кирхгоф принял следующие предположения.

1. На отверстии W распределение поля U и его производная имеют точно такие же значения, какие они имели бы в отсутствие экрана.

2. На той части поверхности S₁, которая лежит в области геометрической тени экрана, распределение поля и его производная тождественно равны нулю.

Эти граничные условия Кирхгофа лежат в основе скалярной теории дифракции. Первое условие позволяет определить возмущение, падающее на отверстие, пренебрегая наличием экрана, а второе дает возможность пренебречь интегрированием по всей поверхности, за исключением самого отверстия.

Формула дифракции Френеля — Кирхгофа

С учетом условий Кирхгофа выражение (6.30) запишем в виде

(6.33)

Обычно полагают, что расстояние r_i от отверстия до точки наблюдения во много раз больше длины волны. При этом выражение (6.27) можно преобразовать к следующему виду:

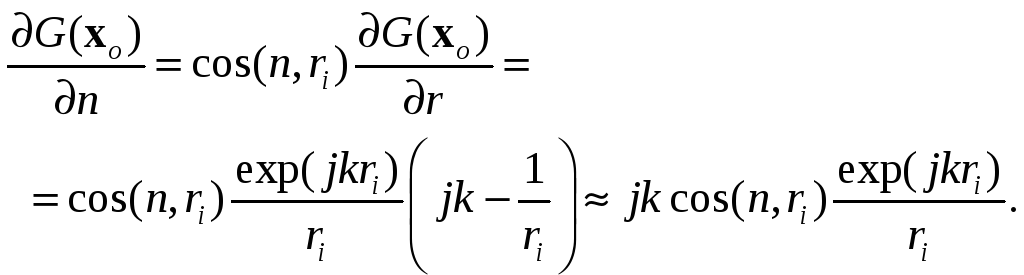_(6.34)

Подставляя приближенное выражение (6.34) и выражение (6.26) для G в (6.30), находим, что

(6.35)

Предположим, что на отверстие падает сферическая волна

(6.36)

исходящая из одиночного источника в точке x_s, расположенного на расстоянии r_s от x_o (см. рис. 6.8, а). Если расстояние r_s во много раз больше длины волны, то (6.35) сразу можно упростить:

(6.37)

Этот результат, справедливый для случая, когда отверстие освещается одиночным точечным источником, известен как формула дифракции Френеля — Кирхгофа.

Рассмотрим одну полезную интерпретацию формулы (6.37). Перепишем ее следующим образом:

(6.38)

(6.39)

Исходя из выражения (6.39), можем считать, что поле в точке x_i создается бесконечным множеством вторичных точечных источников, расположенных в пределах самого отверстия. Амплитуда вторичного источника, расположенного в точке x_o, пропорциональна амплитуде волны, исходящей из точки x_s.

Однако, во-первых, амплитуда вторичного источника отличается от амплитуды падающей волнымножителем ^–1, т. е. амплитуда колебания вторичного источника обратно пропорциональна длине волны. Во-вторых, эта амплитуда уменьшается за счет коэффициента наклона , который никогда не превышает единицы и всегда положителен. В результате каждому вторичному источнику соответствует анизотропная «картина направленности». В-третьих, фаза излучения вторичного источника в точке U(x_o) отличается от фазы падающей волны на 90°, что следует из наличия в выражении (6.39) множителя 1/j.

Эти любопытные свойства вторичных источников были, по существу, предсказаны Френелем. Математический вывод Кирхгофа показал, что эти свойства объясняются волновой природой света, при этом были уточнены некоторые интуитивные предположения Френеля.

Формула дифракции Рэлея — Зоммерфельда

Отметим, что приведенные выше краевые значения Кирхгофа математически противоречивы. Из теории потенциала известно, что если на некотором участке замкнутой поверхности функция и ее производные по нормали равны нулю, то они должны быть равны нулю и на всей замкнутой поверхности, которой является поверхность S. В этом случае выражение (6.39) вступает в противоречие с реальной физической ситуацией.

Для того чтобы выйти из этого положения, Зоммерфельд предложил в формуле (6.33) так изменить функцию Грина G, чтобы эта функция обращалась в нуль на всей поверхности W, но вывод приведенного выше выражения все же оставался справедливым.

Для этого новая функция Грина G_ должна подчиняться следующим условиям:

1) удовлетворять волновому уравнению;

2) быть равной нулю на поверхности W;

3) совпадать с функцией G при r_i = 0, т. е. в точке x_i.

В этом случае отпадает необходимость наложения граничных условий одновременно на U и , тем самым устраняются противоречия теории Кирхгофа. Введение этой вспомогательной функции ничего не меняет по существу, но облегчает математическое решение. При выполнении названных условий в выражении (6.33) устраняется математическое противоречие, а само оно значительно упрощается, так из него исключается первый член подынтегрального выражения.

Согласно Зоммерфельду, предположим, что функция G_ создается не только точечным источником, помещенным в точку x_i, но и вторым точечным источником в точке

Точка представляет собой зеркальное изображение точки x_i и лежит по другую сторону экрана (см. риc. 6.8, в). Пусть оба источника имеют одинаковую длину волны, а излучения этих источников сдвинуты по фазе на 180°. Функция Грина в этом случае имеет вид

(6.40)

где — расстояние между точками и x_o.

Функция (6.40) удовлетворяет всем условиям функции Грина. Она обращается в нуль на поверхности плоского экрана и переходит в функцию G в точке x_i. В этой точке функция так же как и функция G. Соответствующая производная от функции G_

Для точки x_o на поверхности S₁ имеем r_i = ; cos(n, r_i) = = Следовательно, на поверхности S₁ функция G_( x_o) = = 0, тогда

(6.41)

Таким образом, на всей поверхности S₁ функция Грина G_ в виде выражения (6.40) обращается в нуль, что устраняет противоречия теории Кирхгофа. Подставив функцию (6.41) в (6.33), получим

(6.42)

Выражение (6.42) — это дифракционное уравнение Рэлея — Зоммерфельда. Для упрощения расчетов обычно вводят некоторые ограничения на соотношения входящих в уравнение (6.42) параметров.