Фурье-преобразование

Формулы (7.27) и (7.28) выражают так называемое фурье-преобразование функции f(x). Отметим, что комплексная экспонента в формулах имеет разные знаки.

Для одномерного объекта с распределением интенсивности f(x) прямое фурье-преобразование позволяет найти частотную или спектральную характеристику. Это значит, что интенсивность объекта представляется в виде бесконечно большого набора гармонических составляющих всех пространственных частот , а модуль выражает ту долю, которая приходится на каждое выбранное значение частоты, т. е. выражает спектральную плотность.

Обратное фурье-преобразование позволяет восстановить распределение интенсивности по спектральной характеристике объекта.

Фурье-преобразования позволяют упростить расчеты распределения интенсивности в изображении, если известны распределение интенсивности в объекте и функция рассеяния системы.

Воспользуемся известной теоремой, которая формулируется так: фурье-преобразование некоторой функции, являющейся сверткой других функций, равно произведению фурье-преобра- зований функций, подвергаемых свертке.

Докажем эту теорему применительно к рассмотренному ранее примеру свертки, а именно к выражению интенсивности I_i(x) в точке изображения. Для формулы (7.11) напишем фурье-преобразование обеих частей равенства:

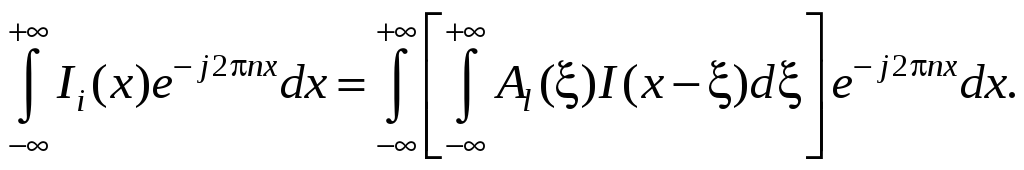(7.29)

Обозначим I_i() фурье-преобразование фунукции I_i(x), а в правой части равенства (7.29) выберем следующий порядок интегрирования:

(7.30)

Во внутреннем интеграле правой части (7.30) введем новую переменную x = x – . Тогда

и равенство (7.30) приобретет вид

(7.31)

т. е. действительно І_i() равно произведению фурье-преобра- зований функций, связанных операцией свертки (в данном случае функции распределения интенсивности в объекте и функции рассеяния).

Фурье-преобразование изображения

Результат, полученный выше, позволяет существенно упростить нашу основную задачу — вычисление интенсивности I_i(x) в плоскости изображения проекционной системы.

Действительно, теперь для решения этой задачи нет необходимости вычислять свертку распределения интенсивности в объекте I_o(x) с функцией рассеяния линии A_l(x). Значительно проще сделать это через фурье-преобразование, так как фурье-преобразование изображения равно произведению фурье-преобразований объекта I_o(x) и изображения изолированной линии A_l(x). Таким образом, если от распределения интенсивности в объекте I_o(x) перейти к фурье-преобразованию, т. е. к спектру пространственных частот объекта,

(7.32)

а от функции рассеяния линии A_l() — к фурье-преобразованию

(7.33)

то спектр пространственных частот изображения I_i(), т. е. фурье-преобразование от распределения интенсивности в изображении I_i(x), будет иметь вид

(7.34)

7.6. Оптическая передаточная функция

Из предыдущего параграфа следует очень важный вывод.

Если представить объект в виде суммы гармоник различных пространственных частот, можно оценить, какими они станут после прохождения оптической системы, т. е. в изображении. Для этого входные параметры каждой гармоники следует преобразовать с помощью соответствующего коэффициента A(). Просуммировав преобразованные гармоники, получим представление объекта после прохождения оптической системы, т. е. изображение.

Функция A(), определяющая, каким образом каждая частотная составляющая передается оптической системой с учетом дифракции, аберраций, ошибок изготовления оптической системы, называется оптической передаточной функцией (ОПФ) системы.

ОПФ, являющаяся, согласно выражению (7.33), преобразованием Фурье от функции рассеяния импульсной функции, представляет собой в общем случае комплексную функцию, которую можно записать в показательной форме через модуль комплексной функции T() и аргумент φ():

(7.35)

Естественно, ОПФ можно записать и в тригонометрической форме. Используя формулу Эйлера, имеем

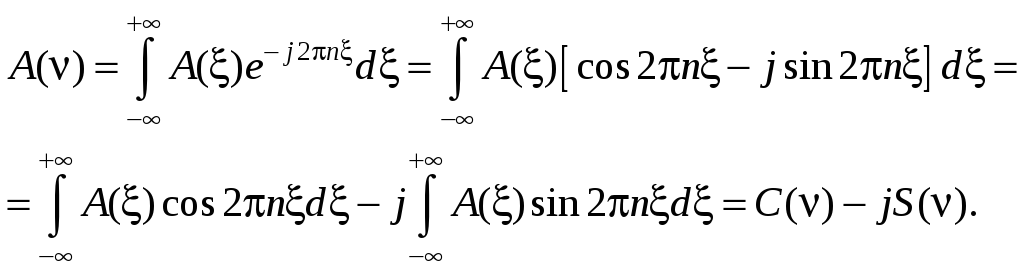_(7.36)

Интегралы, обозначенные через C и S, называются соответственно косинус-преобразованием и синус-преобразованием функции рассеяния и представляют собою действительную и мнимую части комплексной функции A(). Поэтому модуль комплексной функции

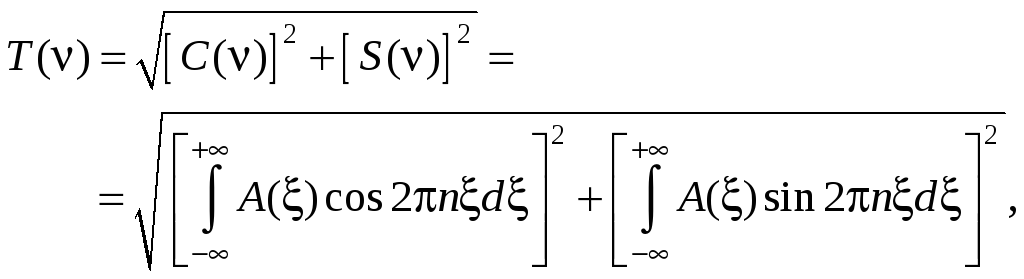_(7.37)

а аргумент может быть определен из соотношений

(7.38)

Для уяснения смысла модуля T() и аргумента () комплексной ОПФ рассмотрим более подробно, как изображается отдельная частотная составляющая объекта системой, имеющей известную функцию рассеяния.

Возьмем объект, имеющий косинусоидальное распределение интенсивности (рис. 7.6, а):

(7.39)

где I₀ — постоянная составляющая.

Если функцию рассеяния линии (при текущей переменной ξ) обозначить через A_l(), то интенсивность изображения можно записать в виде

(7.40)

Интеграл в первом слагаемом представляет собой нормированную функцию рассеяния линии и равен единице. В подынтегральном выражении второго слагаемого применим формулу косинуса разности двух углов:

(7.41)

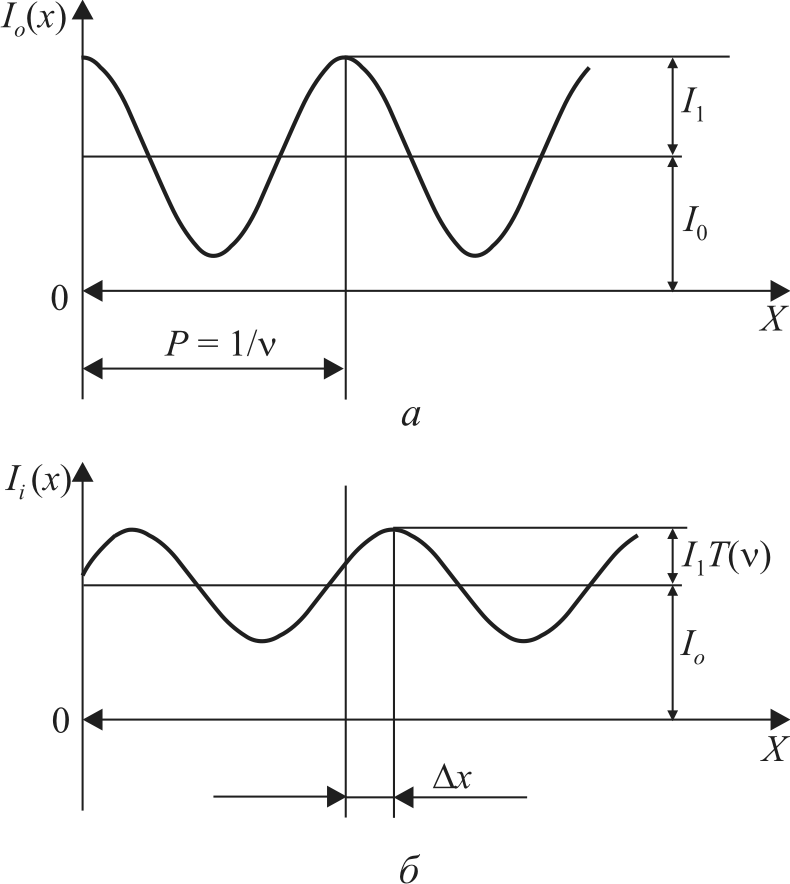
Рис. 7.6. Косинусоидальный объект (а) и его изображение (б)

Два интеграла в (7.41) — это знакомые нам по формуле (7.36) косинус-преобразование C и синус-преобразование S функции рассеяния. Следовательно, умножив и поделив на , получим

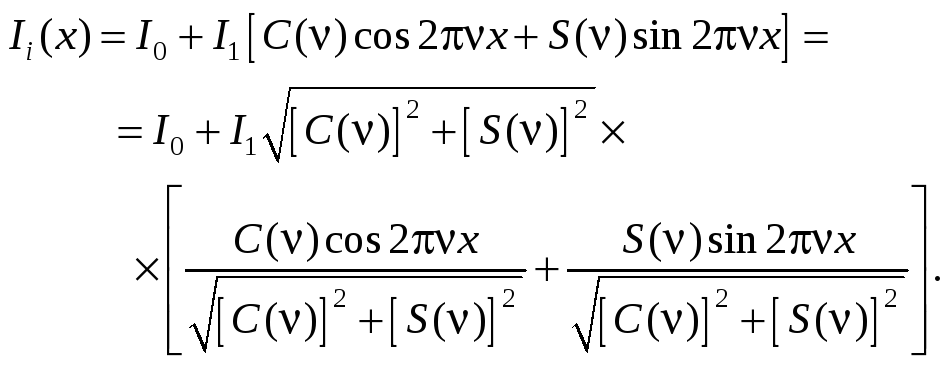_(7.42)

Дроби C() и S() согласно (7.38) равны

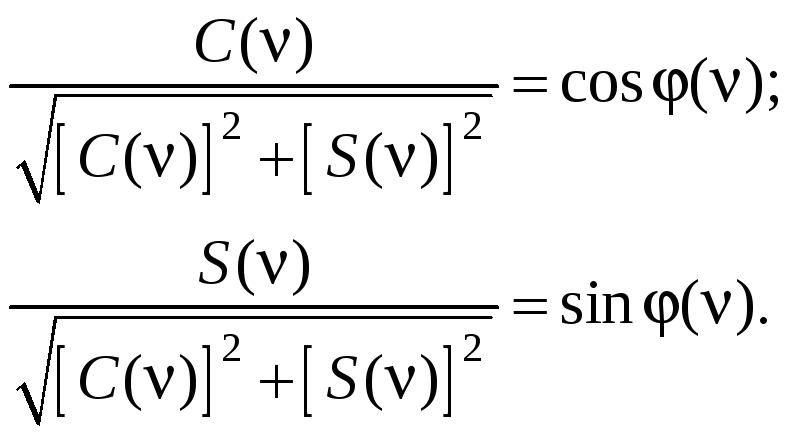(7.43)

Учитывая также выражение (7.37), получим

_(7.44)

Таким образом, изображение косинусоидального объекта (рис. 7.6, б) остается косинусоидальным и имеет такую же пространственную частоту, как объект. Тем не менее изображение (7.44) отличается от объекта (7.39) двумя особенностями.

Первая особенность состоит в том, что модуляция (отношение амплитуды переменной составляющей распределения к среднему значению — к постоянной составляющей) для изображения меньше, чем для объекта. В объекте m_o = I₁/I₀, а в изображении m_i = = I₁T()/I₀, т. е.

(7.45)

Таким образом, значение модуля T() оптической передаточной функции для каждой пространственной частоты равно отношению модуляции гармонической составляющей в изображении к модуляции этой составляющей в объекте и называется коэффициентом передачи модуляции (КПМ) системы.

Совокупность значений КПМ для различных пространственных частот составляет функцию передачи модуляции (ФПМ) системы.

Следует отметить, что для значения пространственной частоты  = 0 значение T() = 1, что легко проверить подстановкой  = 0 в выражение (7.37). Примерная форма ФПМ показана на рис. 7.7, а.

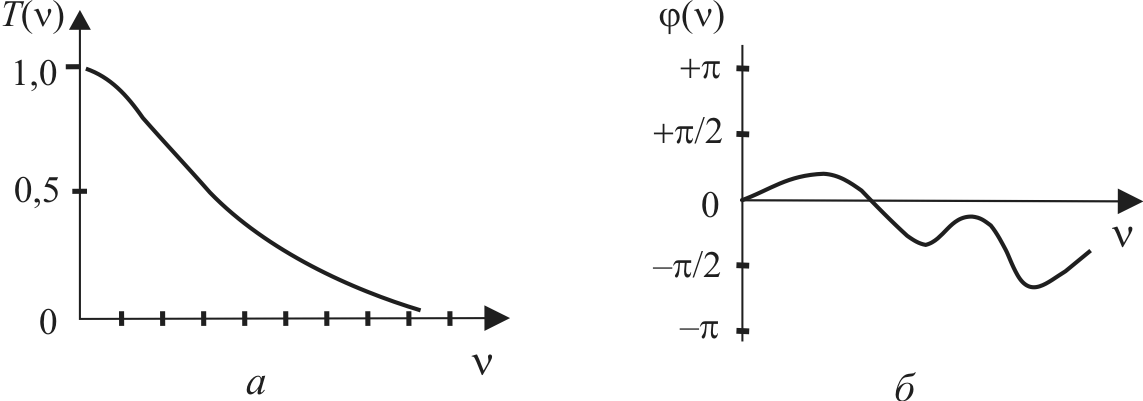
Рис. 7.7. Вид функции передачи модуляции (а) и фазы (б)

Вторая особенность заключается в том, что распределение интенсивности в изображении отличается от распределения в объекте еще и сдвигом косинусоиды на () (в угловой мере).

Совокупность значений сдвига (смещения) фазы () для различных пространственных частот составляет функцию передачи фазы (ФПФ) системы. Линейное смещение косинусоиды ∆x (рис. 7.7, б) должно составлять, очевидно, такую же часть от периода, т. е. от 1/, какую фазовый угол сдвига () составляет от 2π, т. е.

Для  = 0 угол () = 0, что легко проверить подстановкой  = = 0 в формулу (7.38).

Форма ФПФ существенно зависит от симметричности функции рассеяния A() относительно оси ординат.

В случае симметрии, т. е. если A() = A(–), функция рассеяния является четной. Тогда произведение — нечетная функция (ввиду нечетности синуса), а синус-преобразование S() в формуле (7.37) оказывается равным нулю для всех значений (как интеграл от нечетной функции в симметричных пределах), т. е. функция передачи фазы равна нулю или . Отметим, что при симметричной функции рассеяния A()

(7.46)

При асимметричной функции рассеяния (для оптических систем это может быть на краю поля зрения, при дефектах центрирования и др.) функция передачи фазы для может принимать значения между + и – (см. рис. 7.7, б).