7.4. Свертка

Простые по форме элементы объекта, такие, как точка или линия, изображаются проекционной оптической системой в виде функций рассеяния. Чтобы определить интенсивность I_i(x) в некоторой точке x изображения, нужно просуммировать ординаты функций рассеяния, полученные от точки объекта с той же координатой x и от соседних точек объекта, функции рассеяния которых вносят свой вклад в интенсивность в точке x.

Математическая операция, позволяющая провести такое построение, называется сверткой. Для пояснения смысла операции свертки воспользуемся свойствами прямоугольной (единичной импульсной) функции.

Рассмотрим последовательность прямоугольных импульсов f(x) (рис. 7.3, а), у которых с ростом номера уменьшается ширина, но увеличивается высота, в связи с чем площадь импульса остается постоянной и равной единице.

Рис. 7.3. Прямоугольные функции:

а — последовательность прямоугольных импульсов; б — единичный импульс; в — сдвиг и масштабирование единичного импульса

Выберем узкую длинную прямоугольную функцию x, определенную в интервале от до и имеющую высоту 1/ (рис. 7.3, б). При умножении функции x на постоянную (например, a) площадь под графиком функции также увеличится в a раз. Смещение графика этой функции вдоль оси X на расстояние b приведет к вычитанию b из переменной x: (x – b) (рис. 7.3, в).

Суммируя импульсные функции, масштабированные различными постоянными и смещенные на разные расстояния вдоль оси X, можно получить такие совокупности импульсов, которые будут описывать любые произвольные функции.

Рассмотрим последнее утверждение более подробно.

Согласно определению отклик пространственно инвариантной системы на сумму импульсов будет равен сумме откликов системы на каждый отдельный импульс. По известному отклику системы на единичный импульс можно найти отклик системы на единичный импульс, увеличенный в a раз и смещенный на расстояние b. Другими словами, мы можем найти отклик на каждый импульс из совокупности, составляющей I(x), т. е. отклик всей функции I(x).

Математически приведенное выше положение сформулируем следующим образом.

Во-первых, представим I(x) в виде суммы импульсных функций x (рис. 7.4, а) шириной  и высотой 1/. Для каждого конкретного значения x, например x =  (рис. 7.4, б), высота единичной функции равна I(x) и эта функция сдвинута на  от центра.

Соотнесем между собой значения функции I(x) и прямоугольной функции x. При x =  высота в раз больше высоты функции x, так как . Следовательно, прямоугольную функцию при x =  можно представить в виде

(7.6)

Обратим внимание на то, что — это сдвинутая прямоугольная функция, а I(x) — это, по существу, масштабный коэффициент — аналог a (см. рис. 7.3, в).

Изменяя значения , получаем набор прямоугольных функций, сумма которых описывает входную функцию, т. е. распределение интенсивности на объекте I_o(x):

(7.7)

Во-вторых, найдем отклик системы на отдельный импульс. Пусть прямоугольной функции x на входе оптической системы соответствует функция A_l(x) на выходе (рис. 7.4, в).

Из пространственной инвариантности системы следует, что смещение входной функции на  вызывает такое же смещение выходной функции A_l(x), не изменяя ее вида. Таким образом, входная прямоугольная функция (7.6) размывается оптической системой (рис. 7.4, г) и на выходе описывается выражением

(7.8)

В-третьих, объединим отклики на входные импульсы (см. рис. 7.4, г). Совокупности импульсных функций, описывающих распределение интенсивности на объекте I_o(x), соответствует сумма выходных функций, описывающих распределения интенсивности в изображении I_i(x):

(7.9)

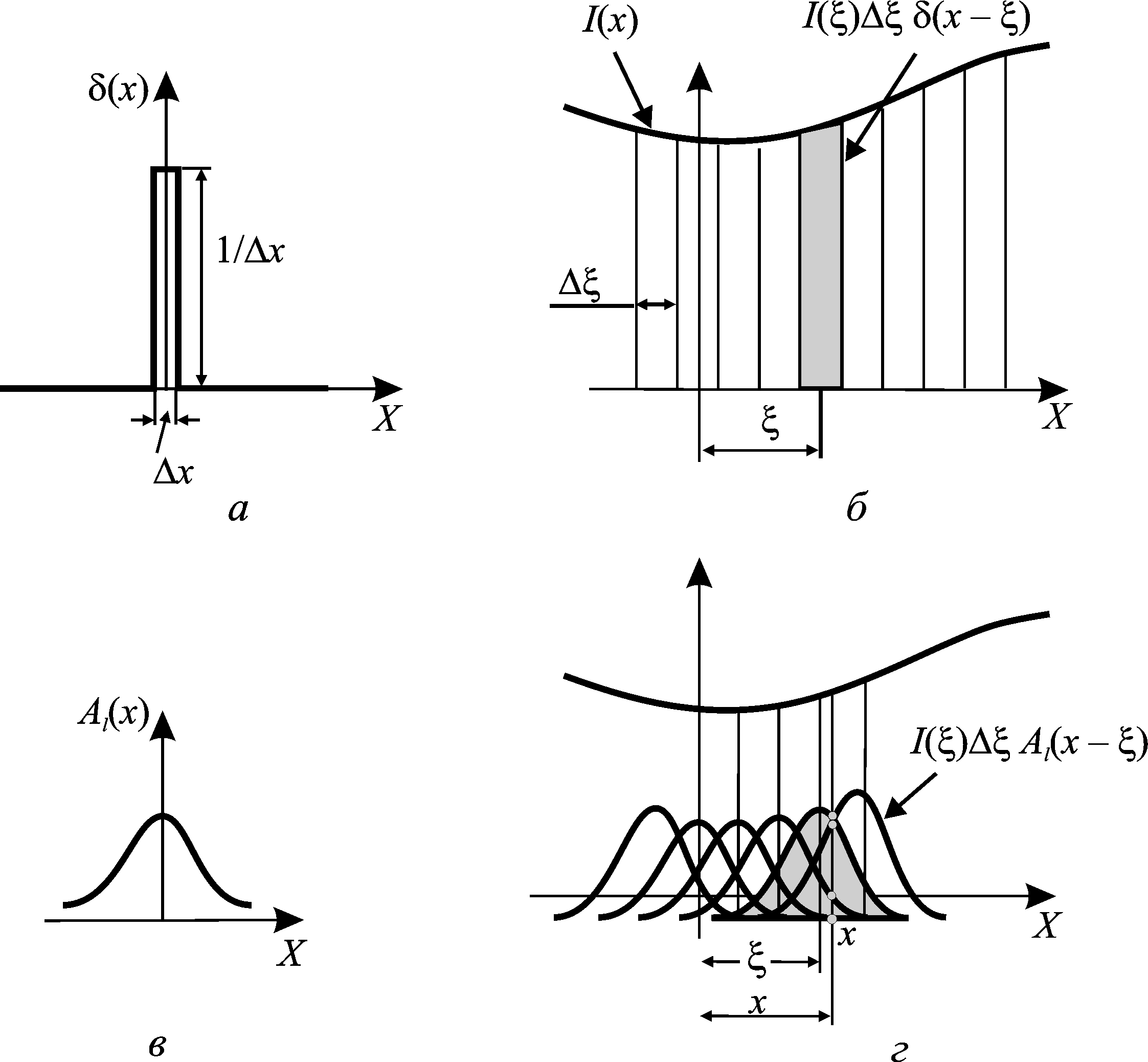
Рис. 7.4. Свертка функции с откликом системы:

а — прямоугольная функция; б — входная функция в виде совокупности прямоугольных функций; в — отклик системы (функция рассеяния); г — формирование свертки в точке с координатой x

Заменим теперь конечное приращение  бесконечно малым d. При этом сумма переходит в интеграл:

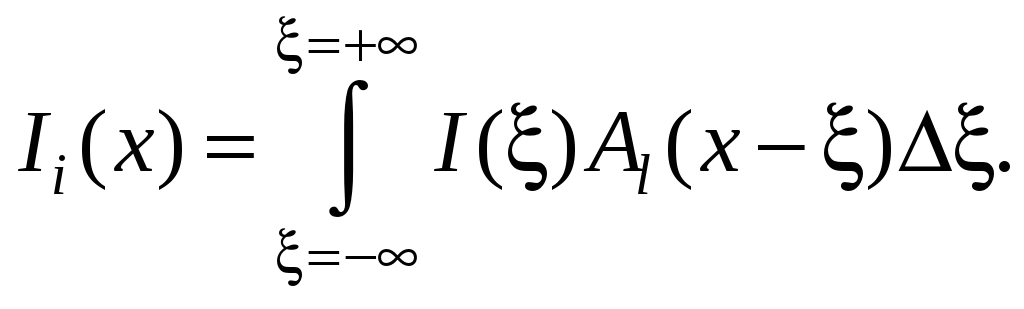(7.10)

Выражение (7.10) представляет собой интеграл свертки входной функции и отклика на узкую импульсную функцию.

Важным свойством интеграла свертки является коммутативность, которая в исследуемом случае проявляется следующим образом. Отметим, что импульсная функция, отстоящая от точки x на величину , т. е. в точке (x – ), имеет ординату I(x – ). Очевидно, что соответствующая функция рассеяния этого импульса на расстоянии , т. е. в точке x, имеет ординату A_l(), умноженную на значение функции в точке (x – ): I(x – )A_l().

Объединив функции рассеяния (отклики на входные импульсные функции), получим

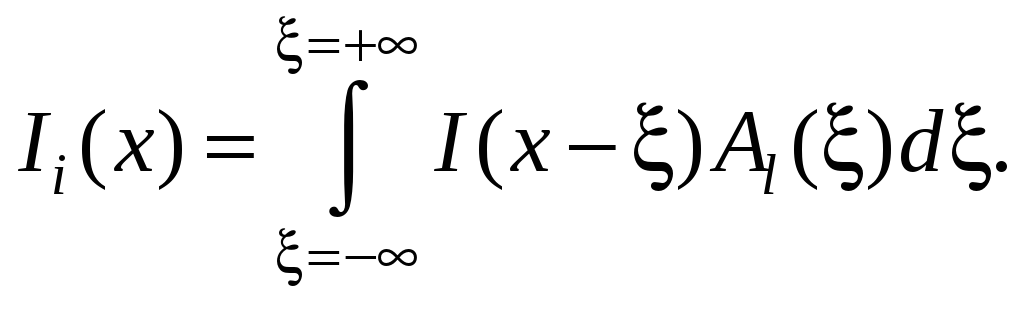(7.11)

Уравнение (7.11) эквивалентно уравнению (7.10), т.е. мы показали, что интеграл свертки действительно обладает свойством коммутативности.

Расчет распределения интенсивности в изображении может быть существенно упрощен при использовании преобразований Фурье.