7.5. Фурье-преобразования в оптике Понятие пространственной частоты

В параграфе 7.2 мы рассматривали объект как совокупность элементов простой формы: точек или линий. Но можно представить произвольный объект как совокупность элементарных пространственных составляющих (гармоник), интенсивность которых изменяется по синусоидальному или косинусоидальному закону и которые отличаются друг от друга по частоте, амплитуде и фазе.

Применительно к решетке пространственная частота в соответствии с формулой (7.1) равна количеству ее периодов, размещающихся на единице длины. Так, n-я пространственная гармоника периода P имеет период P/n, что соответствует пространственной частоте n/P, которая представляет собой число повторений на единице длины изображения.

Ряды Фурье

Периодическую функцию f(x) аргумента x, имеющую период P, т. е. пространственную частоту  = 1/P, можно представить в виде суммы синусоид или косинусоид, имеющих частоты , 2, 3, ... , n и периоды P , P/2, P/3, ..., P/n:

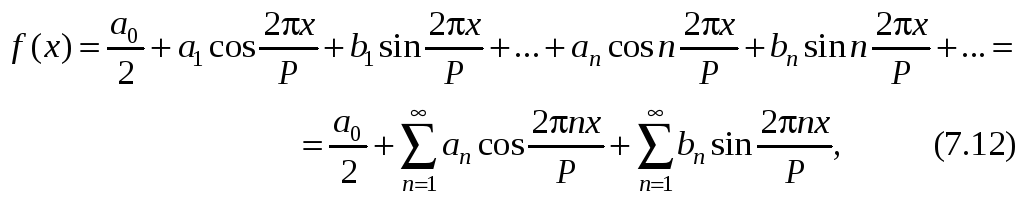
где P измеряется в миллиметрах, а  — в единицах на миллиметр.

Коэффициенты такого ряда определяются по формулам

(7.13)

Легко убедиться, что для четной функции все b_n = 0; для нечетной функции все a_n = 0.

Тестовые решетки с одинаковыми прозрачными и непрозрачными полосами (см. рис. 7.1, а), имеющие прямоугольное (П-образное) пропускание, могут быть описаны рядами Фурье:

(7.14)

(7.15)

Уравнение (7.14) соответствует расположению начала координат в центре окна (рис. 7.5, а), а уравнение (7.15) — случаю, когда начало координат совпадает с границей окна (рис. 7.5, б).

На рис. 7.5, в в пределах одного периода показаны частные суммы двух и трех членов ряда Фурье. Увеличение числа членов ряда Фурье делает суммарную функцию все более похожей на исходное прямоугольное распределение.

Ряд Фурье в комплексной форме

Разложение Фурье может быть записано в более простой форме с помощью комплексных экспоненциальных функций. Используем для этого экспоненциальные выражения для косинуса и синуса, являющиеся следствием формулы Эйлера:

(7.16)

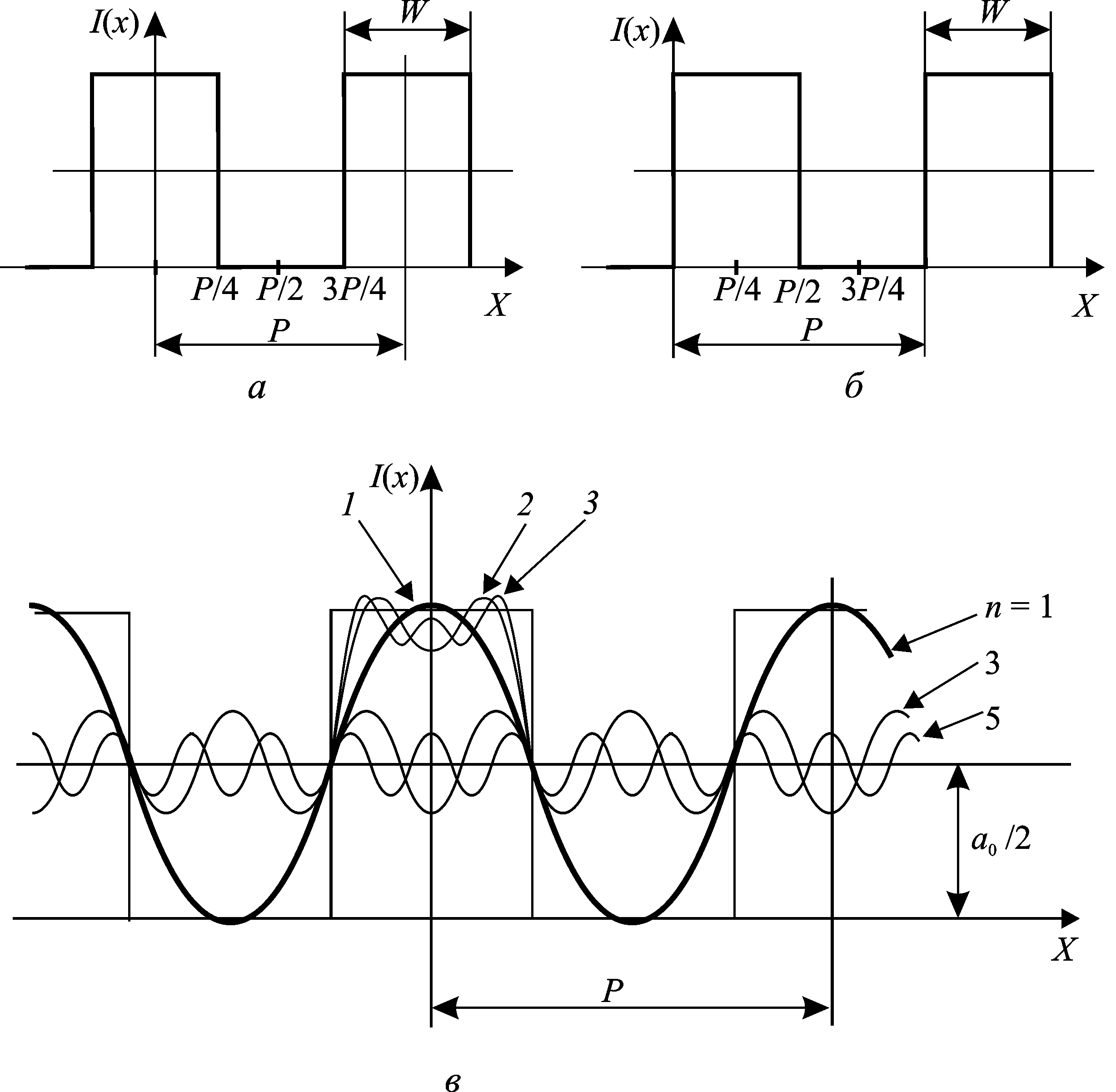
Рис. 7.5. Представление функции рядом Фурье:

1 — первый член ряда; 2 — сумма двух членов ряда Фурье; 3 — сумма трех членов ряда Фурье

Представим общий член выражения (7.13) в виде

(7.17)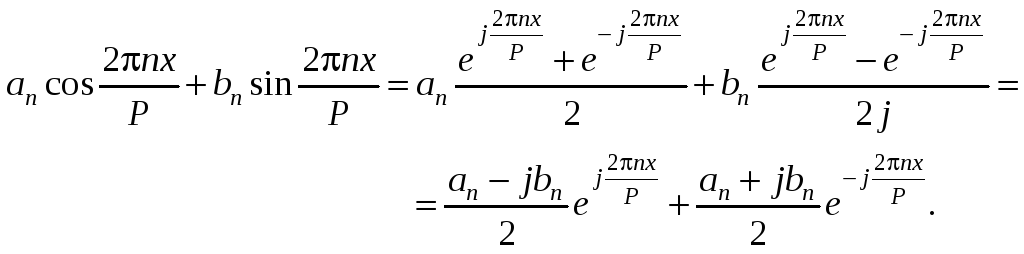

Если мы обозначим

(7.18)

то формула (7.13) примет вид

(7.19)

Отметим, что суммирование ведется по целым (как положительным, так и отрицательным) значениям n, включая также и нуль. При этом комплексные коэффициенты и поэтому , где звездочка означает комплексное сопряжение.

Формула (7.19) имеет очень простой вид. Покажем, что существует также очень простая формула для определения коэффициентов C по заданной функции f(x). Подставим для этого значения a₀, a_n, b_n из формул (7.14) в формулы (7.18) и получим:

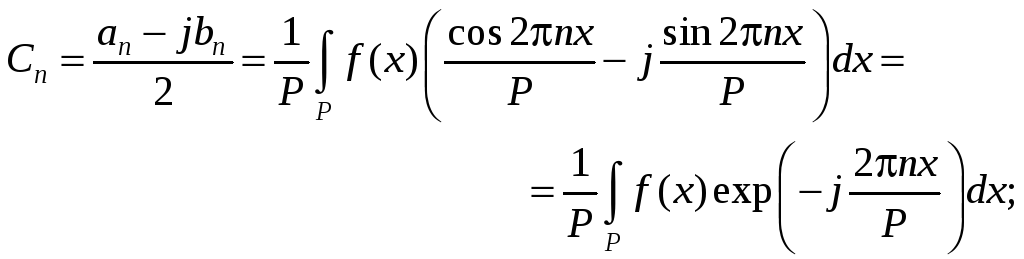_(7.20)

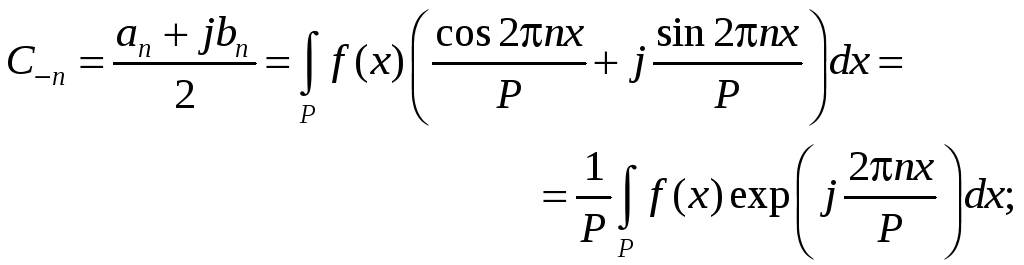_(7.21)

(7.22)

Формулы (7.20) – (7.22) можно объединить в одну формулу

(7.23)

где n принимает все положительные и отрицательные целые значения, включая нуль. Таким образом, в комплексной форме разложение Фурье имеет вид

(7.24)

(7.25)

Интеграл Фурье

При увеличении периода P пространственные частоты становятся ближе друг к другу. Это означает, что в предельном случае непериодическая функция может содержать все частоты. Разложение таких функций осуществляется с помощью интеграла Фурье. Для разложения такой функции в выражение (7.19) подставим значение C_n из (7.23):

(7.26)

Непериодическую функцию можно рассматривать как предельный случай периодической функции при стремлении периода к бесконечности, т. е. когда . В рассматриваемой формуле множители n/P можно принять за дискретные значения

...;

переменной , непрерывно меняющейся от до .

Приращение переменной . При можно ввести замену . С учетом этой замены сумма (7.26) переходит в интеграл и мы получаем выражение интеграла Фурье в комплексной форме:

(7.27)

причем функция определяется через f(x) формулой

(7.28)