Интегральная теорема Гельмгольца — Кирхгофа

Рассмотрим прежде всего выбор функции Грина, сделанный Кирхгофом, и интегральную теорему, следующую из этого вывода.

По существу, нам необходимо выразить оптическое возмущение в точке x_i через значение этого возмущения на поверхности S (рис. 6.8, а). Следуя Кирхгофу, выберем в качестве функции Грина G(x) сферическую волну единичной амплитуды, распространяющуюся из точки x_i. Такая функция G (так называемая функция Грина свободного пространства) для произвольной точки x_o поверхности S имеет вид

(6.22)

где — длина вектора, направленного из точки x_i в точку x_o.

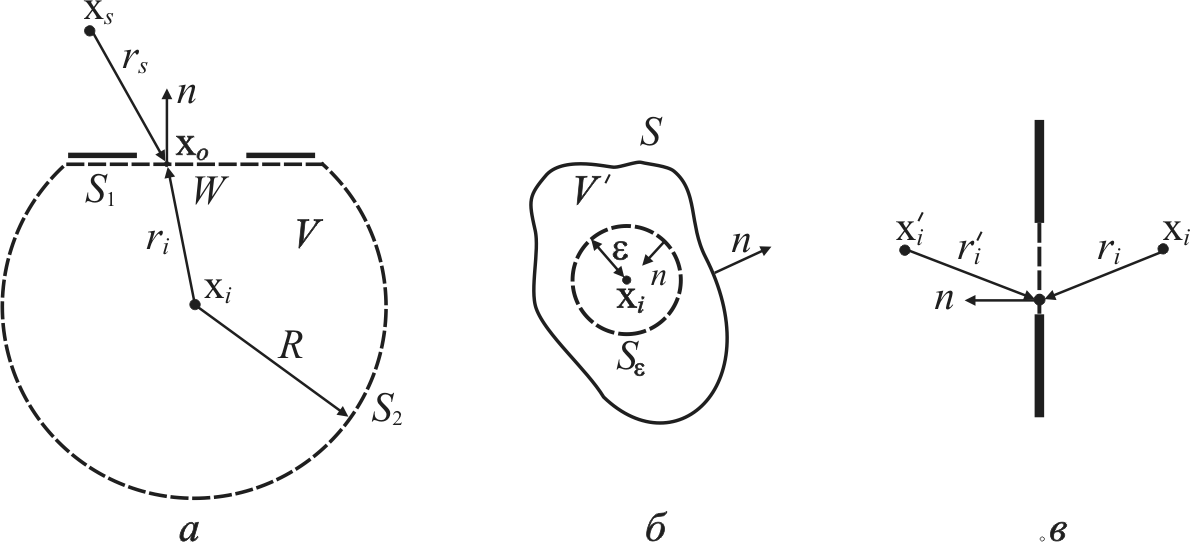
Рис. 6.8. Дифракция на плоском экране

а — трактовка Кирхгофа; б — поверхность интегрирования; в — трактовка Зоммерфельда

Для использования теоремы Грина необходимо, чтобы функция G(x), ее первая и вторая производные были непрерывными в объеме V, ограниченном поверхностью S. Поскольку точка x_i является точкой разрыва (при x_i функция G(x) имеет особенность), ее необходимо исключить из области интегрирования. Для этого окружим x_i небольшой сферической поверхностью S_ радиусом  (рис. 6.8, б). Затем применим теорему Грина, причем интегрирование будем вести по объему заключенному между поверхностями S и S_.

Поверхностью интегрирования будет в данном случае поверхность = S + S_. Внутри объема возмущение G(x), представляющее собой расходящуюся сферическую волну, удовлетворяет уравнению Гельмгольца

(6.23)

Используя оба уравнения Гельмгольца (6.20) и (6.23) для преобразования левой части формулы Грина, получаем

(6.24)

Тогда теорема (6.21) преобразуется к виду

или

(6.25)

В формуле (6.25) функция U(x) характеризует возмущение поля на поверхности в некоторой точке x_o, а функция G(x) —воздействие на эту точку сферической волны единичной амплитуды, расходящейся из точки x_i, т. е. функции Грина. Поэтому для этой точки

(6.26)

Производная по нормали функции Грина приобретает вид

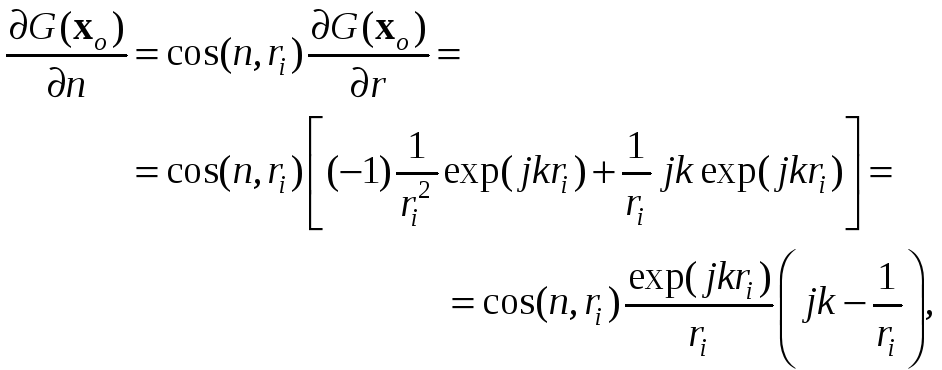_(6.27)

где cos(n, r_i) — косинус угла между направлением внешней нормали n и вектором r_i, соединяющим точки x_i и x_o.

Для частного случая, когда точка x_o лежит на поверхности S_, имеем cos(n, r_i) = –1 и выражения (6.26) и (6.27) принимают вид

(6.28)

Если , то в силу непрерывности функции U (и ее производных) в точке x_i можно записать

_(6.29)

При этом полагалось, что интеграл — это объем, опирающийся на площадь S_. При площадь значение а объем равен произведению значений площади основания и функции в точке x_i. Подстановка полученного результата в (6.25) дает

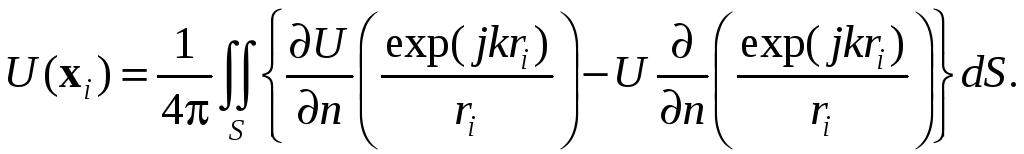(6.30)

Соотношение (6.30) представляет собой математическую запись интегральной теоремы Гельмгольца — Кирхгофа. Она позволяет выразить параметры поля в любой точке x_i через граничные параметры волны на любой замкнутой поверхности, окружающей эту точку.

Применение интегральной теоремы

Рассмотрим задачу о дифракции на отверстии в бесконечном непрозрачном экране. Предполагается, что возмущение от точечного источника с координатой x_s падает сверху на непрозрачный экран с отверстием, как показано на рис. 6.8, а. Необходимо рассчитать параметры поля в точке x_i за отверстием.

Воспользуемся интегральной теоремой Гельмгольца — Кирхгофа, выбрав соответствующим образом поверхность интегрирования. Следуя Кирхгофу, возьмем замкнутую поверхность S таким образом, чтобы она состояла из двух частей (см. рис. 6.8, а). Пусть плоская поверхность S₁, лежащая сразу за дифракционным экраном, замыкается большим сферическим колпаком S₂ радиусом R с центром в рассматриваемой точке x_i. Полная замкнутая поверхность S образована поверхностями S₁ и S₂, поэтому интеграл (6.21) имеет вид

(6.31)

где, как и прежде,

При увеличении R поверхность S₂ принимает форму полусферической оболочки. Можно показать, что интеграл по S₂ не будет давать вклада в общий интеграл.