6.5.1. Доверительные интервалы для оценки математического ожидания нормального распределения случайной величины

Доверительным называют интервал (^*–,^*+), который покрывает неизвестный параметр с заданной надёжностью, где,^*– статистическая характеристика, найденная по данным выборки, которая служит оценкой неизвестного параметра. Отклонение неизвестного параметраот его оценки^*задаётся величиной положительной>0,так как их разность задаётся по модулю |–^*| <. Чем меньше отклонение, тем точнее оценка. Рассмотрим нахождение доверительного интервала для математического ожидания нормально распределенной случайной величины. Из теории вероятностей интервальные вероятности для нормального распределения N(a,) определяются формулой (5.20):

P (|X– a| ≤ ) = 2Ф(/) = 2Ф(t),

(6.9)

где t = /.

Пусть случайая величина Х генеральной совокупности распределена нормально. Требуется оценить неизвестное математическое ожидание по выборочной средней. Выборочную среднюю можно рассматривать как случайую величину, которая изменяется от выборки к выборке.

Из теории вероятностей дискретной случайной величины известны положения для числовых характеристик среднего арифметического. В частности:

1. Дисперсия среднего арифметического n одинаково распределённых взаимно независимых случайных величин в n раз меньше дисперсии D каждой из величин:

.

2. Среднее квадратическое отклонение n одинаково распределённых взаимно независимых случайных величин соответственно равно:

.

Заменив в (6.9) случайую величину Х на выборочную среднююx,на

можно (6.9) переписать в виде:

,

(6.9а)

где:

.

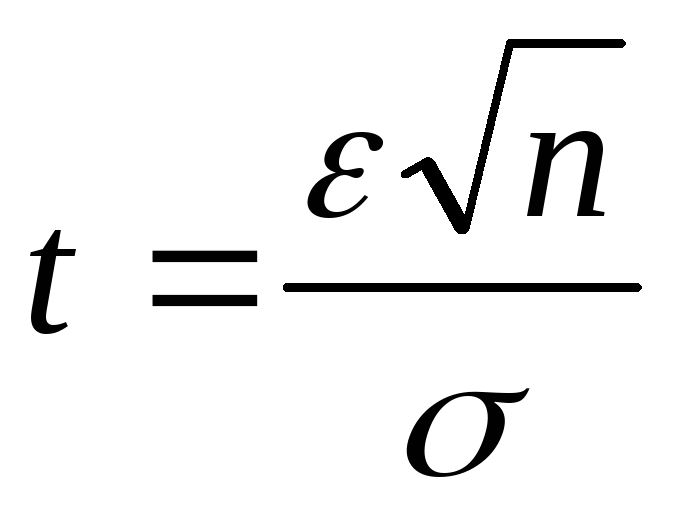Можно найти отклонение неизвестного параметра от его оценки:

.

(6.10)

Если в (6.9а) рассмотреть неравенство , то из него можно выразить неизвестное математическое ожидание а:

.

(6.11)

Если в (6.11) подставить вместо значение из (6.10), то получим доверительный интервал для математического ожидания нормально распределенной случайной величины.

.

(6.12)

Вероятность

определяется законом нормального распределения, если известна дисперсия D=².

Если дисперсия неизвестна, а лишь подсчитано ее несмещённое значение

,

то вероятность

определяется законом распределения Стьюдента со степенями свободы k = n–1. С увеличением степеней свободы k, то есть с увеличением объема выборки, распределение Стьюдента стремится к нормальному.

6.5.2. Доверительные интервалы для математического ожидания при известной дисперсии

Пусть случайая величина Х генеральной совокупности распределена нормально, учитывая, что дисперсия и среднее квадратическое отклонение этого распределения известны. Требуется оценить неизвестное математическое ожидание по выборочной средней. В данном случае задача сводится к нахождению доверительного интервала для математического ожидания с надёжностью. Если задаться значением доверительной вероятности (надёжности), то можно найти вероятность попадания в интервал для неизвестного математического ожидания, используя формулу (6.9а):

(6.13)

где – вероятность покрытия математического ожидания а доверительным интервалом.

Если приравнять правые части (6.9а) и (6.13), то получим:

 = 2Ф(t).

(6.14)

где Ф(t) – функция Лапласа (5.17а).

В результате можно сформулировать алгоритм отыскания границ доверительного интервала для математического ожидания, если известна дисперсия D = ²:

1. Задать значение надёжности – .

2. Из (6.14) выразить Ф(t) = 0,5. Выбрать значение t из таблицы для функции Лапласа по значению Ф(t) (см. Приложение 1).

3. Вычислить отклонение по формуле (6.10).

4. Записать доверительный интервал по формуле (6.12) такой, что с вероятностью выполняется неравенство:

.

(6.15)

Пример 5.

Случайная величина Х имеет нормальное распределение. Найти доверительные интервалы для оценки с надежностью = 0,96 неизвестного математического ожидания а, если даны:

1) генеральное среднее квадратическое отклонение = 5;

2) выборочная средняя ;

3) объём выборки n = 49.

Решение.

В формуле (6.15) интервальной оценки математического ожидания ас надёжностьювсе величины, кроме t, известны. Значение t можно найти, используя (6.14):= 2Ф(t) = 0,96. Ф(t) = 0,48.

По таблице Приложения 1 для функции Лапласа Ф(t) = 0,48 находят соответствующее значение t = 2,06. Следовательно, . Подставив в формулу (6.12) вычисленное значение, можно получить доверительный интервал: 30-1,47 < a < 30+1,47.

Искомый доверительный интервал для оценки с надёжностью = 0,96 неизвестного математического ожидания равен: 28,53 < a < 31,47.