Задачник по физике

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Коломенский институт филиал МГМУ

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

(12) Tmin = t =

L(υ1 +υ2cosα)

.pdf

Скачиваний:

Добавлен:

17.03.2016

Размер:

2.49 Mб

Скачать

☆

<<< < Предыдущая 1 2 34 / 224 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 > Следующая >>>

времени и приравниванию	ее к	нулю
(r&(t)= 0).		XOY
Прямоугольную систему	координат	XOY

выбираем неподвижной с началом в точке А, часы включаются в момент начала движения точек P1, P2 (см. рис.).

4*. Составим полную систему уравнений для написания функции r(t) в общем виде и вычисления искомой величины Tmin . Движение точки P1 на отрезке АВ описывается законом

равномерного движения вида:

x1(t) = x01 +υ0 x1t; x01 = 0; υ0 x1 =υ1;

y1(t) = 0,

и движение точки P2 на отрезке ВС – законом равномерного движения вида:

x2 (t) = x02 +υ0 x2t;	x02 = L;	υ0 x2 = −υ2 cosα;
y2 (t) = y02 +υ0 y2t;	y02 = 0;	υ0 y2 = −υ2 sinα.

Таким

образом,

имеем следующую

систему

для

представления искомой функции r(t) и величины Tmin :

(1)

(t) =υ

t ,

y1(t) = 0,

(2)

(3)

(t)

= L −υ

tcosα,

(4)

y2(t) =υ2tsinα,

r(t) =

(x2(t) − x1(t))2 + (y2(t) − y1(t))2 ,

(5)

r (t) = 0,

(6)

Tmin = корень(6).

(7)

Система семи уравнений (1) – (7)

является замкнутой, так

как содержит семь неизвестных величин:

x1,

x2 , y1,

y2 ,

r , и

Tmin .

5*. Исключим вначале

неизвестные величины

x2 ,

подставив (1) и (3) в (5) (получим систему пяти уравнений с пятью неизвестными), затем освободимся от неизвестных величин y1 и

- 31 -

y2 , подставив (2) и (4) в (5) (получим систему трех уравнений с тремя неизвестными):

(2)(4)

(8)

(6)(7)

(9)

(6)

(7)

y1(t) = 0,

y2(t) =υ2tsinα,

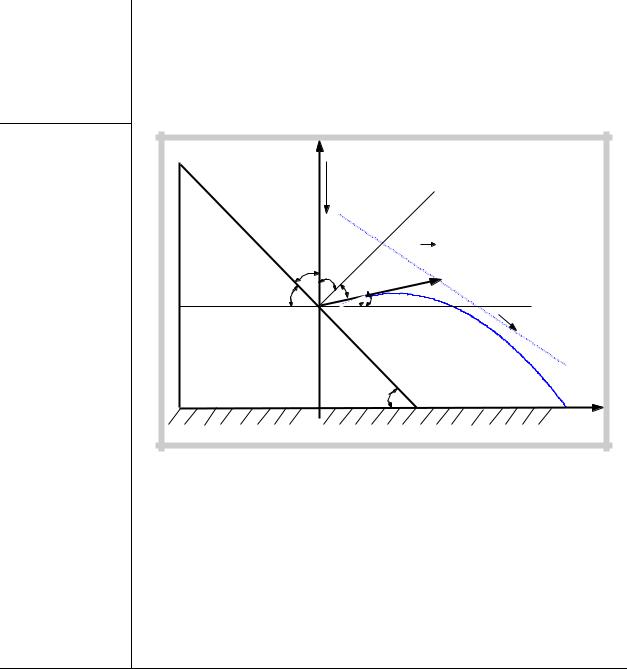
r(t) = (L −υ2tcosα −υ1 t)2 + (y2(t) − y1(t))2 ,

r (t) = 0,

Tmin = корень(6).

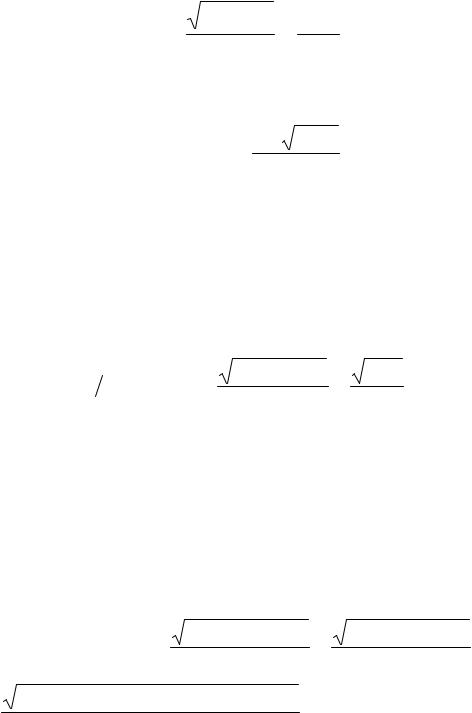
r(t) = 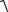(L −υ2tcosα −υ1 t)2 + (υ2tsinα)2 ,

r (t) = 0,

Tmin = корень(6).

Подставляя (9) в (6), имеем одно уравнение с одной неизвестной величиной (t = Tmin ):

(10)

dr(t)

2(− L + (υ1 +

υ2cosα)t)(υ1 +υ2cosα)+ 2υ22 sin2 α t

= 0 .

2 (L

−υ

2tcos

α −υ

+ υ

2t sin

1t)

(

)

Уравнению (10) эквивалентна следующая система:

α t = 0,

(11)

(− L + (υ1 +υ2cosα)t)(υ1 +υ2cosα)+υ2 sin

(L −υ2tcosα

≠ 0.

(12)

−υ1t) + (υ2t sin

α)

После выполнения несложных преобразований выражения (11) получаем величину t, которая и является искомой величиной

Tmin :

Заметим, что, подставляя (12) в (9), можно определить, чему равно расстояние в этот момент времени между точками P1 и P2 .

6*. Проверка размерности единицы измерения полученной

величины Tmin :

[Tmin ]= мм2 /мc/2с = c.

- 32 -

7*. Анализ задачи. Проанализируем формулу (8) для различных предельных случаев:

a)L=0, Tmin=0 – очевидно, верно;

b)α=0 (точки движутся вдоль одной прямой навстречу

друг другу),	Tmin =	L		– разумно, так как
		(υ1 +υ2 )

сумма скоростей в знаменателе представляет относительную скорость движения двух точек, то есть скорость их сближения;

c) равна нулю одна из скоростей, например, υ2 = 0,

, что вполне разумно,

так как встречи как

υ1

min

таковой не произойдет, а точка P1 достигнет границы

своего пути.

8*. Произведем расчет величины Tmin :

12(5 + 8 * 0,5)

= 108 ≈ 9,9 10−1 (c).

min

25 + 5 * 8 * 0,5 + 64

109

9*. Ответ:

Tmin =

L(υ1 +υ2cosα)

≈ 9,9 10

-1

υ2

+υ υ

cosα +υ2

***************

Задача 2

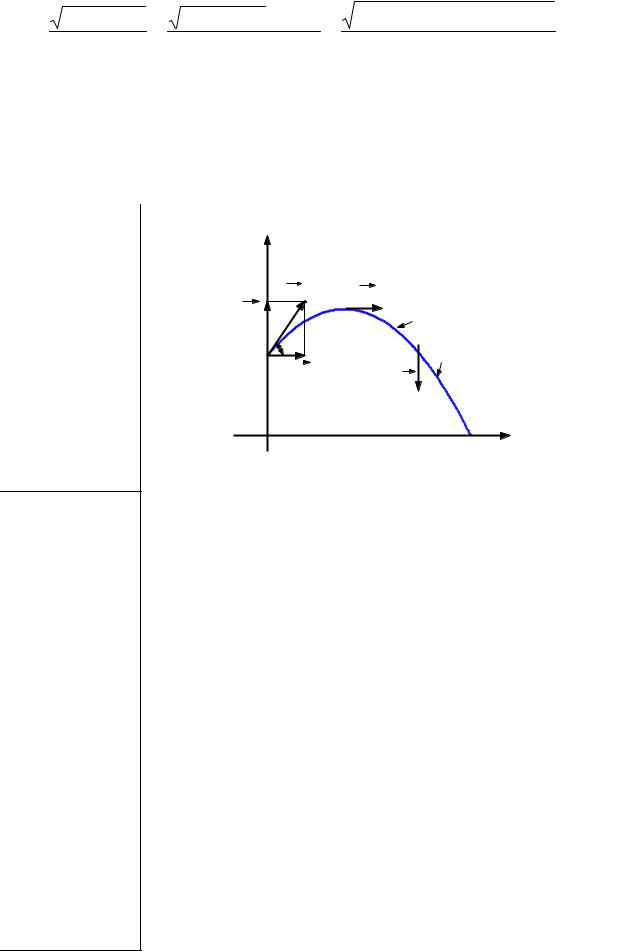
Мяч падает с высоты H = 10 м. На высоте h = 2 м от поверхности земли он абсолютно упруго ударяется о наклонную плоскость, расположенную под углом α = 30° к горизонту. Найти полное время T движения мяча.

1*.Дано:	Решение.
3*.	Анализ задачи. Выберем систему координат с

H = 10 м, началом отсчета в точке 0 (см. рис. ниже). Часы включаем в момент начала движения мяча с высоты h = 2 м, H. Очевидно, мяч можно считать материальной точкой. На участке АВ движение мяча является

α= 30°=π/6, прямолинейным и равноускоренным, на участке BD

–криволинейным и равнопеременным. Точка D, как

g=9,8 м/с2. явствует из соотношения высот (H>h), окажется на горизонтальном участке OD, то есть за пределами

- 33 -

наклонной плоскости. Поэтому рисунок охватывает
только один случай расположения точки D (случай
расположения точки D на наклонной плоскости не
рассматривается).			T найдем как сумму
Искомое	полное	время	T найдем как сумму
T −?	YH.A
	YH.A		2*.
	(π−α)		v B
	αh.α	β=α
	αh.α	γ=π\|2−2α
	B		.
	.		.
		α	D
	0		S	X
времен TB (движение мяча			на участке АВ) и	TD
(движение мяча на участке BD). Будем использовать
принцип	независимости движений по осям			OX
(равномерное и прямолинейное движение) и				OY
(равнопеременное и криволинейное движение).
Кроме того, в точке B будем использовать условие
абсолютно упругого удара, откуда, как следует из
геометрических построений рисунка, α=β и γ=π/2–
2α.

4*. Составим полную систему уравнений. Движение мяча описывается законом равноускоренного движения на участке AB, по оси ОY:

(t) = y

+υ

t +

= H ,

= 0,

a = −g,

+ at,

a = −g;

υy (t) =υ01

на участке BD – законом равномерного и прямолинейного движения по оси OX:

x(t) = x0 +υBx t,

x0 = 0, υBx =υB sin 2α

изаконом равнопеременного движения по оси OY:

-34 -

(t) = y

+υ

t + at

= h,

=υ

cos 2α,

a = −g,

(t) =υBy + at,

a = −g.

υy

Применяя записанные уравнения для точек B и D (см. рис. выше) получаем следующую систему уравнений:

(1)	h = H − gT 2		2 ,
		B
	−υB = −gTB ,
(2)	−υB = −gTB ,
	0 = h +υByTD − gTD2 2,
(3)	0 = h +υByTD − gTD2 2,
	υBy =υB cos 2α,
(4)	υBy =υB cos 2α,
(5)	T = T	+T .
	B	D

где S – дальность полета мяча по оси OX, а υB – величина

скорости мяча в точке В, которая является одновременно конечной для участка АВ и начальной для участка BD.

Система пяти уравнений (1) – (5) является замкнутой, так как содержит пять неизвестных величин: TB ,υB ,υBy , TD, T .

5*. Решим систему (1) – (5) относительно искомой величины T . Находя из (1) и (2) υB , подставляя (4) в (3) с учетом величины

υB , имеем систему трех уравнений с тремя неизвестными:
(6)	TB =	2g(H − h) g ,
	0 = h +TD			2g(H − h)cos 2α − gTD2 2 ,
(7)	0 = h +TD			2g(H − h)cos 2α − gTD2 2 ,
(5)	T = T		+T .
	B			D

Уравнение (7) является квадратным относительно TD .

Решение этого уравнения дает два корня, один из которых, отрицательный, мы отбрасываем (отрицательное время нас не интересует). В результате, подставляя в (5) TB из (6) и TD из

решения (7), имеем выражение для искомой величины T :

(8) T =	2g(H − h)	+	2g(H − h)cos 2α	+	2g(H − h)cos2 2α + 2gh	.
	g		g		g

В формуле (8) два последних слагаемых отражают время движения мяча на криволинейном участке траектории BD (см. рис.), причем, первое из них есть время движения материальной точки по восходящей ветви параболы, второе – время движения по нисходящей ветви параболы с учетом

-35 -

«ступеньки» высотой h. Таким образом, структура формулы

(8) учитывает движение материальной точки на трех участках траектории: прямолинейном, восходящей и нисходящей ветвях параболы, прекращая движение мгновенно в точке D.

6*. Проверка размерности единицы измерения полученной величины T сводится к проверке размерности одного из трех однотипных слагаемых конечного выражения (8):

[T ]=	м/с2 * м	=	м/с	= с.
	м/с2		м/с2

7*. Анализ задачи. Учитывая замечание к формуле (8), проанализируем ее для различных предельных случаев:

a) α =0, h=0, T =	3 2gH	– значение в три раза
	g

превышает ожидаемое, что и не удивительно, так как, упруго отскочив от поверхности, мяч продолжает двигаться прямолинейно (частный случай восходящей ветви параболы), а достигнув высшей точки, он еще должен попасть в точку D (частный случай

нисходящей ветви параболы);
b) H=0, T=0 – очевидный случай;
c) α = π 4, T =	2g(H − h)	+	2gh	– абсолютно
	g		g

верно, так как в этом случае отсутствует вертикальная составляющая скорости υB в момент времени T=0,

отсутствует движение по восходящей ветви параболы на участке BD и остается лишь кусочек движения по нисходящей ветви параболы, связанный со ступенькой h. Таким образом, на участке BD мяч как бы свободно падает с высоты h.

8*. Произведем расчет величины T :

	T =	2 * 9,8(10 − 2)	+ 2	* 9,8(10 − 2)	+
		9,8		9,8 * 2
+	2 * 9,8(10 − 2)* 0,25 + 2 * 9,8 * 2 ≈ 1,28			+ 0,64 + 0,90 ≈ 2,8(c).
	9,8

- 36 -

9*. Ответ:

T =

2g(H − h)

2g(H − h)cos 2α

2g(H − h)cos2 2α + 2gh

≈ 2,8c.

***************

Задача 3

h = 20 м брошено

мачты

высотой

тело

начальной

скоростью

υ0 = 30 м/с под углом α = 45° к горизонту.

Построить

траекторию

движения тела.

1*. Дано:

Решение.

2*.

h = 20 м,

v0x

v0y

α = 45°=π/4,

v0x

υ0 = 30 м/с,

g = 9,8 м/с2.

B X

3*.

Анализ

задачи.

Выберем прямоугольную

систему координат с началом отсчета в точке 0 (см. рис. ниже). Часы включаем в момент начала движения тела с высоты h. Очевидно, тело можно считать материальной точкой. Движение материальной точки является криволинейным и

равнопеременным, причем на участке АС				–
равнозамедленным,	на	участке	СВ	–

равноускоренным.

На всей траектории будем использовать принцип


независимости	движений:		равномерное		и
прямолинейное по оси OX, происходящее с
начальной скоростью		υ0x =υ0 cosα , и		свободное
падение по	оси OY	с начальной		скоростью
υ0 y =υ0 sinα .	Для	построения		траектории

движения необходимо найти аналитическое выражение, то есть зависимость y = y(x), так как

движение является плоским.

- 37 -

4*. Составим полную систему уравнений. Движение тела описывается законом равнопеременного движения по траектории AСB, по оси ОY:

			+υ0 yt + at		2	2,	y0 = h,	υ0 y =υ0 sinα,		a = −g,
y(t) = y0			+υ0 yt + at			2,	y0 = h,	υ0 y =υ0 sinα,		a = −g,
υ	y	(t) =υ	0 y	+ at,			a = −g;
	y		0 y
по оси OX:			x(t) = x0 +υ0 xt, x0 = 0,					υ0x =υ0 cosα.
			x(t) = x0 +υ0 xt, x0 = 0,					υ0x =υ0 cosα.
	Сведем записанные уравнения в систему:
				(1)			y(t) = h +υ0yt − gt2		2 ,
							υ0y =υ0 sinα,
				(2)			υ0y =υ0 sinα,
							x(t) =υ0xt,
				(3)			x(t) =υ0xt,
							υ0x =υ0 cosα,
				(4)			υ0x =υ0 cosα,
							y = y( x).
				(5)			y = y( x).
	Система пяти уравнений (1) – (5) является замкнутой, так
как содержит пять неизвестных величин: x,									y, t , υ0x , υ0y . Для

нахождения искомой зависимости (для написания уравнения траектории y = y(x) необходимо в системе уравнений (1) – (4)

исключить время t.

5*. Подставляя (2) в (1) и (4) в (3), имеем систему трех уравнений с тремя неизвестными величинами:

(6)	y(t) = h +υ0 sinα t − gt2						2,
	x(t) =υ0 cosα t,
(7)
(5)	y = y( x).

Выражаем величину t из (7) и подставляем ее в (6), получаем
искомую зависимость y = y(x):			g
(8)	y( x) = −					x2 + xtgα + h.
			2υ02 cos2		α

6*.Уравнение (8) является, очевидно, уравнением параболы
	a = −		g		b = tgα		и c = h. Для
с коэффициентами				,
		2υ02 cos2 α

построения графика полученной функции необходимо уравнение

(8) сделать приведенным для числовых величин (подставить

- 38 -

числовые данные исходных величин), а для этого, в свою очередь, необходимо проверить размерность каждого слагаемого уравнения (8), которая должна иметь размерность длины [L] и соответствующую единицу измерения – метр. Таким образом, проверка размерности сводится к установлению единицы измерения первого слагаемого правой части уравнения (8). Второе и третье слагаемые, бесспорно, имеют размерность длины:

[a * x2 ]= м/ с2 *м2 = м.

м2 / с2

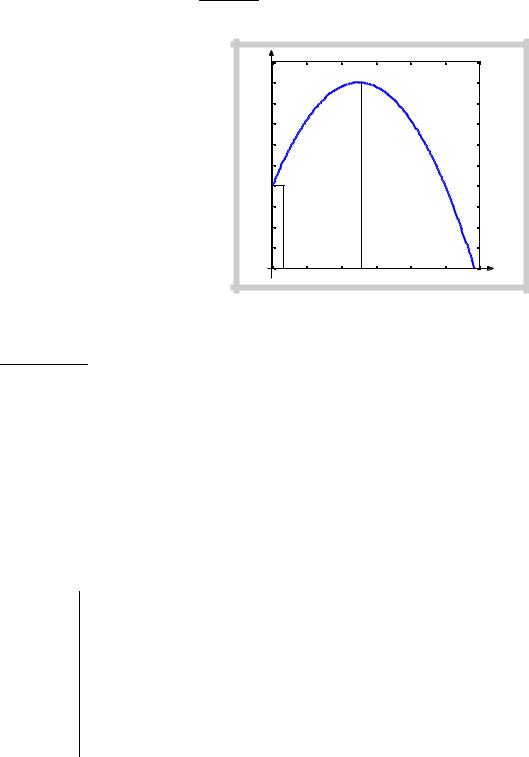
8*.		Подставляя			Y,м		Y=-0,01x2 +x+20
исходные	данные			в	45
уравнение	(8),	получаем			40
приведенное		уравнение			35
искомой траектории:					30		H
					30
y(x)= −0,01x2 + x + 20 =					25
y(x)= −0,01x2 + x + 20 =				,	20
= −0,01(x − 50)2 + 45				,	15
					15	h
					10	h
					5
график	функции		которой		0	20	40	60 80 100	L	X,м
приведен на рисунке.
9*.Ответ:		2 + xtgα + h = (− 1,0 10−2 x2 + 1,0x + 2,0 101 )м.
	g
y( x) = − 2υ02 cos2 α x
			***************
Задача 4		R = 0,1 м вращается
Диск	радиусом	R = 0,1 м вращается				так,	что	зависимость	линейной

скорости точек, лежащих на ободе диска, от времени имеет вид

υ = 3t + t 2 (м/c). Определить угол α , который образует вектор полного

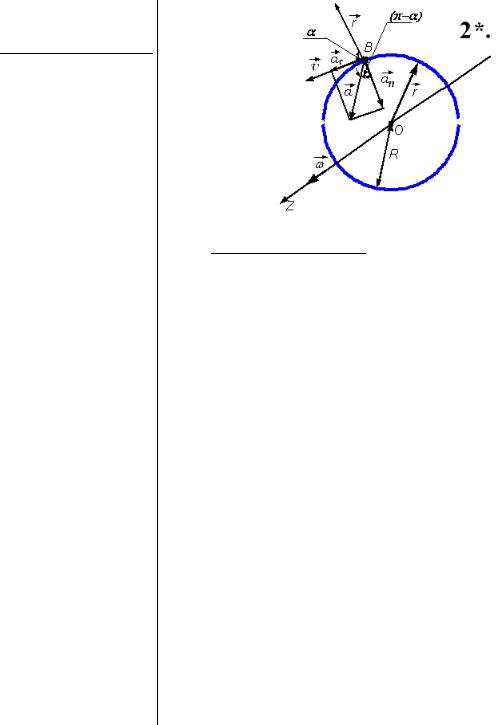
ускорения с радиус-вектором r , направленным из центра диска O в точку наблюдения (см. рис.) через T = 0,2 с после начала движения.

1*. Дано: Решение.

R = 0,1 м,

υ = 3t + t 2 (м/c)

- 39 -

T = 0,2 с.

α - ?

3*. Анализ задачи. Ось OZ неподвижной системы координат XOYZ совместим с неподвижной осью вращения диска (см. рис.). Радиус-вектор r этой системы координат отслеживает поведение рассматриваемой (произвольной) точки В, находясь в плоскости диска. Часы синхронизованы с моментом начала движения указанной точки В.

Движение точки В не подчиняется какомулибо хорошо изученному конкретному закону. Однако ее движение подчиняется общим законам поступательного и вращательного движений, поэтому справедливы соотношения между кинематическими характеристиками поступательного и вращательного движений.

Искомый угол α обозначен на рисунке. Как следует из того же рисунка, проще найти тангенс угла (π −α) как отношение тангенциального ускорения к нормальному. Затем из π вычесть арктангенс правой части.

4*. Составим полную систему уравнений:

(1)(2)

(3)

(4)

(5)

υ(t) = 3t + t2 , aτ = dυ(t)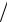dt , an =υ(T )2 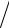R,

tg(π −α)= aτ (T )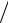an (T ),

T = t.

- 40 -

<<< < Предыдущая 1 2 34 / 224 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
24.09.2019234.97 Кб4естествознание экзамен.docx
#
06.11.201859.39 Кб1жаргон.doc
#
19.09.20193.05 Mб1Задание 1 часть_В1-В34.docx
#
17.03.201650.22 Кб11Задание1.docx
#
17.03.2016172.54 Кб37Задачи_БФО.doc
#
17.03.20162.49 Mб89Задачник по физике.pdf
#
27.11.201983.37 Кб7Западноевропейское общество и государство X-XI...docx
#
12.11.2019149.5 Кб2Зачетное задание по НИРс2.doc
#
06.05.201973.22 Кб3зернов.doc
#
17.07.20191.46 Mб2ИВТ_РГР3.doc
#
15.11.2019116.74 Кб3ИГПЗС (Огнев).doc