
Задачник по физике
.pdf
Joz и Loz −момент инерции и проекция на ось OZ момента импульса
тела, вращающегося относительно неподвижной оси OZ, ε −угловое ускорение тела.
19. Закон сохранения момента импульса Loz замкнутой
системы тел, вращающихся вокруг неподвижной оси
OZ:
(4.27) Loz = Jozω = const ,
где Joz − момент инерции системы тел относительно оси OZ, ω −угловая скорость вращения тел системы вокруг оси OZ.
***** §4 *****
§5. Основы молекулярной физика и термодинамики
1. Количество вещества системы (тела) ν :
(5.1) ν = N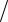 NA ,
NA ,
где N −число структурных элементов (молекул, атомов, ионов и т.п.), составляющих систему (тело),
NA − постоянная Авагадро.
2. Молярная масса вещества M :
(5.2) M = m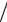 ν ,
ν ,
где m −масса однородной системы (тела),
ν−количество вещества этой системы.
3.Относительная молекулярная масса вещества Mr :
n
(5.3) Mr = ∑ni Ar,i ,
i=1
где ni −число атомов i −го химического элемента, входящих в состав молекулы данного вещества,
Аr,i −относительная атомная масса i −го химического элемента, определяемая по таблице Д.И. Менделеева.
4. Связь молярной массы М с относительной молекулярной массой вещества Mr в системе СИ:
(5.4) M = Mr k ,
где k =10−3 кг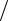 моль.
моль.
- 21 -
5. Количество вещества смеси газов μ:
|
n |
1 |
n |
n |
||
(5.5) |
μ = ∑νi = |
∑Ni = ∑ |
mi |
, |
||
|
|
|||||
|
i=1 |
NA i=1 |
i=1Mi |
|||
где νi , Ni , mi , Mi −соответственно |
количество вещества, число |
|||||
молекул, масса, молярная масса i −го компонента смеси.
6.Уравнение состояния идеального газа (уравнение Менделеева-Клапейрона):
(5.6) pV = Mm RT =νRT ,
где m и M −масса и молярная масса газа, R −молярная газовая постоянная,
T−термодинамическая температура,
ν−количества вещества.
7.Изопроцессы – частные случаи уравнения состояния идеального газа:
а) изотермический процесс - Т = const, m = const (закон
Бойля-Мариотта)
(5.7) pV = const ;
б) изобарный процесс - p = const, m = const (закон Гей-
Люссака)
|
(5.8) |
|
V |
= const ; |
|||||||
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
в) изохорный |
процесс |
|
- |
V = const, m = const (закон |
|||||
|
|
Шарля) |
|
|
|
p |
|
|
|
|
|
|
(5.9) |
|
|
= const ; |
|||||||
|
|
T |
|||||||||
|
|
|
|
|
|
|
|
|
|||
|
|
г) объединенный газовый закон - m = const |
|||||||||
|
(5.10) |
|
|
pV |
= const , |
||||||
|
|
|
|
||||||||
|
|
p , V и T −давление, |
|
|
|
T |
|
|
|
|
|
где |
|
объем |
|
и |
термодинамическая температура |
||||||
идеального газа, измеренные в определенной точке процесса. |
|||||||||||
8. |
Закон Дальтона: |
|
|
|
|
|
|
|
|
n |
|
|
( |
|
) |
|
p |
= |
|||||
|
5.11 |
|
|
|
|
∑ pi , |
|||||
где |
p −давление смеси газов, |
|
|
|
|
|
|
|
i =1 |
||
|
|
|
|
|
|
|
|
||||
pi −парциальное давление i -го компонента смеси,
- 22 -

n−число компонентов смеси.
Парциальным называется давление такого газа, которое производил бы этот газ, если бы только он один находился в сосуде, занятом смесью.
9. Концентрация молекул n:
(5.12) n = VN = ρMNA ,
где N −число молекул, содержащихся в рассматриваемой системе, V −объем системы,
ρ −плотность вещества,
M−молярная масса системы,
NA −постоянная Авогадро.
***************
10. Основное уравнение кинетической теории газов:
(5.13) p = 2 3 n < εn >,
где p −давление, создаваемое молекулами системы,
n−концентрация молекул системы,
<εn > −средняя кинетическая энергия поступательного движения одной
молекулы.
11. Средняя кинетическая энергия поступательного движения молекулы < εn > в расчете на одну степень
свободы:
(5.14) < εn >= 12 kT ,
где k −постоянная Больцмана,
T −термодинамическая температура.
12. Средняя полная кинетическая энергия молекулы < εi >:
(5.15) < εi >= i 2 kT ,
где i −число степеней свободы молекулы, k −постоянная Больцмана,
T −термодинамическая температура.
13. Зависимость давления газа р от концентрации молекул
n и термодинамической температуры T : |
|
(5.16) |
p = nkT , |
где k − постоянная Больцмана.
14. Скорости молекул:
а) средняя квадратичная <υкв >
- 23 -
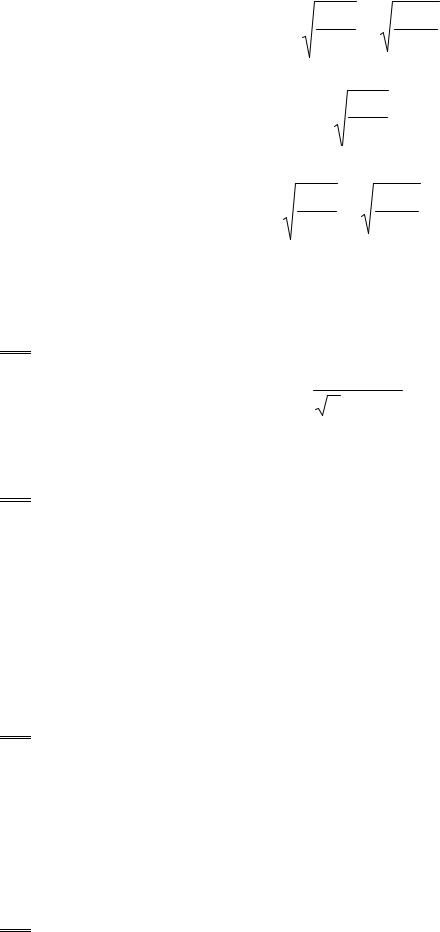
(5.17) |
<υкв >= |
3kT = |
3RT |
; |
|
б) средняя арифметическая |
m1 |
|
M |
|
|
<υ > |
|
|
|||
(5.18) <υ >= |
8kT |
; |
|
||
|
|
|
πm |
|
|
в) наиболее вероятная υв |
|
1 |
|
|
|
|
|
|
|
||
(5.19) |
υв = |
2kT = 2RT , |
|
||
|
|
m1 |
|
M |
|
где m1 и M −масса и молярная масса одной молекулы,
k − постоянная Больцмана,
R −молярная газовая постоянная,
T −термодинамическая температура.
15. Средняя длина свободного пробега молекул:
(5.20) < l >= |
1 |
, |
2 πd 2n |
||
где d − эффективный диаметр молекулы, |
|
|
n − концентрация молекул газа. |
|
|
***************
16. Удельные теплоемкости газа при постоянном объеме сV и постоянном давлении c p :
(5.21) |
c |
|
= |
|
i |
|
R |
, |
|
|
|||
|
|
|
|
|
|||||||||
|
|
V |
2 |
|
M |
|
|
||||||
|
|
|
|
|
|
|
|||||||
(5.22) |
c |
p |
= |
i + 2 |
|
R |
, |
|
|||||
|
|
|
|||||||||||
|
|
|
|
|
|
|
2 M |
|
|
||||
где i − число степеней свободы молекулы газа, |
|
|
|||||||||||
R −молярная газовая постоянная, |
|
|
|
|
|
|
|
|
|
|
|
||
M −молярная масса молекулы. |
|
|
|
|
|
|
|
|
|
|
|
|
|
17. |
Уравнение Майера и связь молярной C и удельной |
c |
|||||||||||
|
теплоемкостей: |
|
|
|
|
|
|
|
|
|
|
|
|
|
(5.23) |
Сp − СV = R, |
|
||||||||||
|
(5.24) |
С = cM , |
, |
|
|||||||||
|
|
|
|||||||||||
где C p и CV −молярные теплоемкости |
при |
постоянном давлении |
и |
||||||||||
объеме,
R −молярная газовая постоянная.
18. Внутренняя энергия идеального газа U :
- 24 -

(5.25) U = |
m |
|
i |
RТ = |
m |
C Т, |
|
|
|
||||
|
M 2 |
M V |
||||
где m и M −масса и молярная масса газа, |
|
|
||||
i − число степеней свободы молекул газа, |
|
|
||||
R −молярная газовая постоянная,
T −термодинамическая температура.
19. Первое начало термодинамики для элементарного количества теплоты δQ , элементарной работы δA и
бесконечно малого изменения внутренней энергии dU :
(5.26) δQ = dU +δA.
20. Работа расширения идеального газа А: а) при изобарном процессе (р=const)
V2
(5.27) A = ∫ pdV = р(V2 −V1 );
V1
б) при изотермическом процессе (Т=const)
|
|
|
|
|
|
|
V |
|
|
|
m |
|
RT lnV2 ; |
|
|
|
|
|
||||
|
|
(5.28) |
|
A = ∫2 pdV = |
|
|
|
|
|
|
||||||||||||
|
|
M |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
V |
|
|
|
|
|
|
V1 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в) при адиабатном процессе (δQ = 0) |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
RT1 |
|
m |
|
|
|
γ −1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
(5.29) |
A = − |
U = − |
C |
(T −T )= |
|
|
1 |
− V1 |
|
|
|
, |
||||||||||
|
γ −1 |
|
|
|||||||||||||||||||
|
|
|
|
|
M |
V |
2 |
|
1 |
|
|
M |
V |
|
|
|
|
|||||
где V1 и V2 −начальный и конечный объёмы газа, |
|
|
2 |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||
р−давление газа, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
m и M −масса и молярная масса газа, |
|
|
|
|
|
|
|
|
|
|
||||||||||||
R −молярная газовая постоянная, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Т1 и T2 −начальная и конечная термодинамическая температура газа, |
||||||||||||||||||||||
γ = ср |
сV −показатель адиабаты, |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
U −изменение внутренней энергии системы, |
|
|
|
|
|
|
|
|||||||||||||||
CV −молярная теплоемкость при постоянном объеме. |
|
|
|
|
|
|||||||||||||||||
21. |
Уравнения |
Пуассона, |
связывающие |
параметры |
||||||||||||||||||
|
идеального газа при адиабатном процессе (δQ = 0): |
|
|
|||||||||||||||||||
|
|
|
|
(5.30) |
|
pV γ |
= const, |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
γ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(5.31) |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
pT |
1−γ |
= const, |
|
|
|
|
|
|
|
|||||||||
1
(5.32) VT γ −1 = const,
- 25 -
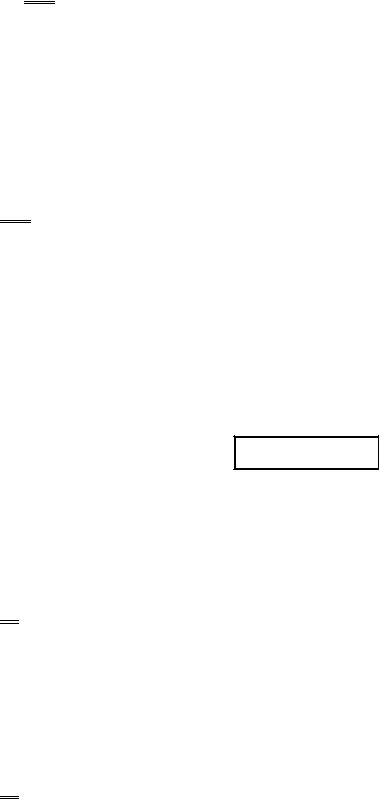
где p , V и T − давление, объем и температура газа, γ = ср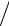 сV −показатель адиабаты.
сV −показатель адиабаты.
22. Термический коэффициент полезного действия η
обратимого цикла Карно:
(5.33) η = |
Q1 − Q2 |
= T1 −T2 |
, |
|
Q |
T |
|
|
1 |
1 |
|
где Q1 − теплота, полученная рабочим телом от нагревателя,
Q2 − теплота, переданная рабочим телом холодильнику,
T1 и T2 − термодинамические температуры нагревателя и холодильника.
23. Изменение энтропии S при равновесном переходе из состояния 1 в состояние 2:
(5.34) S = S |
2 |
− S |
= |
2 |
δQ |
= |
2 dU +δA |
, |
|
|
1 |
|
∫ |
T |
|
∫ |
T |
|
|
|
|
|
|
1 |
|
1 |
|
||
где δQ − элементарное изменение количества теплоты,
δA − элементарная работа, совершаемая газом против внешних сил, dU − бесконечно малое изменение внутренней энергии газа,
T −термодинамическая температура газа.
***** §5 *****
§6. Свободныенезатухающиеколебанияиупругие волны. Специальнаятеорияотносительности
1. Кинематическое уравнение гармонических колебаний материальной точки:
(6.1) х(t)= Аcos(ωt +ϕ),
где x(t)− смещение из положения равновесия,
А−амплитуда колебаний,
ω−циклическая частота колебаний,
ϕ−начальная фаза колебаний.
2. |
Скорость |
υ и |
ускорение а МТ, совершающей |
|
гармонические колебания: |
||
|
(6.2) |
υ(t )= x& |
(t )= −Аωsin(ωt +ϕ), |
|
(6.3) |
a(t )=υ&(t )= &x&(t)= −Аω2 cos(ωt +ϕ). |
|
|
|
|
- 26 - |
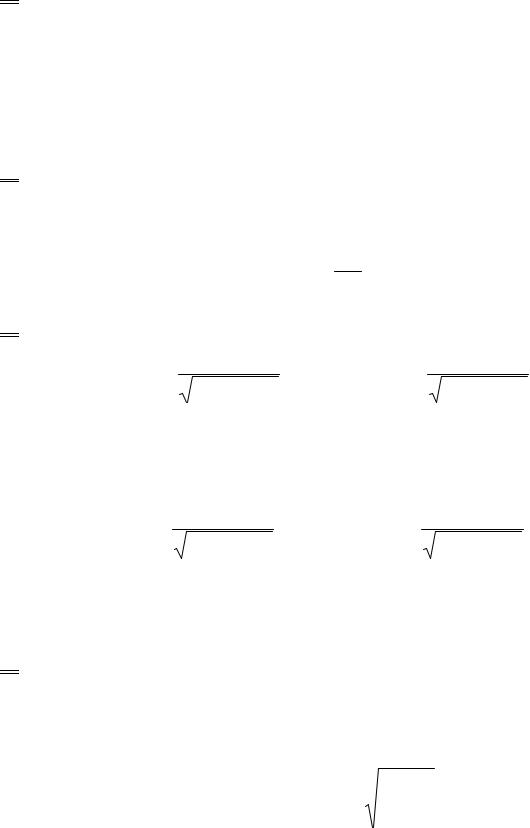
3. Решение волнового уравнения – плоская бегущая монохроматическая волна:
|
|
x |
|
(6.4) |
y(t, x)= Аcosω t − |
|
, |
|
|||
|
|
υ |
|
где y − смещение точки среды с координатой х в момент времени t,
А−амплитуда колебаний волны,
υ−скорость распространения колебаний в среде.
4. Связь разности фаз ϕ колебаний с расстоянием х
между точками среды, отсчитанным в направлении распространения колебаний:
(6.5) ϕ = 2λπ х,
где λ − длина волны.
5. Преобразования Лоренца для координат и времени:
|
х − ut |
|
, |
|
|
х′ + ut |
′ |
, |
||||||
х′ = |
1 − u2 / c2 |
х = |
1 − u2 / c2 |
|||||||||||
|
|
|
|
|||||||||||
y′ = y, |
|
|
|
|
y′ = y, |
|
|
|
|
|
||||
(6.6) z′ = |
z, |
|
|
|
и (6.7) |
z′ = z, |
|
|
|
|
|
, |
||
|
|
ux |
|
|
|
|
|
|
|
ux |
′ |
|
|
|
|
|
|
|
|
|
′ |
|
|
|
|||||
|
|
|
|
|
|
|
|
|||||||
t − c |
2 |
|
|
|
t |
+ |
c2 |
|
|
|
||||
|
|
; |
|
|
|
|
, |
|||||||
t′ = |
1 − u2 |
/ c2 |
t = |
1 − u2 / c2 |
||||||||||
|
|
|
|
|
||||||||||
где где c – скорость света в вакууме, а |
оси |
декартовых координат |
||||||||||||
неподвижной Σ и движущейся Σ′ инерциальных систем попарно параллельны ( u −скорость движения Σ′ относительно Σ).
6. Преобразования Лоренца для скоростей:
(6.8) υ′x′ = dx′ |
= |
υx − u |
, |
|
|
|||||||||
|
|
|||||||||||||
|
dt |
′ |
|
1 − |
uυx |
|||||||||
|
|
|
|
|
c2 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dy′ |
|
υy |
|
1 − |
u2 |
|
|||||||
(6.9) υ′y′ = |
|
|
c2 |
, |
||||||||||
= |
|
|
|
|
|
|||||||||
dt′ |
|
|
|
|
|
|
||||||||
|
|
1 |
− |
|
uυx |
|
||||||||
|
|
|
|
c2 |
||||||||||
|
|
|
|
|
|
|
|
|||||||
- 27 -
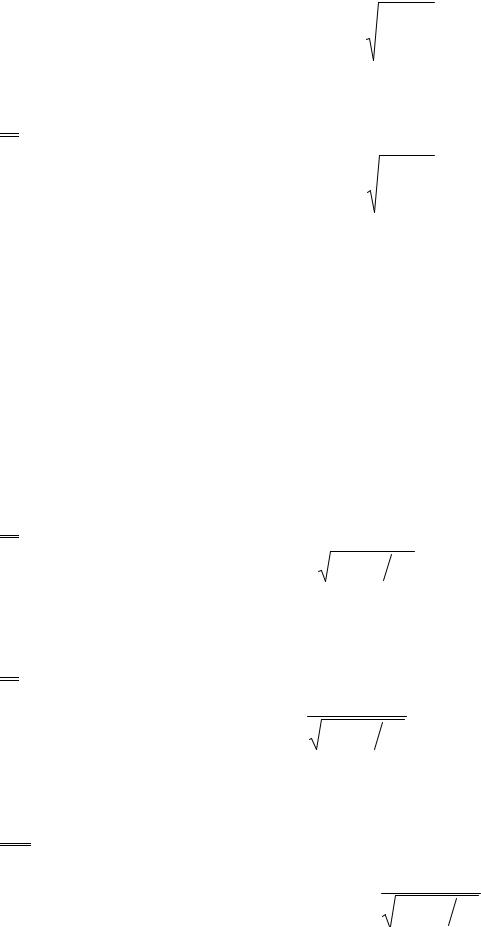
|
|
dz′ |
υz |
1 |
− |
u2 |
|
||||||
(6.10) |
υz′′ = |
c |
2 |
. |
|||||||||
= |
|
|
|
|
|||||||||
dt′ |
|
|
uυx |
|
|||||||||
|
|
1 |
− |
|
|
|
|
||||||
|
|
|
|
c2 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|||
7. Преобразования Лоренца для ускорений:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u |
2 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
dυ′x′ |
|
|
|
|
|
1 |
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
(6.14) |
|
|
|
|
|
|
|
|
|
|
|
c2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
a′x′ = |
dt′ |
|
|
= ax |
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
uυx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u2 |
|
|
|
|
||||||||
|
|
|
|
|
|
dυ′ |
|
|
|
|
uυx |
|
|
|
uυ |
|
|
|
|
|
|
|
|
|
1 − |
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
c |
2 |
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
(6.15) |
′ |
|
y′ |
|
|
|
|
|
|
|
|
|
|
ax |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
1 − |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 , |
|||||||||||||||||||||
|
|
|
ay′ = |
|
dt′ |
= |
|
c |
2 |
|
ay + |
|
c |
|
|
|
|
|
|
|
uυ |
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 − |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c2 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
dυ′′ |
|
|
|
|
uυ |
|
|
|
|
uυ |
|
|
|
|
|
|
|
|
|
|
1 − |
|
u2 |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
(6.16) |
|
|
|
x |
|
|
z |
|
|
|
|
|
|
|
|
c |
2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
a′z′ = |
|
z |
|
= |
1 |
− |
|
|
|
az |
+ |
|
|
|
|
ax |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
||||||||||||||
|
|
|
|
dt′ |
|
c2 |
|
c2 |
|
|
|
|
|
uυ |
|
|
|
3 |
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
− |
x |
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
8. |
|
Лоренцево сокращение длины: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c2 |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
(6.17) |
L = L |
|
1 − u2 |
c2 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
L0 − длина покоящегося |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
скоростью u |
|||||||||||||||||||
|
где |
стержня в |
движущейся |
со |
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
системе координат Σ′ относительно неподвижной Σ. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
9. |
|
Лоренцево замедление времени: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
(6.18) |
τ = |
|
|
|
τ0 |
|
|
c2 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
1 − u2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
где τ0 − промежуток времени между двумя событиями в одной и той же
неподвижной относительно Σ′ точке пространства, измеренный по часам системы Σ′ ( u −скорость движения Σ′ относительно Σ).
10. Основной закон релятивистской динамики:
|
dpr |
r |
|
d |
m υr |
|
|
|
r |
|
||
(6.19) |
|
= F , |
или |
|
|
0 |
2 |
|
2 |
|
= F |
, |
|
|
|
||||||||||
|
dt |
|
|
|
|
1 −υ |
c |
|
|
|
||
|
|
|
dt |
|
|
|
|
|
||||
где p − импульс материальной точки,
F− главный вектор внешних сил, действующих на точку.
-28 -

11. Закон взаимосвязи массы и энергии:
(6.20) W = mc2 = m0c2
где W − полная энергия тела,
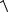 1 −υ2
1 −υ2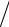 c2
c2
m и m0 − релятивистская масса и масса покоя тела.
***** §6 *****
- 29 -
|
|
§7. Примерырешенияиоформлениязадач |
|
|
|||||||||
|
|
Задача 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
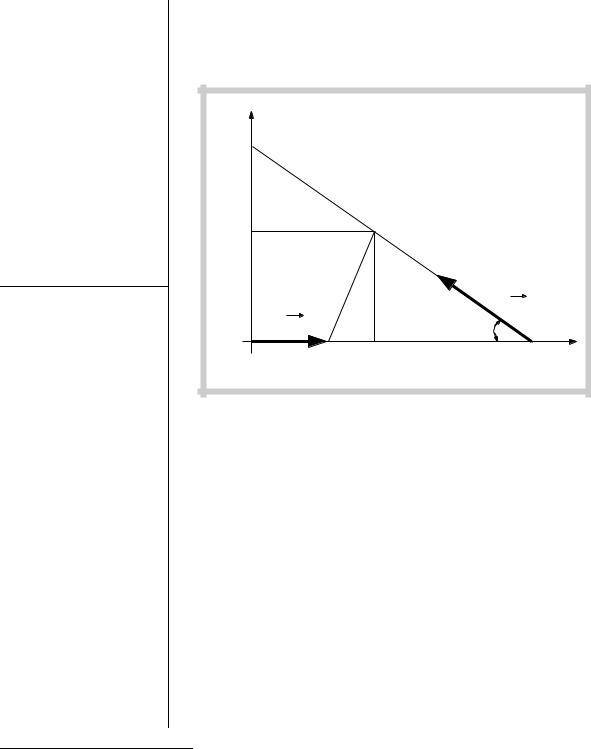
Точка P1 движется из А по направлению к В равномерно со скоростью |
|||||||||||
|
|
υ1 = 5 м/с. Одновременно точка P2 движется из В по направлению к С |
|||||||||||
|
|
равномерно |
со скоростью υ2 = 8 м/с (см. рис. ниже). |
Расстояние |
АВ |
||||||||
|
|
= L = 1200 см. Угол АВС равен α = 60°. Определить момент времени |
|||||||||||
|
|
Tmin , когда расстояние r между точками P1 и P2 |
будет минимальным. |
||||||||||
13*. Дано: |
3*. |
|
|
Решение. |
|
|
|
|
|
||||
υ1 =5 м/c, |
Анализ |
задачи. |
Движение |
каждой |
из |
||||||||
материальных |
точек |
по |
своей |
траектории |
|||||||||
υ2 =8 м/c, |
|
Y |
|
|
|
|
|
|
2* |
|
|
||
|
C |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
α = 60º=π/3, |
|
|
|
|
|
|
|
|
|
|
|
||
L = 1200 см= |
|
Y2(t). |
|
|
.K |
|
|
|
|
|
|
||
|
=12 м. |
|
|
|
r(t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
- ? |
|
A |
v |
P1 |
.H |
P2 |
v2 |
B |
|
|
|
|
|
α |
|
|
|||||||||
min |
|
|
0 |
1 |
.M |
|
X |
|
|||||
|
|
|
|
|
X1(t) X2(t) |
|
|
L |
|
||||
|
|
|
является |
равномерным |
прямолинейным. |
||||||||
|
|
|
Расстояние KM между точками P1, P2 (см. |
||||||||||
|
|
|
рис.) изменяется с течением времени t. |
||||||||||
|
|
|
Минимальное |
|
расстояние |
|
между |
||||||
|
|
|
рассматриваемыми точками r(t) (не путать с |
||||||||||
|
|
|
радиус-вектором r (t) !) будет зависеть от |
||||||||||
|
|
|
начальных условий движения (υ1,υ2, α, L – |
||||||||||
|
|
|
const) и от момента времени Tmin , когда |
||||||||||
|
|
|
функция r(t) будет иметь наименьшее |
||||||||||
|
|
|
значение. |
Следовательно, |
наша |
задача |
|||||||
|
|
|
сводится к написанию функции r = r(t) в |
||||||||||
|
|
|
общем виде и отысканию ее экстремума, то |
||||||||||
|
|
|
есть |
вычислению |
первой |
производной |
|
по |
|||||
3При оформлении задач каждый этап рекомендуется оформлять цифрой со звездочкой
-30 -
