
Zhilin_Fundamental_Laws_Book
.pdf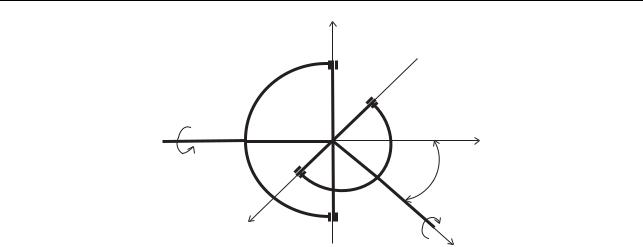
152 |
Глава 3. Кинематика: спинорные движения |
|||
|
|
|
k |
|
|
|
|
B |
|
|
|
|
A1 |
|
|
ù1 |
|
O |
|
|
|
|
|
|
|
C |
|
|
j |
|
|
A |
D |
è |
|
|
|
|
|
|
i |
|
|
ù3 |
|
|
B1 |
|
|
|
|
|
n |
|
|
|
|
|
|
|
Рис. 3.12. Шарнир Гука |
|
||
возможно. В таких случаях необходимо сначала установить какие необходимые ограничения налагаются на тензор поворота. Только после этого следует принимать решение о выборе представления тензора поворота. Шарнир Гука является подходящей иллюстрацией сказанного.
Шарнир Гука используется для передачи вращения от одного вала к другому. Причем оба вала расположены в одной плоскости, но составляют угол θ между собой. Схематическое изображение шарнира Гука представлено на рис. 3.12, котором векторы i, j, k образуют правую ортонормированную тройку. В отсчетном положении входной вал CO расположен вдоль вектора j. Вилка CB входного вала расположена в плоскости, натянутой на векторы j и k. Выходной вал OD расположен вдоль вектора n : | n| = 1, который также расположен в вертикальной плоскости, натянутой на j, k. Входной и выходной валы пересекаются в точке 0, которая остается неподвижной при вращении валов. Диаметр OA вилки DA выходного вала в отсчетном положении расположен вдоль вектора i. Ось выходного вала, т.е. вектор n, ортогональна диаметру OA вилки DA. Входной вал вращается с угловой скоростью ω1, что заставляет вращаться выходной вал с угловой скоростью ω3.
ω1 = ω1 j, ω3 = ω3 n, |
(3.19.1) |
где j · n = cos θ = const.
Соединение входного и выходного валов осуществляется с помощью крестовины AOB, которая считается абсолютно твердым телом. Входной вал вращает диаметр BB1 крестовины. В результате начинает вращаться диаметр AA1 крестовины, что приводит к вращению выходного вала. Таким образом, шарнир Гука представляет собой сочленение трех абсолютно твердых тел: входного вала с вилкой BCB1 (тело 1), крестовины ABA1B1 (тело 2) и выходного вала с вилкой ADA1 (тело 3). Все три тела имеют одну и ту же неподвижную
3.19. Шарнир Гука |
153 |
точку O. Понятно, что движение крестовины и выходного вала полностью определяется геометрическими факторами (в частности, углом θ ) и поворотами входного вала. Требуется определить угловую скорость выходного вала, а также тензор поворота крестовины P2 и угловую скорость крестовины.
Введем обозначения: P1, P2, P3 суть тензоры поворота входного вала, крестовины и выходного вала соответственно. Оси поворота входного и выходного валов заданы и фиксированы
|
P1 = Q(ϕ j), |
P3 = Q(ψ n), |
(3.19.2) |
|
причем угол поворота входного вала известен |
|
|||
ω1 |
= ω1 j = ϕ˙ j |
|
ϕ(t) = t ω1(τ)dτ. |
(3.19.3) |
|
|
0 |
|
|
Угол поворота выходного вала ψ и его угловая скорость подлежат опре- |
||||||||||
делению. Будем считать, что начало в системе отсчета выбрано в точке O. |
||||||||||
Тогда в отсчетном положении материальные векторы OA и OB совпадают с |
||||||||||
векторами |
OA |
|
|
l , |
OB |
|
−−→ |
−→ |
(3.19.4) |
|
|
rA = |
rB = |
l . |
|
||||||
|
−−→ |
|
i |
−→ |
k |
|
||||
В актуальном положении имеем |
|
OB |
|
|
|
|
||||
|
|
OA |
|
|
|
|
|
|
||
|
|
−−→ |
RA, |
−→ |
RB. |
|
|
(3.19.5) |
||
Для вектора RB в соответствии с основным уравнением кинематики имеем |
||||||||||
равенство |
|
RB = P1 · rB = P2 · rB. |
|
|
|
|||||
|
|
|
|
(3.19.6) |
||||||
|
|
|
|
|
|
|
|
|
OB |
|
Это равенство справедливо в силу того, что материальный вектор − |
одно- |
|||||||||
|
|
|
|
|
|
|
|
|
|
(3.19.2) |
временно принадлежит как входному валу, так и крестовине. С учетом→ |
||||||||||
и (3.19.4) равенство (3.19.6) можно переписать в виде |
|
|
||||||||
|
Q(ϕ j) · k = P2 · k |
j · P2 · k = 0. |
|
(3.19.7) |
||||||
Получили первое ограничение, которому должен удовлетворять тензор по-
ворота P2. Аналогичные рассмотрения применительно к материальному век-
−−→
тору OA дают
RA = P3 · rA = P2 · rA Q(ψ n) · i = P2 · i. |
(3.19.8) |
Умножая скалярно последнее равенство на n и учитывая, что n · i = 0, получаем второе ограничение на тензор P2
n · P2 · i = 0. |
(3.19.9) |
154 |
Глава 3. Кинематика: спинорные движения |
Таким |
образом, тензор поворота P2 удовлетворяет двум ограничениям |
(3.19.7) и (3.19.9), которые должны выполняться при всех возможных поворотах крестовины. Всякий тензор поворота зависит от трех параметров. На эти три параметра, какие бы они не были, наложено два ограничения. Следовательно, только один из упомянутых параметров остается независимым, а два другие могут быть выражены через него. Ограничение (3.19.7) показывает, что тензор P2 является двухпараметрическим. Будем искать этот двухпараметрический тензор в следующем виде
P2 = Q(α j) · Q(β k). |
(3.19.10) |
Легко убедиться, что при любых значениях параметров α и β ограничение (3.19.7) тождественно выполнено. Потребуем, чтобы тензор (3.19.10) удовлетворял условию (3.19.9).
n · Q(α j) · Q(β k) · i = 0. |
(3.19.11) |
Вспоминая, что
Q(β k) = (1 − cos β) k k + cos β E + sin β k × E,
получаем
Q(β k) · i = cos β i + sin β k × i = cos β i + sin β j.
Подставляя это соотношение в (3.19.11) и проводя аналогичные вычисления, получаем равенство
n · Q(α j) · (cos β i + sin β j) = cos β sin α sin θ + sin β cos θ = 0
или в другой форме |
|
tg β = − tg θ sin α. |
(3.19.12) |
Итак, тензор P2 имеет вид (3.19.10), где параметры α и β связаны соотношением (3.19.12). Теперь мы должны вернуться к равенству (3.19.6) и первому из равенств (3.19.8). Дифференцируя (3.19.6) по времени и исключая производные от тензоров поворота посредством соответствующих уравнений Пуассона, получаем
ϕ˙ j × RB = ω2 × RB. |
|
Умножая это равенство векторно на RB, получаем |
|
ω2 = ϕ˙ j + RB(ω2 · RB) l−2, |
(3.19.13) |
где
l2 = RB · RB, RB · j = 0.
3.19. Шарнир Гука |
155 |
Дифференцируя (3.19.8) по времени, получаем аналогичное равенство для
вектора RA |
|
|
|
|
|
˙ |
− RA(ω2 |
· RA) l |
−2 |
. |
(3.19.14) |
ψ n = ω2 |
|
Равенство (3.19.13) позволяет вычислить угловую скорость ω2, а равенство (3.19.14) позволяет найти угловую скорость выходного вала
˙ |
· n. |
(3.19.15) |
ψ = ω2 |
Угловая скорость ω2, отвечающая повороту (3.19.10), вычисляется по фор-
муле |
|
|
˙ |
|
|
|
|
|
|
(3.19.16) |
|
|
ω2 = α˙ j + β Q(α j) · k. |
|
|||
Сравнивая (3.19.13) и (3.19.16), получаем |
|
|
|||
α˙ |
˙ |
· k = ϕ˙ j + RB(ω2 · RB)l |
−2 |
. |
|
j + βQ(α j) |
|
||||
Проецируя это равенство на вектор j, получаем |
|
|
|||
|
α˙ = ϕ˙ |
|
α(t) = ϕ(t). |
|
(3.19.17) |
Здесь и далее мы принимаем |
начальные условия в виде |
|
|||
|
|
|
|
||
|
α(0) = β(0) = ϕ(0) = ψ(0) = 0. |
|
(3.19.18) |
||
Итак, угол поворота α(t) оказался равным углу поворота ϕ(t) входного
˙ |
|
|
|
|
вала. Чтобы найти β достаточно продифференцировать (3.19.12) по времени. |
||||
Тогда получим |
|
|
|
|
˙ |
+ tg |
2 |
β) = −ϕ˙ tg θ cos ϕ. |
(3.19.19) |
β(1 |
|
|||
Здесь учтено равенство (3.19.17). Исключая из (3.19.19) угол β с помощью (3.19.12), получаем
˙ |
tg θ cos ϕ |
cos θ sin θ cos ϕ |
|
|||||
β = − |
|
|
|
ϕ˙ = − |
|
ϕ˙ . |
(3.19.20) |
|
|
|
|
|
|||||
|
1 + tg2 θ sin2 ϕ |
1 − sin2 θ cos2 ϕ |
|
|||||
Таким образом, угловая скорость крестовины полностью определена: |
||||||||
ω2 = ϕ˙ |
j − |
cos θ sin θ cos ϕ |
(sin ϕ i + cos ϕ k) . |
(3.19.21) |
||||
|
|
|||||||
1 − sin2 θ cos2 ϕ |
||||||||
Как видим, угловая скорость крестовины определяется относительно сложным выражением. Осталось вычислить угловую скорость выходного вала, которая определяется формулой (3.19.15). Из последней получаем
˙ |
cos θ |
|
||
ψ = |
1 − sin2 |
|
ϕ˙ . |
(3.19.22) |
|
θ cos2 ϕ |
|
||
156 |
Глава 3. Кинематика: спинорные движения |
Отсюда видим, что угловая скорость выходного вала переменна во времени при θ = 0, даже если угловая скорость входного вала постоянна. Обратим внимание на сложный характер зависимости угловой скорости выходного вала от углов θ и ϕ. Пусть, например, скорость входного вала постоянна и равна ϕ˙ = ω1. Тогда имеем ϕ = ω1t. Рассмотрим теперь моменты времени такие, что ω1t = πk. В эти моменты времени, согласно (3.19.22), имеем
˙ |
ϕ˙ |
(3.19.23) |
|
ψ = |
cos θ |
. |
|
При θ = π/2 угловая скорость выходного вала становится бесконечно большой. Из общих соображений, т.е. исходя из здравого смысла, этот результат кажется сомнительным. Сомнения увеличиваются еще больше, если мы обратимся непосредственно к формуле (3.19.22). Полагая в ней θ = π/2, получаем,
что ˙ = . Здесь мы встречаемся с любопытными особенностями. С чисто
ψ 0
математической точки зрения, мы имеем, хотя и не совсем стандартную, но хорошо известную ситуацию, когда предел функции двух переменных зависит от направления, по которому вычисляется этот предел. Иными словами, с математической точки зрения ничего особенно удивительного в полученном результате нет. Однако подобные фокусы с физической точки зрения вызывают протест у нашей интуиции. Обычно они указывают на не вполне удовлетворительную постановку задачи. Во всяком случае, в данной задаче это именно так. В самом деле, мы допустили, что входной вал может вращаться с заданной угловой скоростью независимо от угловой скорости выходного вала. Это допущение подразумевает, что входной вал вращается двигателем неограниченной мощности, каковых в действительности не существует. Чтобы яснее осознать необходимость двигателя неограниченной мощности, рассмотрим ситуацию, когда угол θ близок к π/2, т.е. θ = π/2 − ε, где 0 < ε << 1. Разлагая функции sin ε и cos ε в ряд по степеням ε и удерживая слагаемые до второго порядка малости включительно, выражение (3.19.22) переписываем в следующей форме
˙ |
2εϕ˙ |
2εω1 |
|
(3.19.24) |
|||
ψ = |
|
|
= |
|
|
. |
|
|
|
|
ω1t + ε2 cos2 ω1t |
||||
|
2 sin2 |
ϕ + ε2 cos2 ϕ 2 sin2 |
|
|
|||
|
|
|
|
|
˙ |
|
на интервале |
Читателю рекомендуется построить график функции ψ/ω1 |
|||||||
π/2 ≤ ω1t ≤ 3π/2 при ε = 0.001. Из графика видно, что при подходе к точке ω1t = π угловая скорость выходного вала начинает очень быстро нарастать до бесконечно большой величины. После прохождения этой точки угловая скорость выходного вала начинает столь же быстро уменьшатся. Вообразим теперь, что на выходной вал посажен массивный маховик. Тогда двигатель,
3.20. Сложное движение материальной точки |
157 |
подключенный к входному валу, должен почти мгновенно раскрутить этот маховик, а затем почти мгновенно затормозить его. Это было бы возможно только в том случае, если бы двигатель обладал бесконечной мощностью, что практически невозможно. Если мы хотим использовать двигатель ограниченной мощности, то чисто кинематических рассмотрений уже недостаточно. Необходимо привлекать законы механики. Кроме того, некоторые режимы работы требуют другого конструктивного исполнения вилки выходного вала, но на кинематических соотношениях это не отражается.
3.20. Сложное движение материальной точки
В приложениях часто используется так называемая лабораторная система отсчета, в которой производятся разного рода измерения. Вместе с тем, лабораторная система отсчета сама движется относительно основной системы отсчета. Последняя в механике и классической физике должна быть инерциальной, ибо в ней и только в ней вводятся такие понятия, как воздействия (силы, моменты и т.д.) и формулируются фундаментальные законы. Инерциальные системы отсчета будут введены во второй части курса. В кинематике мы должны просто научиться пересчитывать результаты лабораторных измерений в соответствующие результаты, имеющие смысл в основной системе отсчета. Чтобы яснее осознать все нижеследующее, рассмотрим воображаемую задачу о полете мухи (материальной точки) в салоне самолета, совершающего полет. Лабораторную систему отсчета естественно связать с самолетом, который, в свою очередь, будем рассматривать как абсолютно твердое тело.
Выберем какую-либо точку Q, которая фиксирована относительно самолета.
−−→ −→ −→
Выберем тройку материальных векторов QA, QB, QC таких, что при t = 0 (например, при посадке в самолет в аэропорту) они совпали бы с векторами
dm : dm · dn = δmn, |
(3.20.1) |
заданными в основной системе отсчета. При этом
−−→ |
|
d1, |
−→ |
|
d2, |
−→ |
|
d3. |
(3.20.2) |
QA |
|
QB |
|
QC |
|
|
Введем материальные координаты x1, x2, x3, жестко связанные с самолетом. Тогда положение точки самолета с координатами xm определяется радиусвектором
r = x1 d1 + x2 d2 + x3 d3 ≡ xm dm. |
(3.20.3) |
Пока самолет стоит на месте, лабораторная система отсчета совпадает с основной системой отсчета, связанной с Землей. Допустим, что по салону летает

158 Глава 3. Кинематика: спинорные движения
муха. Пассажир, сидящий в салоне, будет отмечать ее движение вектором
rf(t) = xfm(t) dm, |
(3.20.4) |
где xmf (t) координаты мухи в момент времени t.
В дальнейшем индекс f будем опускать и, вместо (3.20.4), писать
r(t) = xm(t) dm. |
(3.20.5) |
Надеемся, что читатель не спутает векторы (3.20.3) и (3.20.5). Однако начинающим лучше все-таки использовать более громоздкое, но более точное, обозначение (3.20.4). Пусть самолет приходит в движение и взлетает. Для
−−→ −→
пассажира ничего не изменится поскольку и материальные векторы QA, QB,
−→
QC (а, следовательно, и векторы dm), и материальные координаты xm для него
останутся неизменными. Движение мухи пассажир будет по-прежнему фиксировать (измерять) с помощью вектора (3.20.4) или, что то же самое, (3.20.5). Однако для наблюдателя, неподвижного относительно основной системы отсчета, ситуация радикально изменится. Лабораторная система отсчета для этого наблюдателя, в отличие от пассажира самолета, уже движется. В частности,
движутся точка |
Q |
|
|
|
|
|
|
|
|
QA |
QB |
QC |
. В то же время, |
||||
|
и материальные векторы −− , |
− |
, |
− |
|
||||||||||||
материальные координаты |
xm |
остаются |
неизменными как для пассажира, так |
||||||||||||||
|
|
|
→ |
→ |
|
→ |
QA QB QC |
||||||||||
и для неподвижного наблюдателя. Пусть материальные векторы −− , |
− |
, − |
|||||||||||||||
в момент времени |
t |
в основной (“неподвижной”) системе |
отсчета занимают |
||||||||||||||
|
|
→ |
→ |
→ |
|||||||||||||
положения векторов |
|
|
|
−→ |
|
|
|
−→ |
|
|
|
|
|
|
|||
|
−−→ |
|
D1 |
( ) |
D2 |
( ) |
D3( ) |
|
(3.20.6) |
||||||||
|
QA |
|
t , QB |
|
|
t , QC |
|
t . |
|
|
|||||||
Поэтому, с точки зрения неподвижного наблюдателя, положение мухи в основной системе отсчета задается вектором
R(t) = RQ(t) + xm(t) Dm(t). |
(3.20.7) |
Введем в рассмотрение тензор поворота
P(t) = Dm(t) dm, |
(3.20.8) |
где по индексу m подразумевается суммирование от 1 до 3. Из (3.20.8) имеем
Dm(t) = P(t) · dm. |
(3.20.9) |
Подставляя (3.20.9) в (3.20.7), получаем
R(t) = RQ(t) + xm(t) P(t) · dm = RQ(t) + P(t) · xm(t) dm.
3.20. Сложное движение материальной точки |
159 |
Вспоминая (3.20.5), окончательно получаем
R(t) = RQ + P(t) · r(t). |
(3.20.10) |
Сравнивая это выражение с основным уравнением кинематики абсолютно твердого тела, видим их большое сходство, что, впрочем, следовало ожидать. Роль абсолютно твердого тела в (3.20.10) выполняет лабораторная система отсчета. Роль полюса выполняет начало Q в лабораторной системе отсчета. Единственное различие состоит в том, что вектор r = rA − rQ, который в основном уравнении кинематики абсолютно твердого тела определял отсчетное положение рассматриваемой точки A, теперь определяет положение точки, движущейся относительно лабораторной системы отсчета. Аналогия будет видна еще лучше, если уравнение (3.20.10) переписать в виде
RA(t) = RQ + P(t) · (rA(t) − rQ), |
(3.20.11) |
где метка A соответствует мухе.
Вектор rA(t) определяет положение мухи с точки зрения наблюдателя, неподвижного относительно лабораторной системы отсчета, причем вектор rQ не зависит от времени. Вектор RA(t) определяет положение той же самой мухи с точки зрения наблюдателя, неподвижного в основной системе отсчета. Подчеркнем, что упоминания о наблюдателях не влекут за собой никаких формальных следствий. Они важны только для правильной интерпретации. Все векторы, входящие в (3.20.10) или (3.20.11), определены в основной (неподвижной) системе отсчета. В дальнейшем строчными буквами будем обозначать величины, наблюдаемые пассажиром в лабораторной системе отсчета. Прописными буквами будем обозначать величины, воспринимаемые наблюдателем в основной системе отсчета.
Для вычисления скорости мухи нужно продифференцировать (3.20.10) по времени. В результате получим
V(t) = VQ + ω(t) × P(t) · r(t) + P(t) · v, |
|
где |
|
˙ |
(3.20.12) |
P = ω × P, v = r˙. |
Исключая из предыдущего равенства вектор P · r с помощью (3.20.10),
получаем |
|
V(t) = VQ + ω × (R − RQ) + P · v. |
(3.20.13) |
Вучебниках по теоретической механике эту формулу обычно записывают
ввиде
V(t) = Ve + Vr, |
(3.20.14) |
160 |
Глава 3. Кинематика: спинорные движения |
|
где |
Ve = VQ + ω × (R − RQ), Vr = P · v. |
|
Вектор |
(3.20.15) |
|
Ve называется переносной скоростью, он характеризует скорость |
||
той точки лабораторной системы отсчета, в которой в данный момент времени находится муха. Вектор Vr называется вектором относительной скорости и является скоростью мухи относительно лабораторной системы отсчета с точки зрения наблюдателя в основной системе отсчета.
Обратимся к вычислению ускорений. Для этого достаточно продифференцировать (3.20.13) по времени. Тогда получим
W = WQ + ω × (R − RQ) + ω × (V − VQ) + ω × P · v + P · v˙. |
||
˙ |
|
|
Исключая отсюда вектор V − VQ с помощью равенства (3.20.13) и проводя |
||
перегруппировку слагаемых, получаем |
|
|
W = WQ + W · (R − RQ) + 2ω × P · v + P · w, |
(3.20.16) |
|
где |
˙ |
|
W |
(3.20.17) |
|
|
= ω × E + ω × E × ω, w = v˙. |
|
Тензор W называется тензором угловых ускорений лабораторной системы отсчета. Он совпадает с тензором угловых ускорений абсолютно твердого тела. Вектор w есть ускорение мухи относительно лабораторной системы отсчета с точки зрения пассажира самолета. Выражение (3.20.16) часто записывают в виде
W = We + Wc + Wr, |
(3.20.18) |
где |
|
We = WQ + W · (R − RQ), Wc = 2ω × P · v, Wr = P · w. |
(3.20.19) |
Вектор We называется переносным ускорением и выражает ускорение той точки лабораторной системы отсчета, в которой в данный момент времени находится муха. Вектор Wc называется ускорением Кориолиса´. Вектор Wr называется относительным ускорением. В приложениях удобнее работать непосредственно с формулой (3.20.16).
3.21. Сложные движения абсолютно твердого тела
В предыдущем параграфе были рассмотрены сложные движения материальной точки. При этом сложным называлось движение, которое было композицией двух движений: движения материальной точки относительно лабораторной системы отсчета и движения самой лабораторной системы отсчета
3.21. Сложные движения абсолютно твердого тела |
161 |
относительно основной, условно неподвижной, системы отсчета. Аналогичные построения нетрудно распространить на сложные движения абсолютно твердого тела.
Продолжим аналогию с полетом мухи (материальной точки) в салоне самолета. Только вместо мухи будем рассматривать шляпу, которой решили перебрасываться два чрезмерно любознательных пассажира, сидящих в разных концах салона, с целью исследования закономерностей ее полета. При этом их интересовали не только положения шляпы в полете, но и ее ориентация относительно салона самолета.
Лабораторную систему отсчета (ЛСО) жестко свяжем с салоном самолета.
Выберем точку Q, фиксированную относительно самолета и тройку матери-
−−→ −→ −→
альных векторов QA, QB, QC, которые в отсчетном положении соответствуют
векторам
−−→ |
|
d1 |
−→ |
|
d2 |
−→ |
|
d3 |
, |
dm · ds = |
δ |
ms |
. |
(3.21.1) |
QA |
|
, QB |
|
, QC |
|
|
|
|
Векторы dm определены в основной системе отсчета. Таким образом, лабораторная система отсчета порождается репером
{Q, d1, d2, d3}
и материальными координатами xm. Положение точки лабораторной системы отсчета с координатами xm определяется заданием вектора
x = xmdm. |
(3.21.2) |
Положение этой же точки лабораторной системы отсчета в основной системе отсчета в отсчетный момент времени определяется вектором
r = rQ + x = rQ + xmdm. |
(3.21.3) |
Вернемся к лабораторной системе отсчета. Основная теорема кинематики абсолютно твердого тела полностью сохраняется в лабораторной системе отсчета. Поэтому имеем
XA(t) = XS(t) + P(t) · (xA − xS), |
(3.21.4) |
где точка S есть произвольно выбираемая точка шляпы (полюс), точка A есть рассматриваемая точка шляпы, xA и xS суть векторы положения точек A и S в отсчетном положении в лабораторной системе отсчета, векторы XA XS суть векторы положения точек A и S в актуальном положении в лабораторной системе отсчета, P(t) есть тензор поворота шляпы в лабораторной системе отсчета.
