
Zhilin_Fundamental_Laws_Book
.pdf32 |
Глава 1. Законы равновесия тел |
|
||||
R(s) |
dR(s) |
|
|
|
|
|
t(s) = |
, |
|dR| = ds |
|t(s)| = 1. |
(1.6.1) |
||
|
||||||
ds |
||||||
Второе из уравнений (1.5.8) есть условие нерастяжимости нити. Нить будем считать однородной. Массу dm бесконечно малой части нити ds вычисляем по формуле dm = ρds, где ρ = const называется погонной плотностью массы (масса на единицу длины). В качестве тела A выберем часть нити, заключенную между точками s1 и s2 (рис. 1.8). На массу dm нити действует поле тяготения Земли, которое создает силу F(dm, E) = dm g. Таким образом, полная сила, действующая на тело A со стороны Земли, вычисляется по формуле
s2
F(A, E) = gρds.
s1
Силу, действующую на тело A, со стороны нити, находящейся правее точки s2, обозначим вектором T(t)(s2), где индекс (t) указывает, что вектор T(t)(s2) действует на площадку, ортогональную вектору единичной касательной t, т.е. на площадку поперечного сечения нити. Этот вектор моделирует воздействие части нити, находящейся со стороны положительного направления t. Так что индекс (t) несет смысловую нагрузку. Силу, действующую на тело A, со стороны нити, находящейся левее точки s1, обозначим вектором T(−t)(s1). Здесь индекс (−t) указывает, что вектор T(−t)(s1) моделирует воздействие части нити, находящейся со стороны положительного направления вектора (− t). Тогда первый закон статики можно записать в виде
F(A, Ae) = |
s |
|
2 |
gρds + T(−t)(s1) + T(t)(s2) = 0. |
(1.6.2) |
|
s |
|
|
|
|
|
|
1 |
|
|
|
Равенство (1.6.2) следует немного преобразовать. Заметим, что оно справедливо при любом выборе точек s1 и s2. Поэтому сделаем в (1.6.2) предельный переход при s1 → s + 0, s2 → s − 0. Тогда интеграл в (1.6.2) устремится к нулю и первый закон статики принимает вид
T(−t)(s) + T(t)(s) = 0 T(−t)(s) = − T(t)(s). |
(1.6.3) |
Это аналог третьего закона Ньютона о действии и противодействии. Введем обозначения
T(t)(s) ≡ T(t)(s), T(−t)(s) = −T(s).
В принятых обозначениях можем записать |
s1 |
ds ds. |
|
T(−t)(s1) + T(t)(s2) = T(s2) − T(s1) = |
|||
|
s2 |
dT(s) |
|
1.6. Равновесие нерастяжимой нити с закрепленными концами |
33 |
Теперь первый закон статики (1.6.2) принимает вид
s2 |
dT(s) |
|
|
s1 |
|
+ ρg ds = 0. |
(1.6.4) |
ds |
Упражнение: доказать, что интеграл (1.6.4) обращается в нуль при произвольном выборе пределов интегрирования тогда и только тогда, когда подынтегральное выражение обращается в нуль.
Таким образом, имеем локальную форму первого закона статики
dT(s) |
+ ρg = 0. |
(1.6.5) |
|
ds |
|||
|
|
Это и есть уравнение, полученное Я. Бернулли в 1691 г., в других, разумеется, обозначениях. С той поры миновало три столетия. Современная механика обрела совершенно другое лицо. Но уравнение (1.6.5) осталось и останется в будущем неизменным. То же самое можно сказать о многих других фундаментальных уравнениях механики. Способность рациональной механики получать уравнения, справедливые во все времена, является ее уникальным достоинством. Более того, уравнение (1.6.5) было выведено для тонкой гибкой нити. Но область его применимости много шире. Например, оно справедливо для тонкой струи воды, для резинового растяжимого шнура, для тонкого стержня, сопротивляющегося изгибу, и т.д. При выводе (1.6.5) использовался только первый закон статики, который имеет неограниченную область применимости.
В отличие от рассмотренных ранее задач, при равновесии деформируемых тел силы подчиняются не алгебраическим, а дифференциальным уравнениям. Поэтому здесь уже не подходит рассуждение, основанное на подсчете числа неизвестных и числа уравнений. Если число независимых уравнений совпадает с числом входящих в них неизвестных, то последние, как правило, могут быть найдены. В данном случае мы имеем одно векторное уравнение (1.6.5) для одного неизвестного вектора T(s). Тем не менее, определить этот вектор мы не можем. Действительно, интегрируя уравнение (1.6.5), получаем
T(s) = T0 − ρg s, T0 ≡ T(0). |
(1.6.6) |
Отсюда видим, что вектор натяжения в нити определился с точностью до произвольного постоянного вектора T0. Чтобы определить этот вектор, необходимо знать так называемые краевые условия, т.е. значение вектора T(s) при s = 0 или s = l. В данном случае мы не знаем ни того, ни другого. Поэтому первого закона статики нам не достаточно, чтобы полностью решить задачу. Как же тогда Я. Бернулли сумел решить задачу? Ведь второй закон статики

34 |
Глава 1. Законы равновесия тел |
ему не был известен. Здесь мы сталкиваемся с ситуацией, когда выдающиеся личности могут обходиться без законов, довольствуясь своей интуицией и здравым смыслом. Так и Я. Бернулли использовал факт, который ниже будет доказан на основе второго закона статики. Аналогична ситуация с третьим законом Ньютона. В настоящее время это доказанная теорема, а отнюдь не аксиома, как это было у Ньютона. Подробнее об этом будет сказано в другом месте.
Итак, обратимся ко второму закону статики. Окружение тела A состоит из трех тел: Земли, т.е. тела E, нити правее точки s2 и нити левее точки s1. Само тело является объединением бесконечно малых частей с массой dm = ρds. Вычислим момент, действующий на эту малую часть нити
MO(dm, E) = R(s) × gdm = R(s) × gρds.
Собственно момент здесь равен нулю, поскольку поворот частицы с массой dm вокруг самой себя в поле тяготения не вызывает сопротивления. Полный момент, действующий на тело A со стороны Земли, вычисляется как сумма
s2
MO(A, E) = R(s) × gρds. (1.6.7)
s1
Вычислим момент, действующий на тело A со стороны нити, находящейся правее точки s2. Он равен
R(s2) × T(t)(s2) ≡ R(s2) × T(s2).
Здесь собственно момент также равен нулю, поскольку нить, находящаяся правее точки s2, не сопротивляется повороту тела A вокруг точки s2. Подчеркнем, что это очевидное с интуитивной точки зрения обстоятельство нельзя доказать формальными методами. Аналогичное выражение мы имеем для момента, действующего на тело A со стороны нити, находящейся левее точки
s1
R(s1) × T(−t)(s1) = −R(s1) × T(s1).
Суммируя последние два момента, получаем
R(s1) × T(−t)(s1) + R(s2) × T(t)(s2) = R(s2) × T(s2) − R(s1) × T(s1) =
s2 d
= s1 ds [R(s) × T(s)] ds (1.6.8)
Суммируя моменты (1.6.7) и (1.6.8), записываем второй закон статики в
следующем виде |
R(s) × |
|
+ ρ g + |
ds × T(s) ds = 0. (1.6.9) |
|
MO(A, Ae) = |
s1 |
ds |
|||
|
s2 |
|
dT(s) |
|
dR(s) |
1.6. Равновесие нерастяжимой нити с закрепленными концами |
35 |
Учитывая первый закон статики (1.6.5) и произвольность выбора пределов интегрирования в (1.6.9), получаем локальную форму второго закона статики
dR(s) |
× T(s) = 0 |
T(s) = λ(s) |
dR(s) |
, |
(1.6.10) |
ds |
ds |
где величина λ(s) есть произвольная скалярная функция.
Иными словами, вектор усилия в нити должен быть направлен по касательной к нити. Так требует второй закон статики и именно это принял Я. Бернулли из интуитивных представлений. Тем самым, он выполнил второй закон статики, не подозревая его существования. При λ(s) > 0 сила в нити является растягивающей. При λ(s) < 0 сила в нити является сжимающей. Понятно, что нить не сопротивляется сжатию и может работать только на растяжение, т.е. нас интересуют только положительные значения λ(s). Тем не менее, это условие заранее не принимается и будет установлено в ходе решения задачи. Подставляя (1.6.10) в (1.6.6), получаем следующее дифференциальное уравнение
λ(s) |
dR(s) |
= T0 − ρgs; R(0) = 0, R(l) = a i. |
(1.6.11) |
|
ds |
||||
|
|
|
Последние два условия называются краевыми условиями. Они фиксируют тот факт, что концы нити закреплены, т.е. их положения заданы. Прежде, чем приступить к решению уравнения (1.6.11), его удобно немного преобразовать и привести к безразмерному виду. В координатном виде уравнение (1.6.11)
записывается в виде |
|
|
|
|
|
|
λ(s) |
dX(s) |
= P, λ(s) |
dY(s) |
= Q + ρ g s; |
|
|
ds |
ds |
|
||||
|
|
|
|
|
||
R = Xi + Yj, |
T0 = Pi + Qj, g = −gj. |
(1.6.12) |
||||
Для упрощения дальнейших выкладок воспользуемся очевидным условием симметрии (рис. 1.8). Видим, что функция Y, т.е. вертикальная составляющая вектора R, достигает своего минимума при s = l/2. Поэтому производная от функции Y по переменной s должна обращаться в нуль при s = l/2. Записывая второе из уравнений (1.6.12) в точке s = l/2, находим постоянную Q = −ρ g l/2. Можно было бы не использовать соображения симметрии, ре-
зультат получился бы тем же самым. Введем новые переменные |
|
|||||||||||||||||||||||
|
X = |
l |
x, |
Y = |
l |
y, |
λ = |
ρgl |
μ, |
|
ξ = |
2s |
− 1, |
P = |
ρgl |
p. |
(1.6.13) |
|||||||
|
|
|
|
|
|
|||||||||||||||||||
2 |
|
2 |
|
2 |
|
|
|
|
|
l |
2 |
|
|
|||||||||||
В новых переменных система (1.6.12) принимает вид |
|
|||||||||||||||||||||||
|
dx |
|
dy |
|
dx |
2 |
|
|
dy |
2 |
|
|
|
|
|
|||||||||
μ |
|
= p, |
μ |
|
= ξ, |
|
|
|
+ |
|
|
|
= 1; |
−1 < ξ < 1. |
(1.6.14) |
|||||||||
dξ |
dξ |
dξ |
dξ |
|||||||||||||||||||||

36 Глава 1. Законы равновесия тел
Третье уравнение в системе (1.6.14) есть условие нерастяжимости нити (1.6.1). Возведем в квадраты первое и второе уравнения в системе (1.6.14) и сложим результаты. При этом учтем третье уравнение в системе (1.6.14). Тогда
получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
μ2 = p2 + ξ2 |
|
|
|
μ = ε |
p2 + ξ2, |
ε = ±1. |
(1.6.15) |
||||||||||||||||
Теперь система (1.6.14) |
переписывается в виде |
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
dx |
= |
|
|
p |
|
|
, |
|
|
dy |
= |
|
|
|
ξ |
|
|
, |
−1 < ξ < 1. |
(1.6.16) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
dξ |
|
ε p2 + ξ2 |
|
|
dξ |
ε p2 + ξ2 |
|
|
|
|
|
|
|
|||||||||||||
К системе |
(1.6.16) необходимо добавить краевые условия |
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
x(−1) = 0, |
|
x(1) = 2a/l, y(−1) = 0, |
|
y(1) = 0 |
|
(1.6.17) |
||||||||||||||||||||
Интегрируя уравнения (1.6.16), получаем |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
p |
|
p2 + ξ2 + ξ |
|
|
|
|
|
|
p2 |
ξ2 |
+ |
d |
|
||||||||
|
|
|
x(ξ) = |
|
ln |
|
|
|
|
|
|
|
, y(ξ) = |
|
+ε |
. |
|
||||||||||
|
|
|
ε |
|
|
c |
|
|
|
|
|
||||||||||||||||
В это решение вошли три неизвестные постоянные p, c, d. Кроме того, это решение содержит неопределенную величину ε. Для их определения и служат краевые условия. Постоянные c, d определяются по первому и третьему условиям в (1.6.17). При этом четвертое условие выполнено тождественно, что является следствием использованного ранее условия симметрии. После
определения постоянных c и d решение принимает вид |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
p |
|
|
p2 + ξ2 + ξ |
|
|
|
|
p2 |
+ 1 − p2 |
+ ξ2 |
||||||||||||||
x(ξ) = |
|
ln |
|
|
|
|
− 1 |
, y(ξ) = − |
|
|
ε |
. |
|||||||||||||
ε |
|||||||||||||||||||||||||
p2 + 1 |
|||||||||||||||||||||||||
Для нахождения |
постоянных p, ε осталось выполнить второе краевое усло- |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
вие в (1.6.17). Оно сводится к выполнению равенства |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
2a |
|
p |
p2 + 1 + 1 |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
= |
|
ln |
|
− 1. |
|
|
|
(1.6.18) |
||||||||
|
|
|
|
|
|
|
l |
ε |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
p2 + 1 |
|
|
|
|||||||||||||||
Получили трансцендентное |
уравнение для нахождения вещественной по- |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
стоянной p, которое содержит параметр ε. Из уравнения (1.6.18) видим, что отношение p/ε всегда положительно. Поэтому p/ε = |p/ε| = |p|. При ε = −1 постоянная p и сила натяжения в нити λ отрицательны, как это видно из уравнений (1.6.13) и (1.6.15). При ε = 1 постоянная p и сила натяжения в нити λ положительны в соответствии с уравнениями (1.6.13) и (1.6.15). При обоих значениях параметра ε уравнение (1.6.18) можно переписать в виде
|
√ |
|
|
|
|
|
|
|
2 |
+ 1 + z |
|
|
|
2 |
|||
|
|
|
||||||
νz = ln |
√ |
z |
exp(νz) = |
z2 + 1 + z ≡ f(z), (1.6.19) |
||||
|
|
|
||||||
z2 |
+ 1 − z |
|||||||
1.6. Равновесие нерастяжимой нити с закрепленными концами |
37 |
|||||
где |
|
|
|
|
|
|
ν = |
2a |
, |
z = |
1 |
. |
|
|
|
|
||||
l |
|p| |
|
||||
Уравнение (1.6.19) можно преобразовать к более простому виду. Для этого сначала нужно сделать замену переменной z → −z, а затем сложить получившееся уравнение с уравнением (1.6.19). В результате получим уравнение
ch νz = 1 + 2z2.
Это уравнение удобно для при- |
|
|
|
|
|
ν = 1.8 |
|
|
||
|
|
|
|
|
|
|
||||
ближенного аналитического опреде- |
|
|
|
|
|
|
|
|||
0.4 |
|
|
|
|
|
|
|
|||
ления неизвестной z, но мы бу- |
0.2 |
|
|
|
|
|
|
|
||
дем обсуждать уравнение (1.6.19). |
|
|
|
|
|
|
|
|
|
|
И левая, и правая части уравнения |
|
0.2 |
0.4 |
0.6 |
0.8 |
1 |
1.2 |
|
||
-0.2 |
|
|
|
|
|
|
|
|
||
(1.6.19) равны единице при z = 0, |
|
|
|
|
|
|
ν = 1.7 |
|||
-0.4 |
|
|
|
|
|
|
||||
что соответствует бесконечно боль- |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||
шой величине усилия в нити. Это |
Рис. 1.9. Вычисление корней |
|||||||||
физически не реализуемая ситуация, |
||||||||||
|
|
|
|
|
|
|
|
|
||
поскольку любая нить обладает конечной прочностью на разрыв. При больших z левая часть (1.6.19) больше, чем правая, поскольку экспонента растет быстрее любой степенной функции. Следовательно, уравнение (1.6.19) имеет решение, отличное от нулевого, только тогда, когда при малых z правая часть (1.6.19) растет быстрее, чем левая часть. О скорости роста этих функций при малых z можно судить по производной от этих функций в нуле. Значение производной от экспоненты в нуле равно ν. Значение производной от функции f(z) в нуле равно 2. Поэтому уравнение (1.6.19) имеет решение только при выполнении условия ν < 2 a < l. К сожалению, корень уравнения (1.6.19)
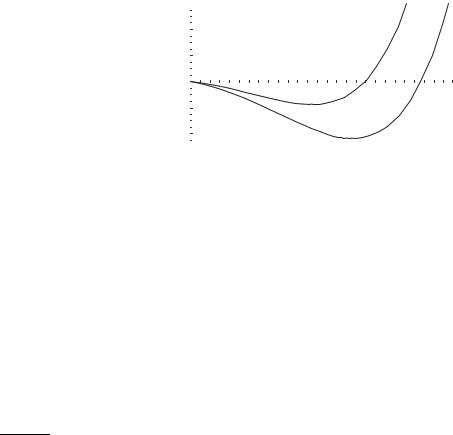
можно найти только численными методами. На рис. 1.9 представлен график
√
функции exp νz − ( z2 + 1 + z)2 при различных значениях ν. Видим, что с увеличением ν величина z убывает, т.е. сила натяжения в нити растет.
Таким образом, в данной задаче имеется два решения. Одно решение соответствует значению параметра ε = 1 и описывает устойчивую равновесную конфигурацию нити. При этом стрела провисания нити, т.е. функция y(ξ), направлена вниз, как это видно из выражения для y(ξ). Второе решение соответствует значению параметра ε = −1 и описывает неустойчивую равновесную конфигурацию нити. При этом стрела прогиба нити направлена вверх. Для нити такая равновесная конфигурация нереализуема, но она возможна для арок, которые способны сопротивляться сжатию.
38 |
Глава 1. Законы равновесия тел |
1.7.Балка с защемленными концами
Впредыдущих пунктах рассматривались задачи, решение которых можно было построить используя только законы равновесия тел. Задачи подобного рода называются статически определимыми. Они часто встречаются на практике. Тем не менее, подавляющее большинство задач статики для своего решения требуют привлечения дополнительных законов, которые выражают наши интуитивные представления или экспериментальные закономерности. Эти дополнительные законы называются определяющими уравнениями и связывают воздействия с движениями, т.е. связывают силовые и кинематические характеристики. Следует отметить, что определяющие уравнения необходимы и при решении статически определимых задач, если желательно знать как изменяется конфигурация рассматриваемого тела в результате приложения к нему внешних воздействий. Простейшим и хорошо знакомым примером определяющего уравнения в механике является закон всемирного тяготения.
Определяющие уравнения будут об- |
|
s1 |
суждаться после введения фундамен- |
O |
B |
тальных законов механики. Здесь же |
|
s2 |
|
q(s) |
|
необходимо отметить, что определяю- |
|
|
|
|
|
щие уравнения не носят строго обяза- |
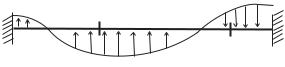
Рис. 1.10. Поперечный изгиб балки |
|
тельного и фундаментального харак- |
|
|
тера. Их можно, если в этом есть необходимость, изменять и уточнять. Но эти изменения и уточнения не должны противоречить фундаментальным законам, которые накладывают некоторые ограничения на конкретный вид определяющих уравнений. Представленную ниже задачу можно рассматривать как первое знакомство с определяющими уравнениями.
Рассмотрим задачу об изгибе однородной балки с защемленными концами (рис. 1.10). Эта задача сыграла выдающуюся роль в становлении рациональной механики. Краткая историческая справка будет приведена в конце этого параграфа. Пусть изначально прямолинейная балка с прямоугольным поперечным сечением защемлена своими концами в абсолютно твердые стены. Следуя историческим традициям, при написании всех уравнений балку будем рассматривать как линию, проходящую через центры поперечных сечений. Эту линию принято называть упругой линией. Тот факт, что балка отлична от линии, мы вспомним позднее при формулировке определяющих уравнений. Положение каждой точки этой балки будем определять заданием вектора
r(s) = s i, 0 ≤ s ≤ l, |
(1.7.1) |
где s — расстояние от левого конца балки до рассматриваемой точки, отсчитываемое вдоль упругой линии.
1.7. Балка с защемленными концами |
39 |
Упругую линию наделим массой, при этом массу бесконечно малой части линии ds будем определять по формуле dm = ρds, где ρ = const есть масса на единицу длины упругой линии. Выясним, что нам дадут законы статики, если мы всю балку целиком будем рассматривать как тело A. Левую стенку будем рассматривать как тело O, а правую стенку будем считать телом B. Пусть на единицу массы балки действует внешняя нагрузка q(s), создаваемая телом Q, так что сила F(dm, Q) вычисляется по формуле F(dm, Q) = q(s)ρds. Полная сила, создаваемая телом Q, вычисляется по формуле
F(A, Q) = |
0 qρds. |
|
|
l |
|
Запишем первый закон статики |
|
0 qρds = 0. |
F(A, Ae) = F(A, O) + F(A, B) + F(A, Q) = F(A, O) + F(A, B) + |
||
|
|
l |
(1.7.2) Уравнение (1.7.2) содержит два неизвестных вектора, выражающих реакции стенок. Их нельзя определить из одного уравнения. Поэтому необходимо для них выписать дополнительные уравнения. В предыдущих параграфах вопрос решался формулировкой второго закона статики, к которому мы сейчас
и обратимся. Имеем
MO(A, Ae) = MO(A, O) + MO(A, B) + MO(A, Q) = 0.
Здесь опорная точка и начало в системе отсчета выбраны на левом конце упругой линии. При вычислении момента MO(A, O) точку приведения принимаем совпадающей с опорной точкой. При этом собственно момент оказывается отличным от нуля, поскольку стенка препятствует повороту балки. При вычислении момента MO(A, B) точку приведения принимаем на правом конце балки. При этом собственно момент также оказывается отличным от нуля, поскольку и правая стенка препятствует повороту балки. При вычислении момента MO(A, Q) воспользуемся аксиомой аддитивности и запишем
MO(A, Q) = |
0 MO(A, qρds) = |
0 |
[r(s) × q(s)] ρds. |
|
l |
l |
|
Бесконечно малая часть dQ тела Q, создающая силу q(s)ρds, не препятствует повороту балки вокруг точки r(s). Поэтому собственно момент под знаком интеграла в вышеприведенном уравнении отсутствует.
Таким образом, второй закон статики принимает вид
l
LO(A, O) + li × F(A, B) + LB(A, B) + [r(s) × q(s)] ρds = 0. (1.7.3)
0
40 |
Глава 1. Законы равновесия тел |
Получили еще одно векторное уравнение, но оно не упрощает ситуацию, поскольку в него вошли еще два неизвестных вектора LO(A, O) и LB(A, B), моделирующие моментные реакции стенок. Итак получили систему двух векторных уравнений, в которые вошли четыре неизвестных вектора. Такие системы называются недоопределенными и имеют бесконечное множество решений. Поэтому такого рода задачи называются статически неопределимыми. Природу статической неопределенности можно понять из следующих рассуждений. Представим себе, что вырезы в стенках выполнены с небольшими начальными погрешностями. Например, они сделаны на разной высоте. Вставив балку в один из вырезов, мы полностью задаем положение балки, рассматриваемой как абсолютно твердое тело, в пространстве. Чтобы балку вставить во второй вырез, ее придется слегка изогнуть. Деформации балки существенно влияют на усилия и моменты, возникающие в балке. Это означает, что форма изгиба балки оказывается важной. Но законы статики никак не связаны с какими-либо кинематическими характеристиками, поэтому силовые и моментные характеристики в балке не могут определяться только законами статики. Для сравнения рассмотрим задачу, представленную на рис. 1.4. Если опоры будут выполнены неточно, то балку все равно можно положить на опоры без того, чтобы ее деформировать. Задача оказывается статически определимой.
Итак, в статически неопределимых системах необходимо принимать во внимание деформации тел. В таких случаях от интегральных уравнений равновесия типа (1.7.2) и (1.7.3) необходимо переходить к локальным формулировкам. Упругую линию деформированной балки будем определять заданием вектора R(s), связанного с вектором r(s) соотношением
R(s) = r(s) + U(s), |
(1.7.4) |
где вектор U(s) называется вектором перемещений, который переводит точку упругой линии с координатой s из начального (известного) положения r(s) в актуальное и заранее неизвестное положение R(s).
Вектор единичной касательной к деформированной упругой линии опреде-
ляется равенством |
|
|
|
|
|
|
t(s) = |
dR(s) |
dR(s) |
|
−1 |
(1.7.5) |
|
ds |
ds |
. |
||||
|
|
|
|
|
|
линейную теорию, в ко- |
Далее мы будем рассматривать так называемую |
||||||
|
|
|
|
|
|
|
торой перемещения будут считаться бесконечно малыми. Поэтому они будут сохраняться только тогда, когда они будут главными членами в тех или иных выражениях. Предположение о малости перемещений, во-первых, хорошо выполняется для твердых тел и, во-вторых, совершенно не меняет существа проблемы. Для малых перемещений выражение (1.7.5) можно существенно
|
|
|
1.7. Балка с защемленными концами |
|
|
41 |
||||||
упростить |
|
|
|
|
|
|
|
|
|
|
|
|
|
dR(s) |
|
dR(s) |
|
−1 |
|
dU(s) |
|
dU(s) |
|
−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t(s) = |
ds |
|
ds |
|
= i + |
ds |
i + |
ds |
|
= i. |
(1.7.6) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вывод локальной формы первого закона статики дословно повторяет вывод, проведенный в предыдущем параграфе для нити. В качестве тела A выбираем часть упругой линии, заключенной между произвольно выбираемыми точками s1 и s2, причем s1 < s2. Тогда имеем
F(A, Ae) = |
s1 |
q(s)ρds + T(−t)(s1) + T(t)(s2) = |
s1 |
|
ds |
+ ρq(s) ds = 0. |
|
s2 |
|
s2 |
|
dT(s) |
|
Повторяя рассуждения предыдущего параграфа, получаем локальную форму первого закона
dT(s) |
+ ρq(s) = 0, |
(1.7.7) |
|
ds |
|||
|
|
которое в точности повторяет уравнение (1.6.5), причем вектор усилий T(s) в балке имеет тот же смысл, что и в нити. Правда, он уже не будет направлен по касательной к деформированной упругой линии. Но на данном этапе рассуждений это ограничение не вводилось и для нити. Обратим внимание, что при выводе уравнения (1.7.7) предположение о малости перемещений не использовалось, т.е. оно верно и при больших перемещениях. Обратимся к выводу локальной формы второго закона статики. Здесь уже отличие от нити будет существенным. Преодолеть возникшую при этом проблему Я. Бернулли не сумел — см. конец этого параграфа. Момент, действующий на выделенную часть балки, т.е. на тело A, вычисляется стандартным образом, причем второй закон статики записывается в виде
MO(A, Ae) = R(s2) × T(s2) + M(t)(s2) − R(s1) × T(s1) + M(−t)(s1)+
s2
+ R(s) × q(s)ρds = 0, (1.7.8)
s1
где вектор M(t)(s2) моделирует собственно момент, действующий на тело A со стороны части балки, находящейся правее точки s2.
Вектор M(−t)(s1) моделирует собственно момент, действующий на тело A со стороны части балки, находящейся левее точки s1. Именно наличие этих моментов отличает балку от нити и выражает собой тот факт, что балка, в отличие от нити, сопротивляется изгибу, т.е. поворотам поперечных сечений
балки друг относительно друга. Переходя в равенстве (1.7.8) к пределу s |
1 |
→ |
|||||
s − 0, s2 |
→ |
s + 0, получаем |
|
|
|
||
|
M(−t)(s) = − M(t)(s) |
≡ |
− M(s). |
(1.7.9) |
|||
|
|
|
|
|
|
|
|
