Zhilin_Fundamental_Laws_Book

3.12. Определение поворота по угловой скорости

Допустим, что нам известен левый (правый) вектор угловой скорости. Кроме того, нам известно, что в момент сравнения t = τ тензор поворота равен единичному тензору

Требуется найти тензор поворота, отвечающий вектору угловой скорости ω(t). Запишем уравнение Пуассона

где ω(t) считается заданным.

Тензорное уравнение (3.12.2) эквивалентно девяти скалярным уравнениям первого порядка для координат тензора P(t) = Pmn(t)em en. Однако не все эти уравнения являются независимыми. В (3.12.2) только три уравнения оказываются независимыми. Поэтому система (3.12.2) является системой обыкновенных дифференциальных уравнений третьего порядка. Несмотря на то, что сказанное отнюдь не самоочевидно для начинающего, мы не будем заниматься доказательствами немедленно, а изложим их немного позднее, когда ознакомимся с различными представлениями тензора поворота. В теории обыкновенных дифференциальных уравнений задача их интегрирования при определенных начальных условиях типа (3.12.1) называется задачей Коши. Таким образом, нахождение тензора поворота по заданной угловой скорости ω(t) сводится к интегрированию уравнения (3.12.2) при начальных условиях (3.12.1). Эта задача Коши весьма специфична и исследована еще в прошлом веке Жаном Дарбу (1842-1917). Поэтому задачу интегрирования уравнения (3.12.2) при начальных условиях (3.12.1) в динамике твердого тела принято называть задачей Дарбу.

Теорема: решение задачи Дарбу, т.е. решение уравнения (3.12.2) при начальных условиях (3.12.1), существует, единственно и является тензором поворота.

Доказательство. Существование и единственность решения задачи Коши, частным случаем которой является задача Дарбу, доказывается в теории обыкновенных дифференциальных уравнений. Поэтому нам необходимо доказать только последнее утверждение теоремы, т.е. доказать, что тензор P(t), являющийся решением уравнения (3.12.2) и удовлетворяющий условию (3.12.1), является тензором поворота. Пусть P(t) удовлетворяет уравнению (3.12.2) и начальному условию (3.12.1). Составим тензор B(t)

Здесь мы учли, что P(τ) = E в силу (3.12.1). Продифференцируем (3.12.3) по времени и воспользуемся уравнением (3.12.2) для того, чтобы исключить производные от P(t) по времени. Получим

= ω × B − P · PT × ω = ω × B − B × ω.

Таким образом, если тензор P(t) удовлетворяет уравнению (3.12.2), то

Кроме того, B(t) при t = τ должен удовлетворять условию (3.12.3): B(τ) = E. Иными словами, для тензора B(t) мы также получили задачу Коши, решение которой существует и единственно. На первый взгляд, решение задачи (3.12.4) и (3.12.3) ничуть не проще, чем решение задачи Дарбу (3.12.2) и (3.12.1). Но все дело в том, что решение задачи (3.12.4) и (3.12.3) легко угадать. Именно угадать, а не построить на основе каких-либо общих методов. Действительно, легко видеть, что тензор B(t) = E удовлетворяет как уравнению (3.12.4), так и начальному условию (3.12.3). Поскольку решение задачи Коши (3.12.4) и (3.12.3) единственно, то тензор B(t) = E является единственным решением задачи. Таким образом, получается, что тензор P(t) при всех t удовлетворяет условию

B(t) = P(t) · PT (t) = E,

из которого следует, что тензор P(t) — ортогонален. Как следствие получаем

Поскольку при t = τ имеем det P(τ) = det E = 1, то det P(t) = 1 при всех t. Итак, решение задачи Дарбу является тензором поворота.

Вкачестве момента сравнения τ всегда можно выбрать значение τ = 0, т.е.

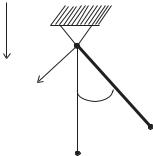
τпринять за начало отсчета времени. Но это не всегда удобно. Рассмотрим пример (рис. 3.7).

Пусть стержень OA подвешен с помощью шарнира в точке O и может совершать движения вокруг O в плоскости чертежа. Пусть на стержень действует поле силы тяжести g. Тогда если стержень слегка отклонить от вертикали и затем опустить, то он начнет совершать малые колебания около вертикали. Начальное положение стержня (на рисунке — это ОА) при t = 0 отклонено от вертикали. В качестве отсчетного положения удобно принять не это начальное

g

O

- m è

A

A’

Рис. 3.7. Выбор отсчетного положения

положение, а вертикальное положение стержня. Поэтому принимаем, что при каком-то τ < 0 стержень занимал вертикальное положение и тензор поворота P(τ) = E. При t = 0 тензор поворота имеет вид

P(0) = (1 − cos θ0) m m + cos θ0 E + sin θ0 m × E ≡ P0,

где m — ортогонален плоскости чертежа и направлен “от нас”. Задача Дарбу в этом случае принимает вид

Отметим одно свойство задачи Дарбу. На первый взгляд может показаться, что задача (3.12.5) линейна. Следовательно, ее общее решение должно быть суммой трех частных решений уравнения (3.12.5). Именно так гласит известная теорема из теории линейных дифференциальных уравнений третьего порядка. Здесь имеется одна тонкость, которая резко меняет ситуацию. Дело, конечно, в начальном условии. Тензор P0 в (3.12.5) должен быть тензором поворота. Повороты, как мы уже знаем, мультипликативны, а вовсе не аддитивны. Поэтому сумма частных решений нас попросту не устраивает. Как же строить в таком случае общее решение задачи Дарбу (3.12.5)? Оказывается, что достаточно найти одно частное решение уравнения (3.12.5), но такое, что оно является тензором поворота. Последнее обстоятельство существенно затрудняет построение решения задачи Дарбу. В частности, оно делает проблематичным численное построение решения, ибо строить численно матрицы, строго удовлетворяющие условиям ортогональности, весьма затруднительно, если вообще возможно. Позднее мы покажем, как устранить описанное затруднение. Сейчас мы ограничимся демонстрацией того, что одного частного решения уравнения (3.12.5), без учета начального условия, достаточно, чтобы найти общее решение задачи (3.12.5). Пусть тензор поворота Q(t) является

каким-либо решением уравнения (3.12.5) без учета начального условия

является решением задачи (3.12.5).

Упражнение. Доказать последнее утверждение.

3.13. Вращение вокруг фиксированной оси

Повороты и вращения твердого тела вокруг фиксированной оси часто встречаются в приложениях, например, при плоских движениях тела. Этот случай наиболее прост для интуитивного восприятия спинорного движения. Не случайно поэтому в элементарных учебниках по физике угловая скорость вводится именно на примере вращения тела вокруг фиксированной оси. Рассмотрим диск, который поворачивается (вращается) вокруг собственной оси, причем плоскость диска сохраняет неизменное положение. За время Δt диск поворачивается на угол Δθ(t). Ось диска совпадает с прямой, натянутой на единичный

В некоторых книгах определение (3.13.1) распространяется на общий случай, когда m меняется во времени. Интуитивно не вполне ясно, всегда ли приемлемо определение угловой скорости в виде (3.13.1). Однако совершенно ясно, что любое приемлемое определение угловой скорости обязательно должно совпадать с (3.13.1) в описанной выше ситуации, т.е. когда вращение происходит вокруг фиксированной во времени оси. Проверим этот факт для левой и правой угловых скоростей, определенных посредством (3.11.5) и (3.11.8). Тензор поворота вокруг оси m дается теоремой Эйлера (3.3.1), причем

Это равенство, разумеется, справедливо всегда, а не только при m = const. Запишем теперь уравнение Пуассона

Умножим это равенство скалярно на вектор m справа и учтем, что

Иными словами, если повороты происходят вокруг фиксированной оси, то и вращения происходят вокруг этой же фиксированной оси. Оси поворота и вращения совпадают. Подставляя (3.13.4) в (3.13.3), получаем

Вычислим теперь след от обеих частей уравнения (3.13.5) и учтем равенства

Подставляя это соотношение в (3.13.4), получаем определение (3.13.1). Итак, левая угловая скорость при поворотах вокруг фиксированной оси совпадает с определением (3.13.1). Для правой угловой скорости имеем

т.е. правая и левая угловые скорости в этом случае совпадают. Ранее равенствами (3.10.2),(3.10.3) и (3.10.4) были введены три различных определения угловой скорости. При поворотах вокруг фиксированной оси все три определения приводят к одному и тому же вектору

Можно только пожалеть, что справедливость соотношений (3.13.7) исчерпывается случаем поворотов вокруг фиксированной оси. Весьма близким к рассмотренному случаю поворота вокруг фиксированной оси является случай вращения вокруг фиксированной оси

Для того, чтобы найти ось поворота, необходимо по ω(t) построить тензор поворота и найти его неподвижный вектор. Иными словами, необходимо решить задачу Дарбу

Введем следующие подстановки

Подставляя эти соотношения в (3.13.9) получаем следующую задачу для нового тензора поворота Q(t)

Докажем утверждение: производная от тензорной экспоненты exp[ϕ(t) A], где A = const, равна

Для доказательства (3.13.12) рассмотрим тензорный ряд, являющийся определением тензорной экспоненты

∞

exp(ϕ A) = m1!ϕm Am.

m=0

Дифференцируя этот ряд по времени и учитывая, что A — постоянный тензор, получаем

= ϕ˙ A · exp(ϕA) = ϕ˙ exp(ϕA) · A.

Здесь мы перешли к другому индексу суммирования k = m − 1. Обратим внимание, что условие A = const является весьма существенным. В противном случае, при дифференцировании тензорного ряда пришлось бы дифференцировать тензор A и ничего похожего на (3.13.12) не получилось бы. Проблема

в том, что тензоры и ˙ не коммутируют

A A

(t) · ˙ (t) = ˙ (t) · (t).

A A A A

Обратимся к решению задачи (3.13.11). Тензор поворота Q(t) ищем в виде

128 Глава 3. Кинематика: спинорные движения

Подставляя это выражение в (3.13.11), приходим к скалярному уравнению

Ось этого поворота совпадает с осью вращения n. Исходный тензор поворота P(t) согласно (3.13.10) имеет вид

где ϕ0 есть вектор начального поворота.

Вектор поворота, отвечающий тензору P(t), можно найти по формуле сложения векторов поворота (3.8.16). В результате получим, что неподвижный вектор тензора P(t) совпадает с осью вращения n тогда и только тогда, когда

вектор начального поворота ϕ0 лежит на оси вращения n.

Упражнение. Доказать это утверждение.

Если

θ × ϕ0 = 0,

то вектор поворота, отвечающий тензору поворота P(t), будет иметь переменное во времени направление.

3.14. Связь угловой скорости с вектором поворота

Угловая скорость вводится в рассмотрение с помощью уравнения Пуассона

Если тензор поворота задан, то угловая скорость определяется равенством

Для тензора поворота мы имеем несколько представлений. Одно из них выражалось формулой (3.3.1)

P = (1 − cos θ)m m + cos θ E + sin ϕ m × E, −π < θ < π, (3.14.3)

где угол поворота θ(t) и неподвижный вектор m(t) зависят от времени.

Упражнение. Доказать равенство

Для доказательства этого равенства достаточно продифференцировать (3.14.3) по времени, а результат подставить в (3.14.2). Начинающим весьма полезно проделать вывод (3.14.4).

Равенство (3.14.4) было строго получено в [17, 21]. Однако, в несколько другой трактовке, это равенство было известно еще Эйлеру [26]. Если вращение происходит вокруг фиксированной оси m˙ = 0, то из (3.14.4) получаем (3.13.7). Если в качестве отсчетного положения выбрать положение в данный момент времени, то получим определение угловой скорости, принятое в некоторых

Это выражение справедливо только в один момент времени. Поэтому его нельзя дифференцировать по времени. Наконец, для малых поворотов, когда

где θ(t) m(t) есть вектор малого поворота.

Выражение (3.14.6) можно, разумеется, получить непосредственно из представлений (3.5.3) и (3.14.2). В самом деле, дифференцируя (3.5.3), получаем

Подставляя это выражение в (3.14.2) и учитывая тождество

(a × E)× = −2 a,

получаем (3.14.6). Выражение (3.14.4) будет удобно во многих случаях, но не всегда. Главный недостаток (3.14.4) состоит в том, что в него входят производные от угла поворота и неподвижного вектора по отдельности. Часто бывает необходимо выразить угловую скорость непосредственно через производную от вектора поворота θ = θ m. Вывод этого представления [21] приведем достаточно подробно. Вычисляя след от обеих частей уравнения Пуассона, по-

лучаем

(tr P)· = tr(ω × P) = −2sinθ θθ · ω.

Принимая во внимание, что

Обратим внимание, что θ в формулах (3.14.11) – (3.14.15) и ниже можно трактовать как модуль вектора поворота θ. Тензор Z(θ), определенный равенством (3.14.15), в дальнейшем будем называть тензором-интегратором. Название объясняется тем, что Z(θ) выполняет роль интегрирующего множителя, переводящего линейную дифференциальную форму ωdt в полный дифференциал dθ вектора поворота θ. Тензор Z(θ) невырожден, ибо его определитель

Он обладает рядом полезных свойств, облегчающих его применение. Отметим некоторые из них. Тензор Z(θ) есть изотропная функция вектора поворота

Если S = P(θ), то из (3.14.17) следует

Кроме того, легко проверить тождество

Используя это тождество, равенство (3.14.14) легко переписать для правой угловой скорости

В терминах вектора поворота левую и правую задачи Дарбу можно переписать в следующих формах

Следует обратить внимание на различие, например, в формулировках левой задачи Дарбу (3.14.1) и (3.14.21). В принципе, эти формулировки эквивалентны. Решив одну из этих задач, мы одновременно решим и другую задачу. На первый взгляд кажется, что формулировка (3.14.1) значительно проще, чем (3.14.21). В самом деле, уравнение (3.14.1) линейно и однородно. Уравнение (3.14.21) существенно нелинейно и неоднородно. Тем не менее, численное,