Zhilin_Fundamental_Laws_Book

по крайней мере, решение задачи (3.14.21) несравнимо проще, нежели решение задачи (3.14.1). В частности, обратим внимание читателя на следующую возможность. Задачу Дарбу (3.14.1) можно простой заменой

Это возможно, поскольку левые угловые скорости для поворотов P(θ) и Q(ϕ) совпадают

Тогда вместо задачи (3.14.21) получаем следующую задачу для вектора

Преимущество последней задачи по сравнению с (3.14.21) в том, что, во– первых, здесь простейшее начальное условие и, во–вторых, очень часто вектор

ϕможно считать малым. Исходный вектор поворота θ можно найти по вектору

ϕи θ0 с помощью формул (3.8.16). Представления (3.14.21) и (3.14.22) можно записать в другой форме

Иногда она бывает полезной.

Этими краткими замечаниями мы здесь и ограничимся. Более детальное описание выходит за рамки данной книги. Приведенные в этом пункте формулы понадобятся нам в дальнейшем при определении потенциальных моментов.

3.15. Угловая скорость композиции поворотов

В приложениях бывает удобно представлять общий поворот P(t) в виде композиции поворотов

Здесь Q1 есть первый поворот, а Q2 — второй поворот. Напомним, что композицию поворотов нельзя понимать так, что сначала, в течение какого–то

интервала времени, производится поворот Q1, а затем, по истечении первого интервала времени, начинает производиться второй поворот Q2. Тензор поворота P(t) — это мгновенное действие, происходящее в момент времени t и состоящее в том, что в момент времени t тензор поворота P(t) поворачивает тело из отсчетного положения в актуальное. В следующий момент времени t + Δt тензор поворота P(t + Δt) переводит тело из отсчетного положения в положение, занимаемое телом в момент времени (t + Δt). Истинное изменение ориентации тела в пространстве описывается не тензором поворота, а его изменением (дифференциалом). Это обстоятельство важно осознать. Полезно поэтому провести аналогию с вектором перемещения u(t)

R(t) = r + u(t).

Вектор u(t) мгновенно переносит тело из отсчетного положения r в актуальное положение R(t). При этом u(t) сам по себе не показывает истинного движения тела, которое, тем не менее, может быть восстановлено по вектору u

При этом d u = vdt, т.е. линейная дифференциальная форма vdt есть полный дифференциал вектора перемещения. Для поворотов ситуация сложнее. Изменение поворота, согласно уравнению Пуассона, определяется через линейную дифференциальную форму ωdt

d P = ωdt × P,

но ωdt не является полным дифференциалом вектора поворота

ωdt = dθ.

По существу именно с этим обстоятельством связаны все усложнения, возникающие при описании поворотов.

Вернемся, однако, к композиции поворотов (3.15.1). Все, сказанное относительно полного поворота P, справедливо и для составляющих поворотов Q1 и Q2. Допустим, нам известны угловые скорости ω1 и ω2 поворотов Q1 и

134 Глава 3. Кинематика: спинорные движения

Теорема: угловая скорость ω полного поворота P, определенного в виде композиции (3.15.1), вычисляется по угловым скоростям ω1 и ω2 составляющих поворотов Q1 и Q2 посредством равенства

Доказательство (3.15.3) вполне элементарно и получается после диффе-

Заменяя здесь производные от тензоров поворота с помощью уравнения Пуассона (3.15.2), получаем

Преобразуем здесь второе слагаемое в правой части

Q2 · (ω1 × Q1) = Q2 · (ω1 × E) · Q1 =

Q2 · (ω1 × E) · QT2 · Q2 · Q1 = [( Q2 · ω1) × E] · Q2 · Q1.

Учитывая это тождество и равенство (3.15.1), вместо (3.15.4) получаем

ω × P = (ω2 + Q2 · ω1) × P.

Умножая это равенство скалярно на PT справа и вычисляя векторные инварианты от обеих частей получившегося равенства, приходим к формуле (3.15.3). Доказательство завершено.

В литературе равенство (3.15.3), точнее его аналог, называют теоремой сложения угловых скоростей. Как уже неоднократно отмечалось, в литературе используется определение угловой скорости, когда в качестве отсчетного положения используется положение в данный момент времени. При таком описании

Q2(τ − t)|τ=t = E

и равенство (3.15.3) переходит в традиционную форму сложения угловых скоростей

Хотя в этом выражении и стоит аргумент t, тем не менее его нельзя дифференцировать по времени, поскольку здесь t есть один фиксированный момент времени. Автор рекомендует не использовать формулы типа (3.15.5) и аналогичные ей выражения, аппелирующие к мгновенному состоянию движения.

Будучи формально правильными, они служат источником многих недоразумений и практически бесполезны. Кроме того, они находятся в трудно устранимом противоречии с интуитивными представлениями. Например, мы знаем, что повороты не коммутируют. Поэтому их угловые скорости должны входить в формулу сложения не равноправно. Это действительно имеет место в (3.15.3), но в (3.15.5) этот факт глубоко замаскирован. В данной книге теорема о сложении угловых скоростей используется исключительно в форме (3.15.3). Из последней вытекает представление для сложения правых угловых скоростей

где

Ω1 = QT1 · ω1, Ω2 = QT2 · ω2.

Из представлений (3.15.3) вытекают формулы для композиции трех и боль-

Упражнение. Доказать (3.15.8).

Ранее мы видели, что угловая скорость в общем случае вычисляется по довольно сложным формулам, представленным в предыдущем параграфе. Все они резко упрощаются, если поворот происходит вокруг фиксированной оси. Тогда угловая скорость вычисляется по простейшей формуле

Поэтому часто бывает полезным общий поворот представить в виде композиции поворотов вокруг фиксированных осей. Рассмотрим, например, композицию поворотов

где m и n — постоянные единичные векторы.

Угловые скорости поворотов Q2(ϕ m) и Q1(ψ n) вычисляются по форму-

которая часто будет использоваться в дальнейшем. Обычно такого рода преобразованиями вообще удается избежать относительно громоздкой операции умножения тензора поворота на вектор. Посмотрим теперь как усложняются вычисления, если хотя бы один из поворотов проводить вокруг меняющейся во времени оси. В соответствии с правилом квазикоммутативности поворотов поворот (3.15.10) можно переписать в виде

Угловая скорость ω поворота Q1(ψ n ) теперь уже должна вычисляться

Поскольку повороты (3.15.10) и (3.15.14) совпадают, то и угловые скорости (3.15.12) и (3.15.17) должны тождественно совпадать, что сразу не очевидно.

Упражнение. Доказать, что выражения (3.15.12) и (3.15.17) приводят к одному и тому же вектору ω(t).

При вычислении производной от вращающегося вектора следует активно пользоваться уравнением Пуассона. Например, для вектора (3.15.15) имеем

˙ = [ (ϕ ) · ]· = ˙ (ϕ ) · = ϕ˙ × (ϕ ) · . n Q2 m n Q2 m n m Q2 m n

Здесь использовано уравнение Пуассона. Вспоминая (3.15.15) окончательно получаем

Если вектор a = const поворачивается тензором поворота общего вида, то вместо (3.15.18) имеем

Если вектор a меняется во времени и, кроме того, поворачивается тензором поворота, то, разумеется, вместо (3.15.19) следует использовать более полное выражение

a (t) = P(t) · a(t) a˙ (t) = P(t) · a˙(t) + ω(t) × a (t). (3.15.20)

Часто последнее выражение удобно представлять в другой форме. При этом следует вспомнить тождество

которое выполняется для любых векторов и любых тензоров поворота. Вводя в рассмотрение правую угловую скорость

ω(t) = P(t) · Ω(t),

равенство (3.15.20) переписываем в виде

В литературе формулы типа (3.15.22) часто трактуют в терминах различного рода наблюдателей. Читатель, уже добившийся более или менее устойчивой визуализации векторных и тензорных объектов, легко сможет самостоятельно интерпретировать смысл формул типа (3.15.22). Тем не менее, в параграфе, посвященном описанию относительных движений, мы обсудим и эти трактовки. Здесь же укажем только, что все величины, входящие в (3.15.22) и другие формулы, заданы в одной и только одной (произвольно выбранной) системе отсчета и, вообще говоря, не нуждаются в каких-то дополнительных трактовках. Замены системы отсчета будут обсуждены позднее в конце этой главы.

Вернемся к вычислению угловой скорости для композиции поворотов. Ранее была доказана теорема (3.8.1) о представлении произвольного тензора поворота в виде композиции трех поворотов вокруг фиксированных и произвольно выбираемых осей. Теорема (3.15.3) позволяет без труда вычислить угловую скорость композиции поворотов (3.8.1)

Здесь единичные векторы m и n выбираются произвольно, но они не зависят от времени. Уравнения Пуассона для поворотов, входящих в (3.15.23), дают

Угловые скорости для составляющих поворотов вычисляются по простейшим формулам. Полная угловая скорость в соответствии с (3.15.8) дается выражением

138 Глава 3. Кинематика: спинорные движения

Уравнение (3.15.24) носит название кинематического уравнения Эйлера. Оно было получено Л. Эйлером для случая m = n и единичного вектора e,

ортогонального m. Величины ˙ , ˙ и носят названия угловых скоростей

ψ ϑ ϕ˙

прецессии, нутации и собственного вращения соответственно. Заметим, что эти названия в общем случае весьма условны, а сами эти величины обретают объективный смысл только при учете специфики как рассматриваемой задачи, так и твердого тела, повороты которого описываются тензором (3.15.23).

3.16. Скорости и ускорения точек твердого тела

Вся информация о кинематических характеристиках движения точек абсолютно твердого тела содержится в основном уравнении кинематики (3.2.6)

где векторы rQ и RQ определяют положение полюса Q в отсчетном и актуальном положениях соответственно, векторы rA и RA определяют положение произвольно выбранной точки A в отсчетном и актуальном положениях соответственно, тензор P(t) определяет поворот абсолютно твердого тела. Чтобы найти распределение скоростей в абсолютно твердом теле достаточно продифференцировать (3.16.1) по времени. Тогда получим

Исключая отсюда производную от тензора поворота с помощью уравнения

получаем

VA(t) = VQ(t) + ω(t) × P(t) · (rA − rQ).

С учетом уравнения (3.16.1) этому соотношению можно придать вид

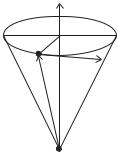
Последнее равенство носит название уравнения Эйлера. Оно позволяет найти скорости всех точек абсолютно твердого тела и допускает ясное геометрическое истолкование для скорости точки A относительно полюса Q (рис. 3.8).

Эта интерпретация упрощается, если полюс Q неподвижен. Тогда в каждый момент времени точка A как бы движется по окружности вокруг оси, натянутой на вектор ω. Следует, впрочем, предостеречь от слишком буквального следования этой интерпретации, поскольку точка A движется по указанной окружности только тогда, когда, во–первых, полюс Q неподвижен и,

ù

VA - VQ

RA - RQ

Q

Рис. 3.8. Интерпретация уравнения Эйлера

во–вторых, вектор угловой скорости ω постоянен. При нарушении любого из этих двух условий фактическое движение точки A происходит по другой траектории, которая может весьма сильно отличаться от упомянутой окружности. Многие книги по механике используют формулу (3.16.4) в качестве определения угловой скорости. Такой подход, разумеется, возможен, но при этом природа угловой скорости и ее связь с поворотами тела оказываются скрытыми. Чтобы получить распределение ускорений в абсолютно твердом теле достаточно продифференцировать (3.16.4) по времени. Тогда получим

WA = WQ + ω˙ × (RA − RQ) + ω × (VA − VQ).

Исключая отсюда скорости с помощью равенства (3.16.4), получаем

Выражение (3.16.5) можно переписать в другой, но эквивалентной, форме

Вектор ω˙ называется вектором угловых ускорений. Тензор второго ранга

будем называть тензором угловых ускорений. Последний можно выразить через левый тензор спина Sl

В заключение этого пункта введем еще два часто используемых в литературе понятия. Рассмотрим тело, имеющее неподвижную точку Q, которую выберем в качестве полюса, причем VQ = 0.

проходящая через неподвижный полюс Q и натянутая на вектор угловой скорости, называется мгновенной осью вращения.

Скалярный параметр λ, входящий в (3.16.9), играет роль расстояния, на которое точка A отстоит от полюса Q. Из выражения (3.16.4) видим, что скорости всех точек, лежащих на мгновенной оси вращения в данный момент времени равны нулю. Иными словами, если тело имеет неподвижную точку Q, то существует такая прямая (3.16.9), что в данный момент времени тело как бы вращается вокруг этой неподвижной прямой. Если тело имеет неподвижную точку, то мгновенная ось вращения всегда существует. Можно распространить понятие мгновенной оси вращения и на другие случаи движения, при которых тело не имеет неподвижной точки. Однако такое расширение возможно не для любых движений.

Определение: мгновенной осью вращения называется прямая, натянутая на вектор угловой скорости и такая, что скорости точек тела, лежащие в данный момент времени на этой прямой, обращаются в нуль.

Выясним при каких условиях, налагаемых на движение тела, мгновенная ось вращения существует. По определению мгновенная ось вращения состоит из точек, скорости которых в данный момент времени равны нулю. Тогда, согласно (3.16.4) для таких точек имеем

Это равенство должно быть справедливым для любого выбора полюса Q, т.е. для всех точек тела. Скалярно умножая (3.16.10) на вектор ω(t), получаем

Поскольку выбор Q произволен, то отсюда следует, что скорости всех точек тела должны быть ортогональны вектору угловой скорости. Этот случай реализуется, например, для так называемых плоских движений твердого тела.

Определение : движение абсолютно твердого тела называется плоским, если скорости всех точек этого тела лежат в плоскостях, ортогональных постоянному единичному вектору e.

Упражнение : доказать, что при плоском движении угловая скорость тела ортогональна плоскостям, в которых лежат векторы скорости, т.е.

ω = ω(t) e.

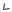x i

Рис. 3.9. Качение цилиндра по плоскости

Итак, будем считать, что условие (3.16.11) выполнено. Тогда (3.16.10) дает нам уравнение для нахождения мгновенной оси вращения. Решая это уравнение, получаем

и натянутую на вектор ω. Мгновенная ось вращения при этом движется в пространстве, хотя скорости точек тела, лежащих в данный момент времени на этой оси, равны нулю. При плоских движениях точка (3.16.13) называется мгновенным центром скоростей. Это понятие широко используется в теории машин и механизмов, но здесь мы его обсуждать не будем.

3.17. Качение цилиндра по плоскости

Простейшим примером плоского движения является качение колеса (цилиндра) по горизонтальной плоскости без проскальзывания. Для решения этой задачи вполне достаточно здравого смысла и мощный аппарат кинематики абсолютно твердого тела в данной задаче не дает особых преимуществ. Тем не менее, аппарат работает и не менее эффективен, чем любой другой подход.

Катящееся по плоскости колесо (поперечное сечение цилиндра) представлено на рис. 3.9.

Одним из величайших открытий в истории человечества было изобретение колеса. Археологические раскопки показывают, что люди далеко не сразу изобрели круглое колесо. Первоначально колеса делались квадратными. При перекатывании углы квадратного колеса обламывались и колеса становились многоугольными, т.е. приближались к круговой форме. Такое колесо считалось