
- •3. Вероятность на дискретном пространстве элементарных исходов. Классическое определение вероятности. Свойства вероятности.
- •4.Элементы комбинаторики и схемы выбора.
- •5. Геометрическая вероятность. Свойства вероятности.
- •7. Формула полной вероятности и формула Байеса.
- •8. Схема незовисимых испытаний Бернулли,формула Бернулли.Общая теорема о повторении опытов.
- •9. Общая теорема о повторении опытов. Наиболее вероятное число успехов в схеме Бернулли. Номер первого успешного испытания.
- •10. Предельные теоремы в схеме Бернулли. Локальная предельная теорема Муавра-Лапласа. Интегральная теорема Муавра-Лапласа.
- •11. Предельные теоремы в схеме Бернулли. Теорема Пуассона. Закон больших чисел в форме Бернулли.
- •12. Случайные величины и распределения вероятностей. Свойства функции распределения вероятностей.
- •13.Классификация случайных величин. Дискретные распределения (примеры основных распределений)
- •I.Дискретные распределения
- •14. .Классификация случайных величин. Абсолютно непрерывные распределения(примеры основных распределений).
- •I. . Абсолютно непрерывные распределения.
- •15.Нормальное распределение и его свойства.
- •16.Основные распределения случайных величин, применяемые в статистике.
- •17.Мат.Ожидание и его свойства.
- •18.Дисперсия и её свойства
- •20 Числовые характеристики системы двух случайных величин.Ковариация.
- •19.Мода,медиана,моменты,ассиметрия,эксцесс
- •21.Числовые характеристики системы двух случайных величин .Коэффициент корреляции.
- •22.Определение случайной последовательности . Определение сходимости по вероятности .Неравенство Маркова. Неравенство Чебышева.
- •24.Центральная предельная теорема для одинаково распределенных независимых слагаемых. (цпт)
- •25.Определение и описание случайного процесса
- •26.Статистические средние характеристики случайных процессов(сп).
- •27.Стационарные случайные процессы(сп)
- •28.Предмет мат. Статистики
- •29.Средние величины
- •30. Показатели вариации, моменты.
- •31. Статистические оценки параметров распределения. Методы нахождения оценок.
- •32.Метод моментов.
- •34.Интервальные оценки.
22.Определение случайной последовательности . Определение сходимости по вероятности .Неравенство Маркова. Неравенство Чебышева.
На практике часто приходится исследовать
последовательность счетного числа СВ
. например, исследуем динамику курса
обмена валюты, в этом случае наблюдается
последовательность ξ1, ξ2 , ξ3…, €R,
где ξnобменный курс вn-ый торговый день. Удобной
моделью для таких случаев явл-ся понятие
случайной последовательности .Случайной
последовательностью { ξn}n=1,2,3… ξn€Rназывается счетное
параметрическое семейство СВ ξ1, ξ2 , ξ3…
параметрnэтого семейства
пробегает множество натуральных чисел.
Основной вопрос, связанный со случайными
последовательностями - это вопрос их
сходимости. В теории вероятности
существует 4 основных вида сходимости:
а) сходимость с вероятностью близкой к
1 б)по вероятности Р в) в среднем порядном
к г) по распределению. Последовательность
СВ { ξn} сходится к случайной
величине ξ по вероятности Р, если для
всех ε› 0 Неравенство Маркова: если Uне
отрицательнььльой СВ
Неравенство Маркова: если Uне
отрицательнььльой СВ
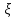 существует
математическое ожидание Мξ
то при любом ε›0
имеет место неравенство Маркова: Р(ξ ‹
ε) ≥1- Мξ/ ε или Р(ξ
существует
математическое ожидание Мξ
то при любом ε›0
имеет место неравенство Маркова: Р(ξ ‹
ε) ≥1- Мξ/ ε или Р(ξ ε)
‹М ξ / ε Пример: средний срок службы
мотора 4года. Оценить снизу вероятность
того, что данный мотор не прослужит
более 20 лет .Решение: пусть СВ ξ- это срок
службы мотора, тогда по условию Мξ
=4 - средний срок службы мотора,
требуется оценить вероятность: Р(ξ
≤20)≥1 – 4/20 =0,8.
ε)
‹М ξ / ε Пример: средний срок службы
мотора 4года. Оценить снизу вероятность
того, что данный мотор не прослужит
более 20 лет .Решение: пусть СВ ξ- это срок
службы мотора, тогда по условию Мξ
=4 - средний срок службы мотора,
требуется оценить вероятность: Р(ξ
≤20)≥1 – 4/20 =0,8.
Неравенство Чебышева: для всех ε›0 и
любой СВ ξ, дисперсия которой конечна(
то есть Dξ<∞) имеет
место неравенство Чебышева Р(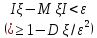 ),или
Р(
),или
Р(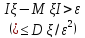 Пример:
средняя длина детали 50см, а дисперсия
0,1 пользуясь неравенством Чебышева
оценить вероятность того, что случайно
взятая деталь окажется по длине не
меньше 49,5см и не больше50,5 см. Решение:
пусть СВ
Пример:
средняя длина детали 50см, а дисперсия
0,1 пользуясь неравенством Чебышева
оценить вероятность того, что случайно
взятая деталь окажется по длине не
меньше 49,5см и не больше50,5 см. Решение:
пусть СВ -это длина случайно взятой детали , по
условию Мξ=50, Д
-это длина случайно взятой детали , по
условию Мξ=50, Д =0,1
тогдаσξ = корень из 0,1 .. Требуется
оценить следующую вероятность
Р(49,5‹ξ‹50,5)=Р(
=0,1
тогдаσξ = корень из 0,1 .. Требуется
оценить следующую вероятность
Р(49,5‹ξ‹50,5)=Р( )=0,6.
)=0,6.
23.неравенство Маркова. Неравенство Чебышева. ЗБЧ и условие его выполнения.
Неравенство Маркова: еслиUне
отрицательной СВ
 существует
математическое ожидание Мξ
то при любом ε›0
имеет место неравенство Маркова: Р(ξ ‹
ε) ≥1- Мξ/ ε или Р(ξ
существует
математическое ожидание Мξ
то при любом ε›0
имеет место неравенство Маркова: Р(ξ ‹
ε) ≥1- Мξ/ ε или Р(ξ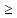 ε)
‹М ξ / ε Пример: средний срок службы
мотора 4года. Оценить снизу вероятность
того, что данный мотор не прослужит
более 20 лет .Решение: пусть СВ ξ- это срок
службы мотора, тогда по условию Мξ
=4 - средний срок службы мотора,
требуется оценить вероятность Р(ξ ≤20)≥1
– 4/20 =0,8.
ε)
‹М ξ / ε Пример: средний срок службы
мотора 4года. Оценить снизу вероятность
того, что данный мотор не прослужит
более 20 лет .Решение: пусть СВ ξ- это срок
службы мотора, тогда по условию Мξ
=4 - средний срок службы мотора,
требуется оценить вероятность Р(ξ ≤20)≥1
– 4/20 =0,8.
Неравенство Чебышева: для всех ε›0 и
любой СВ ξ, дисперсия которой конечна(
то есть Dξ<∞) имеет
место неравенство Чебышева Р(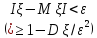 ),или
Р(
),или
Р( Пример:
средняя длина детали 50см, а дисперсия
0,1 пользуясь неравенством Чебышева
оценить вероятность того, что случайно
взятая деталь окажется по длине не
меньше 49,5см и не больше50,5 см. Решение:
пусть СВ
Пример:
средняя длина детали 50см, а дисперсия
0,1 пользуясь неравенством Чебышева
оценить вероятность того, что случайно
взятая деталь окажется по длине не
меньше 49,5см и не больше50,5 см. Решение:
пусть СВ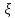 -это длина случайно взятой детали , по
условию Мξ=50, Д
-это длина случайно взятой детали , по
условию Мξ=50, Д =0,1
тогда σξ = корень из 0,1 .. Требуется
оценить следующую вероятность
Р(49,5‹ξ‹50,5)=Р(
=0,1
тогда σξ = корень из 0,1 .. Требуется
оценить следующую вероятность
Р(49,5‹ξ‹50,5)=Р(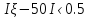 )=0,6.
)=0,6.
ЗБЧ и условие его выполнения .
Закон больших чисел - это обобщенное
название нескольких теорем, из которых
следует, что при неограниченном увеличении
числа испытаний средние величины
стремятся к некоторым постоянным. По
формуле выглядит это так: 1/n*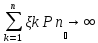 1/n*
1/n*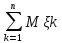
То есть под ЗБЧ понимается свойство устойчивости массовых явлений состоящее в том что средний результат действия большого числа случайных явлений перестает быть случайным и может быть предсказуем с достаточной определенностью.
Теорема Чебышева
Пусть ξ1, ξ2 , ξ3- это последовательность
независимых СВ, имеющих конечные
дисперсии, ограниченные одной и той же
постоянной С, то есть Dξk≤C,k=1,2,3... Тогда какого бы ни
было положительное число , справедливо: Р(l 1/n*
, справедливо: Р(l 1/n*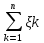 -1/n*
-1/n*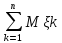 l<
ε)≥1-D(
l<
ε)≥1-D(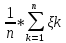 )/ε2=1-D(
)/ε2=1-D(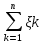 )/n2ε2=1-
)/n2ε2=1-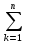 D(
D( )/n2ε2≥1-
)/n2ε2≥1- /n2ε2=1-nC/n2ε2=1-C/nε2.
/n2ε2=1-nC/n2ε2=1-C/nε2.
Отсюда следует, что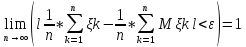 (так
как из полученной оценки мы имеем Р(l
1/n*
(так
как из полученной оценки мы имеем Р(l
1/n* -1/n*
-1/n*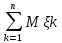 l<
ε)≥1 приn→∞, то тем
самым это означает Р(l
1/n*
l<
ε)≥1 приn→∞, то тем
самым это означает Р(l
1/n*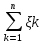 -1/n*
-1/n*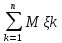 l<
ε) →1 приn→∞.
l<
ε) →1 приn→∞.
Пример: сколько раз нужно измерить
данную величину, истинное значение
которой = а, чтобы с вероятностью не
меньшей 95% можно было утверждать, что
среднее арифметическое значение этих
измерений отличается от а по абсолютной
величине меньше чем на 2,если среднее
квадратичное отклонение каждого из
измерений меньше 10. Решение: пусть СВ
ξiэто результат і-ого
измерения, по условию М ξi=aσξi<10,Dξi<100,….,n- ? по вероятности Р (l
1/n*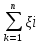 -al<
2) ≥0.95 . В данном примере Св ξiодинаково распределены и 1/n*
-al<
2) ≥0.95 . В данном примере Св ξiодинаково распределены и 1/n* =1/n*
=1/n*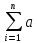 =a.Aс другой
стороны дольно выполняются неравенство
Р(l 1/n*
=a.Aс другой
стороны дольно выполняются неравенство
Р(l 1/n*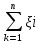 -al<
2)≥1-100/n*2^2, неравенство во
всяком случае будет выполняться , если
1-100/n*2^2≥0,95, →n=500(
то есть надо провести более 500 опытов,
чтобы с вероятностью в 95% быть уверенным
, что среднее арифметическое значение
отличается меньше чем на 2).
-al<
2)≥1-100/n*2^2, неравенство во
всяком случае будет выполняться , если
1-100/n*2^2≥0,95, →n=500(
то есть надо провести более 500 опытов,
чтобы с вероятностью в 95% быть уверенным
, что среднее арифметическое значение
отличается меньше чем на 2).
Теорема бернулли : Пусть m — число наступлений события A в k независимых (попарно) испытаниях, и p есть вероятность наступления события A в каждом из испытаний. Тогда при любом ε>0 справедливо неравенство: P{lm/k-pl≥ε}≤p*(1-p)/kε2 .
